Константная функция
Константная функция (также постоянная функция) — функция, которая для любого элемента из области определения возвращает одно и то же заданное значение. Заданная отображением [math]\displaystyle{ f\colon X \to Y }[/math] функция [math]\displaystyle{ f }[/math] является константной, если для любых элементов [math]\displaystyle{ x_1,x_2 \in X }[/math] выполняется равенство: [math]\displaystyle{ f(x_1)=f(x_2)=y }[/math], где [math]\displaystyle{ y \in Y }[/math]. Это означает, что множество значений функции состоит из одного единственного элемента.
Константная числовая функция [math]\displaystyle{ f\colon \R \to \R }[/math], заданная на множестве действительных чисел, является целой рациональной функцией нулевой степени или линейной функцией, график которой проходит параллельно оси абсцисс. Эта функция имеет уравнение вида [math]\displaystyle{ f(x)=a }[/math], где [math]\displaystyle{ a \in \R }[/math]. Такая функция является чётной на всей области определения, и поэтому её график обладает осевой симметрией относительно оси ординат. Производной любой константной функции [math]\displaystyle{ f(x)=a }[/math] является нулевая функция [math]\displaystyle{ f'(x)=0 }[/math], которая является специальным случаем константных функций.
Преобразование Фурье константной функции [math]\displaystyle{ f(x)=1 }[/math] даёт дельта-функцию.
Иллюстрации
-
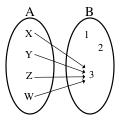
Константное отображение множеств
-
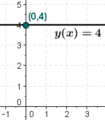
в декартовой системе координат на плоскости
-
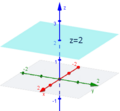
в декартовой системе в пространстве
См. также
Ссылки
- MathWorld: Constant Function (англ.)