Полусумматор

Полусумма́тор — комбинационная логическая схема, имеющая два входа и два выхода (двухразрядный сумматор, бинарный сумматор). Полусумматор позволяет вычислять сумму A+B, где A и B — это разряды (биты) обычно двоичного числа, при этом результатом будут два бита S и C, где S — это бит суммы по модулю 2, а C — бит переноса.
Существуют сумматоры и полусумматоры работающие не в двоичной логике.
Отличается от полного сумматора тем, что не имеет входа переноса из предыдущего разряда. Для построения полного сумматора необходимо иметь дополнительный вход переноса из предыдущего разряда, таким образом, полный сумматор имеет 3 входа.
Двоичный полный сумматор строится из двух полусумматоров и логического элемента 2ИЛИ, именно поэтому рассматриваемая схема называется полусумматором.
Полусумматоры используется для построения полных сумматоров.
История
- 1939 год — Джордж Штибиц (Georg Stibits) из компании Bell Laboratories создал первый двоичный полусумматор «Model K Аdder» на двух электромеханических реле[1].
- 1958 год — в МГУ (мехмат) Н. П. Брусенцов построил первую электронную троичную ЭВМ «Сетунь» с первым электронным троичным полусумматором[2].
Двоичный полусумматор


Двоичный полусумматор может быть определён тремя способами:
- табличным, в виде таблиц истинности,
- аналитическим, в виде формул (СДНФ),
- графическим, в виде логических схем.
Так как формулы и схемы могут преобразовываться в соответствии с алгеброй логики, то, одной таблице истинности двоичного полусумматора могут соответствовать множества различных формул и схем. Поэтому, табличный способ определения двоичного полусумматора является основным.
Двоичный полусумматор формирует две бинарные (двухоперандные) двоичные логические функции: это сумма по модулю два, иначе эта функция называется ИСКЛЮЧАЮЩЕЕ ИЛИ (XOR) — формирует бит суммы S и функция И (AND) - формирует бит переноса C.
- S
| 1 | 1 | 0 |
|---|---|---|
| 0 | 0 | 1 |
| 0 | 1 |
- C
| 1 | 0 | 1 |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 |
или в другом виде:
| x0=A | 1 | 0 | 1 | 0 | ||
|---|---|---|---|---|---|---|
| x1=B | 1 | 1 | 0 | 0 | Название действия (функции) | Номер функции |
| S | 0 | 1 | 1 | 0 | Бит суммы по модулю 2 | F2,6 |
| C | 1 | 0 | 0 | 0 | Бит переноса | F2,8 |
- Ненулевой перенос образуется в 1-м случае из 4-х.
СДНФ суммы по модулю 2:
- [math]\displaystyle{ S=\mathbf{f}(x_1,x_0)=(\overline{x_1}\cdot{x_0})\vee({x_1}\cdot\overline{x_0}) }[/math]
СДНФ бита переноса:
- [math]\displaystyle{ C=\mathbf{f}(x_1,x_0)={x_1}\cdot{x_0} }[/math]
Полусумматор Штибица «Model K Аdder»
Демонстрационный полусумматор Штибица «Model K Аdder» используется в учебных целях и состоит: из двух последовательно соединённых гальванических элементов, по 1,5 Вольта каждый, с суммарным напряжением 3 Вольта, двух кнопок для ввода двух битов аргументов A и B, двух электромагнитных реле, выполняющих бинарную двоичную логическую функцию сложения по модулю 2 и бинарную двоичную логическую функцию бита переноса при двоичном сложении, и двух лампочек накаливания с напряжением 3 Вольта для индикации бита суммы по модулю 2 (S) и бита переноса (C)[1]
Троичный полусумматор
Так как существуют две троичных системы счисления — несимметричная, в которой в разряде переноса не бывает значения больше «1» и симметричная (Фибоначчи), в которой в разряде переноса возможны все три состояния трита, и, как минимум, три физических реализации троичных систем — трёхуровневая однопроводная, двухуровневая двухпроводная (BCT) и двухуровневая трёхбитная одноединичная, то и троичных полусумматоров может быть большое множество.
Троичный полусумматор в несимметричной троичной системе счисления представляет собой объединение двух бинарных троичных логических функций — «сложение по модулю 3» и «разряд переноса при троичном сложении».
- S
| 2 | 2 | 0 | 1 |
|---|---|---|---|
| 1 | 1 | 2 | 0 |
| 0 | 0 | 1 | 2 |
| 0 | 1 | 2 |
- C
| 2 | 0 | 1 | 1 |
|---|---|---|---|
| 1 | 0 | 0 | 1 |
| 0 | 0 | 0 | 0 |
| 0 | 1 | 2 |
или в другом виде:
| x1=x | 2 | 2 | 2 | 1 | 1 | 1 | 0 | 0 | 0 | ||
|---|---|---|---|---|---|---|---|---|---|---|---|
| x0=y | 2 | 1 | 0 | 2 | 1 | 0 | 2 | 1 | 0 | Название действия (функции) | Номер функции |
| S | 1 | 0 | 2 | 0 | 2 | 1 | 2 | 1 | 0 | Трит суммы по модулю 3 | |
| C | 1 | 1 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | Трит переноса |
Троичный полусумматор в симметричной троичной системе счисления является также и полувычитателем и представляет собой объединение двух бинарных троичных логических функций — «младший разряд (трит) суммы-разности» и «старший разряд (трит) суммы-разности (разряд переноса при сложении-вычитании в троичной симметричной системе счисления)».

- S
| +1 | 0 | +1 | -1 |
|---|---|---|---|
| 0 | -1 | 0 | +1 |
| -1 | +1 | -1 | 0 |
| -1 | 0 | +1 |
- C
| +1 | 0 | 0 | +1 |
|---|---|---|---|
| 0 | 0 | 0 | 0 |
| -1 | -1 | 0 | 0 |
| -1 | 0 | +1 |
или в другом виде:
| x1=x | 1 | 1 | 1 | 0 | 0 | 0 | 7 | 7 | 7 | ||
|---|---|---|---|---|---|---|---|---|---|---|---|
| x0=y | 1 | 0 | 7 | 1 | 0 | 7 | 1 | 0 | 7 | Название действия (функции) | Номер функции |
| S | 7 | 1 | 0 | 1 | 0 | 7 | 0 | 7 | 1 | Младший трит суммы | F710107071=F-4160 |
| C | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 7 | Старший трит суммы (трит переноса) | F100000007=F6560 |
Цифра «7» здесь обозначает «-1»
Ненулевой перенос образуется в 2-х случаях из 9-ти.
Троичный трёхуровневый полусумматор описан в[3].
Троичный двухбитный двухпроводный бинарный (двухоперандный) одноразрядный (BCT) полусумматор, работающий в несимметричной троичной системе счисления приведён в[4], в разделе BCT Addition, в подразделе (f) Circuit diagram и, с ошибочным названием «двухразрядный BCT сумматор», в[5] на рисунке.
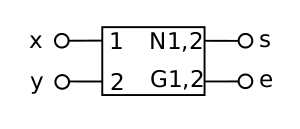
На рисунке справа приведена схема троичного несимметричного полусумматора в трёхбитной одноединичной системе троичных логических элементов, описанного в[6].
Троичный зеркально-симметричный одноразрядный полусумматор описан в[7].
Десятичный полусумматор
Состоит из двух таблиц размером 10х10. Первая таблица — суммы по модулю 10, вторая таблица — единицы переноса при бинарном (двухоперандном) десятичном сложении[8].
- S
| 9 | 9 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
|---|---|---|---|---|---|---|---|---|---|---|
| 8 | 8 | 9 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 7 | 7 | 8 | 9 | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
| 6 | 6 | 7 | 8 | 9 | 0 | 1 | 2 | 3 | 4 | 5 |
| 5 | 5 | 6 | 7 | 8 | 9 | 0 | 1 | 2 | 3 | 4 |
| 4 | 4 | 5 | 6 | 7 | 8 | 9 | 0 | 1 | 2 | 3 |
| 3 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 0 | 1 | 2 |
| 2 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 0 | 1 |
| 1 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 0 |
| 0 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
- C
| 9 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
|---|---|---|---|---|---|---|---|---|---|---|
| 8 | 0 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| 7 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| 6 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 1 | 1 |
| 5 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 1 |
| 4 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 |
| 3 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 |
| 2 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 |
| 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
Шестнадцатиричный полусумматор
Состоит из двух таблиц размером 16х16. Первая таблица — суммы по модулю 16, вторая таблица — единицы переноса при бинарном (двухоперандном) шестнадцатиричном сложении.
- S
| F | F | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | A | B | C | D | E |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| E | E | F | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | A | B | C | D |
| D | D | E | F | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | A | B | C |
| C | C | D | E | F | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | A | B |
| B | B | C | D | E | F | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | A |
| A | A | B | C | D | E | F | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| 9 | 9 | A | B | C | D | E | F | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 8 | 8 | 9 | A | B | C | D | E | F | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 7 | 7 | 8 | 9 | A | B | C | D | E | F | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
| 6 | 6 | 7 | 8 | 9 | A | B | C | D | E | F | 0 | 1 | 2 | 3 | 4 | 5 |
| 5 | 5 | 6 | 7 | 8 | 9 | A | B | C | D | E | F | 0 | 1 | 2 | 3 | 4 |
| 4 | 4 | 5 | 6 | 7 | 8 | 9 | A | B | C | D | E | F | 0 | 1 | 2 | 3 |
| 3 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | A | B | C | D | E | F | 0 | 1 | 2 |
| 2 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | A | B | C | D | E | F | 0 | 1 |
| 1 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | A | B | C | D | E | F | 0 |
| 0 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | A | B | C | D | E | F |
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | A | B | C | D | E | F |
- C
| F | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| E | 0 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| D | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| C | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| B | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| A | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| 9 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| 8 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| 7 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| 6 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 1 | 1 |
| 5 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 1 |
| 4 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 |
| 3 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 |
| 2 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 |
| 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | A | B | C | D | E | F |
См. также
Примечания
- ↑ 1,0 1,1 http://www.computerhistory.org/collections/accession/XD127.80 Computer History Museum
- ↑ http://www.computer-museum.ru/histussr/setun2.htm Архивная копия от 19 июля 2013 на Wayback Machine Малая автоматическая цифровая машина «Сетунь». Н. П. Брусенцов, Е. А. Жоголев, В. В. Веригин, С. П. Маслов, А. М. Тишулина
- ↑ http://spanderashvili.narod.ru/PA.pdf Архивная копия от 14 февраля 2019 на Wayback Machine Астраханский Государственный Технический Университет, Кафедра «Автоматизированные системы обработки информации и управления», Курсовая работа по дисциплине «Объектно-ориентированное программирование» по специальности 220200 «Автоматизированные системы обработки информации и управления», Выполнили Морозов А. В., Спандерашвили Д. В., Алтуфьев М. Ю., Проверил к.т. н., доц. Лаптев В. В., Гл. XXIV Троичный полусумматор. Астрахань-2001 г.
- ↑ http://www.dcs.gla.ac.uk/~simon/teaching/CS1Q-students/systems/tutorials/tut3sol.pdf Архивная копия от 21 января 2022 на Wayback Machine CS1Q Computer Systems
- ↑ http://314159.ru/kushnerov/kushnerov1.pdf Архивная копия от 7 октября 2013 на Wayback Machine Троичная цифровая техника. Ретроспектива и современность
- ↑ Троичный трёхбитный (3B BCT) полусумматор в троичной несимметричной системе счисления. Дата обращения: 20 ноября 2015. Архивировано 20 ноября 2015 года.
- ↑ Компьютеры Фибоначчи. Троичное зеркально-симметричное сложение и вычитание (недоступная ссылка). Дата обращения: 28 сентября 2010. Архивировано 30 октября 2010 года.
- ↑ М. А. Карцев. Арифметика цифровых машин. Главная редакция физико-математической литературы издательства «Наука», 1969, 576 стр. 2. Сумматоры и другие схемы для выполнения элементарных операций. 2.3. Одноразрядные комбинационные сумматоры для десятичной и других систем счисления. Стр.71. Дата обращения: 3 апреля 2013. Архивировано 2 апреля 2013 года.