Поверхность Безье

Поверхность Безье — параметрическая поверхность, используемая в компьютерной графике, автоматизированном проектировании, и моделировании. Это одно из распространённых пространственных обобщений кривой Безье.
При кусочном моделировании (patch modeling) для задания и изменения формы куска, представляющего собой пространственную решетку из сплайнов или многоугольников, применяется сеть контрольных точек. Эти точки управления, также известные как контрольные вершины (control vertices — CV) оказывают на гибкую поверхность куска подобное магнитному влияние, при котором поверхность растягивается в том или ином направлении. Кроме того, куски можно и дальше подразделять на элементы для достижения большего разрешения и «сшивать» друг с другом, тем самым создавая сложные объёмные поверхности. Так же, как и сплайновые, кусочные модели используются при создании органических форм.
Уравнение поверхности
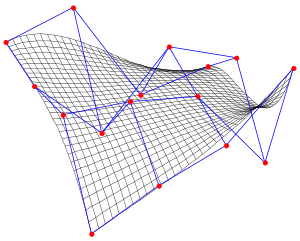
Поверхность Безье порядка [math]\displaystyle{ (n,m) }[/math] задаётся [math]\displaystyle{ (n+1)\cdot(m+1) }[/math] контрольными точками [math]\displaystyle{ \mathbf{P}_{i,j} }[/math]. Точки поверхности рассчитываются следующей параметризацией:
- [math]\displaystyle{ \mathbf{p}(u, v) = \sum_{i=0}^n \sum_{j=0}^m B_i^n(u) \; B_j^m(v) \; \mathbf{P}_{i,j} }[/math],
где [math]\displaystyle{ u,v\in(0,1) }[/math], а [math]\displaystyle{ B }[/math] — многочлены Бернштейна:
- [math]\displaystyle{ B_i^n(u) = {n \choose i} \; u^i (1-u)^{n-i} = \frac{n!}{i! (n-i)!} \; u^i (1-u)^{n-i} }[/math]
Наиболее часто используются бикубические поверхности Безье [math]\displaystyle{ (n=m=3) }[/math], задающиеся шестнадцатью контрольными точками.
Литература
- Роджерс Д., Адамс Дж. Математические основы машинной графики. — М.: Мир, 2001. — ISBN 5-03-002143-4.
- BEZIER_SURFACE. Routines for Bezier Surface Information Архивная копия от 28 сентября 2010 на Wayback Machine (англ.) — Библиотека функций Matlab и Fortran, позволяющая исследовать свойства Безье-поверхностей. Распространяется в соответствии с лицензией LGPL.