Опыт Хейнса — Шокли

Установка для проведения опыта Хейнса, 1948

Форма сигнала на зонде-коллекторе. Узкий первый импульс совпадает по времени с передним фронтом импульса генератора.

Опыт Хейнса — Шокли — классический физический эксперимент, впервые доказавший существование тока неосновных носителей (дырочной проводимости в полупроводнике n-типа) в полупроводниках и позволивший измерить основные свойства дырок — скорость дрейфа и скорость диффузии. Опыт был поставлен Ричардом Хейнсом в лаборатории полупроводников Bell Labs в феврале 1948 года и теоретически объяснён Уильямом Шокли. Статья Хейнса и Шокли с описанием опыта была опубликована в 1949 году в Physical Review.

Описание эксперимента

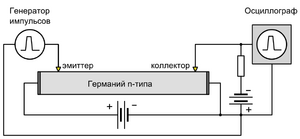
В своём первом опыте Хейнс использовал стержень из германия с электронным типом проводимости длиной 25 мм и поперечным сечением около 8 мм². Концы стержня были подключены к батарее, порождавшей в стержне ток электронов (справа налево, из минуса — в плюс). Левый по схеме скользящий контакт-зонд (аналог эмиттера точечного транзистора) был подключен к генератору коротких импульсов тока положительной полярности, правый контакт-зонд (аналог коллектора) был подключен к осциллографу, синхронизируемому генератором в ждущем режиме.

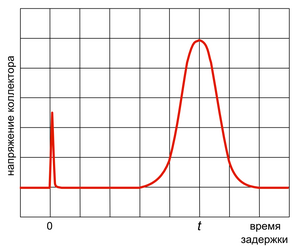
Если бы стержень был изготовлен не из полупроводника, а из металла, то в нём бы протекал только ток электронов, и наблюдаемый на экране осциллографа импульс совпадал бы по времени с импульсом тока генератора. Но в эксперименте с германиевым стержнем на экране осциллографа наблюдалось два импульса. Первый из них, узкий импульс тока замыкания, совпадал по времени с передним фронтом импульса генератора, второй (импульс дырочного тока) значительно оставал от импульса генератора и имел размытую, колоколообразную форму. Задержка и ширина второго импульса увеличивались с ростом расстояния между зондами. При изменении полярности батареи второй (размытый) импульс не наблюдался.

Шокли объяснил увиденное тем, что эмиттер инжектирует в стержень не электроны, а дырки. Инжектированные дырки дрейфуют в сторону отрицательного полюса батареи (вправо) со скоростью, прямо пропорциональной напряжённости поля в полупроводнике. Время дрейфа между двумя зондами пропрорционально расстоянию между ними. Одновременно, хаотичные тепловые перемещения дырок (диффузия) приводят к размыванию формы импульса. За время дрейфа группы инжектированных дырок между двумя зондами «она может распространиться по всему поперечному сечению образца и вдоль него на величину, кратную нескольким его диаметрам». При изменении полярности батареи дырки движутся в сторону, противоположную коллектору (влево от эмиттера) — поэтому расположенный справа от эмиттера коллектор «не видит» импульса дырочного тока.

Измерения, проведённые на кремнии и германии разных типов проводимости, подтвердили положение статистической физики о том, что подвижность μ (зависимость скорости дрейфа от напряжённости поля) и электронов, и дырок связана с коэффициентом диффузии D простым отношением:

D = μ (kT/q), где kT/q — электрический потенциал, соответствующий средней тепловой энергии электрона, и равный 25 мВ при комнатной температуре.

Смысл его таков, что электрон, участвующий в беспорядочном тепловом движении, способен преодолеть потенциальный барьер с высотой, равной в среднем 0,025 В. Другими словами, 0,025 В — это электрический потенциал, соответствующий средней тепловой энергии электрона. То обстоятельство, что указанное отношение равно 0,025 В, показывает, что заряд носителей, дрейф и диффузия которых исследуются в опыте Хайнса, равен по величине заряду электрона.

Уравнения для токов

Чтобы увидеть эффект, рассмотрим полупроводник n-типа длиной d. Нас будут интересовать такие характеристики носителей тока как подвижность, коэффициент диффузии и время релаксации. Удобно рассматривать одномерную задачу (векторы опущены для простоты).

Уравнения для электронного и дырочного токов записываются в виде:

[math]\displaystyle{ j_e=-\mu_n n E-D_n \frac{\partial n}{\partial x} }[/math]

[math]\displaystyle{ j_p=+\mu_p p E-D_p \frac{\partial p}{\partial x} }[/math]

где j_e(p) — плотность тока для электронов (e) и дырок(p), μ_e(p) — соответствующие подвижности, E — электрическое поле, n и p — плотности носителей заряда, D_e(p) — коэффициенты диффузии, x — независимая координата. Первое слагаемое в каждом уравнении линейное по электрическому полю соответствует дрейфовой составляющей полного тока, а второе — пропорциональное градиенту концентрации — диффузии.

Вывод

Рассмотрим уравнение непрерывности:

[math]\displaystyle{ \frac{\partial n}{\partial t}=\frac{-(n-n_0)}{\tau_n}-\frac{\partial j_e}{\partial x} }[/math]

[math]\displaystyle{ \frac{\partial p}{\partial t}=\frac{-(p-p_0)}{\tau_p}-\frac{\partial j_p}{\partial x}. }[/math]

Индекс 0 указывает равновесные концентрации. Электроны и дырки рекомбинируют с временем жизни носителей τ.

Определим

[math]\displaystyle{ p_1=p-p_0\,,\quad n_1=n-n_0 }[/math]

поэтому приведённая выше система уравнений преобразуется к виду:

[math]\displaystyle{ \frac{\partial p_1}{\partial t}=D_p \frac{\partial^2 p_1}{\partial x^2}-\mu_p p \frac{\partial E}{\partial x}- \mu_p E \frac{\partial p_1}{\partial x}-\frac{p_1}{\tau_p} }[/math]

[math]\displaystyle{ \frac{\partial n_1}{\partial t}=D_n \frac{\partial^2 n_1}{\partial x^2}+\mu_n n \frac{\partial E}{\partial x}+ \mu_n E \frac{\partial n_1}{\partial x}-\frac{n_1}{\tau_n} }[/math]

В простейшем приближении, можно считать электрическое поле постоянным между левым и правым электродами и пренебречь ∂E/∂x, однако, электроны и дырки диффундируют с разными скоростями, и материал имеет локальный электрический заряд, вызывая неоднородное распределение электрического поля, которое может быть рассчитано из закона Гаусса:

[math]\displaystyle{ \frac{\partial E}{\partial x}= \frac{\rho}{\epsilon \epsilon_0}=\frac{e_0 ((p-p_0)-(n-n_0))}{\epsilon \epsilon_0} = \frac{e_0 (p_1-n_1)}{\epsilon \epsilon_0} }[/math]

где ε — диэлектрическая проницаемость полупроводника, ε₀ — диэлектрическая проницаемость вакуума, ρ — плотность заряда, и e₀ — элементарный заряд.

сделаем замену переменных:

[math]\displaystyle{ p_1 = n_\text{mean}+\delta\,,\quad n_1 = n_\text{mean}-\delta\,, }[/math]

и пусть δ будет гораздо меньше, чем [math]\displaystyle{ n_\text{mean} }[/math]. Два исходных уравнений запишутся в виде:

[math]\displaystyle{ \frac{\partial n_\text{mean}}{\partial t}=D_p \frac{\partial^2 n_\text{mean}}{\partial x^2}-\mu_p p \frac{\partial E}{\partial x}- \mu_p E \frac{\partial n_\text{mean}}{\partial x}-\frac{n_\text{mean}}{\tau_p} }[/math]

[math]\displaystyle{ \frac{\partial n_\text{mean}}{\partial t}=D_n \frac{\partial^2 n_\text{mean}}{\partial x^2}+\mu_n n \frac{\partial E}{\partial x}+ \mu_n E \frac{\partial n_\text{mean}}{\partial x}-\frac{n_\text{mean}}{\tau_n} }[/math]

Используя соотношение Эйнштейна [math]\displaystyle{ \mu=e\beta D }[/math], где β — величина обратная произведению температуры и постояннай Больцмана, эти два уравнения можно объединить:

[math]\displaystyle{ \frac{\partial n_\text{mean}}{\partial t}=D^* \frac{\partial^2 n_\text{mean}}{\partial x^2}- \mu^* E \frac{\partial n_\text{mean}}{\partial x}-\frac{n_\text{mean}}{\tau^*}, }[/math]

где для D*, μ* and τ* справедливо:

[math]\displaystyle{ D^*=\frac{D_n D_p(n+p)}{p D_p+nD_n} }[/math], [math]\displaystyle{ \mu^*=\frac{\mu_n\mu_p(n-p)}{p\mu_p+n\mu_n} }[/math] and [math]\displaystyle{ \frac{1}{\tau^*}=\frac{p\mu_p\tau_p+n\mu_n\tau_n}{\tau_p\tau_n(p\mu_p+n\mu_n)}. }[/math]

Учитывая, n >> p или p → 0 (что справедливо для полупроводников только с малой концентрацией неосновных носителей), D* → D_p, μ* → μ_p и 1/τ* → 1/τ_p. Полупроводник ведет себя, как если бы только дырки двигались в нём.

Окончательное выражение для носителей:

[math]\displaystyle{ n_\text{mean}(x,t)=A \frac{1}{\sqrt{4\pi D^* t}} e^{-t/\tau^*} e^{-\frac{(x+\mu^*Et-x_0)^2}{4D^*t}} }[/math]

Его можно интерпретировать как дельта-функцию, которая создается сразу же после импульса. Дырки затем начать двигаться к противоположному электроду, где их детектируют. Сигнал при этом приоретает форму гауссиана.

Параметры μ, D и τ можно получить из анализа формы сигнала.

[math]\displaystyle{ \mu^*=\frac{d}{E t_0}\,, }[/math]

[math]\displaystyle{ D^*=(\mu^* E)^2 \frac{(\delta t)^2}{16 t_0}\,, }[/math]

где d — расстояние дрейфа за время t₀, и δt — ширина импульса.

Источники

• Haynes, R.; Shockley, W. Investigation of Hole Injection in Transistor Action // Physical Review. — 1949. — Т. 75. — С. 691—699.
• Шокли, В. Физика транзисторов // Успехи физических наук. — 1958. — Т. LXIV, № 1. — С. 155—192.