Неравенство Йенсена

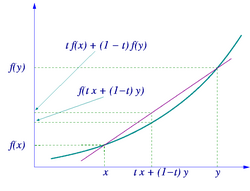
Нера́венство Йе́нсена — неравенство, введённое Иоганом Йенсеном и тесно связанное с определением выпуклой функции.

Формулировки

Конечный случай

Пусть функция [math]\displaystyle{ f\left(x\right) }[/math] является выпуклой на некотором промежутке [math]\displaystyle{ \mathcal X }[/math] и числа [math]\displaystyle{ \ q_1,q_2,\ldots,q_n }[/math] таковы, что

[math]\displaystyle{ \ q_1,q_2,\ldots,q_n\gt 0 }[/math] и [math]\displaystyle{ \ q_{1}+q_2+\ldots+q_n=1 }[/math].

Тогда каковы бы ни были числа [math]\displaystyle{ \ x_1,x_2,\ldots,x_n }[/math] из промежутка [math]\displaystyle{ \mathcal X }[/math], выполняется неравенство:

[math]\displaystyle{ f(q_1x_1+q_2x_2+\ldots+q_nx_n)\le q_1f(x_1)+q_2f(x_2)+\ldots+q_nf(x_n) }[/math]

или

[math]\displaystyle{ f \left( \sum_{i=1}^{n} q_i x_i \right) \le \sum_{i=1}^{n} q_i f (x_i) }[/math].

Замечания:

Если функция [math]\displaystyle{ \ f(x) }[/math] вогнута (выпукла вверх), то знак в неравенстве меняется на противоположный.
Сам Иоган Йенсен исходил из более частного соотношения, а именно

[math]\displaystyle{ f \left( \frac {x_1+x_2}{2} \right) \le \frac {f(x_1)+f(x_2)} {2} }[/math], оно отвечает случаю [math]\displaystyle{ q_1=q_2=\frac {1}{2} }[/math].

Доказательство

Доказательство проводится методом математической индукции.

Для [math]\displaystyle{ \ n=2 }[/math] неравенство следует из определения выпуклой функции.
Допустим, что оно верно для какого-либо натурального числа [math]\displaystyle{ \ n }[/math], докажем, что оно верно и для [math]\displaystyle{ \ n+1 }[/math], то есть

[math]\displaystyle{ f(q_1x_1+q_2x_2+\ldots+q_nx_n+q_{n+1}x_{n+1})\le q_1f(x_1)+q_2f(x_2)+\ldots+q_nf(x_n)+q_{n+1}f(x_{n+1}) }[/math].

С этой целью, заменим слева сумму двух последних слагаемых [math]\displaystyle{ \ q_nf(x_n)+q_{n+1}f(x_{n+1}) }[/math] одним слагаемым

[math]\displaystyle{ (q_n+q_{n+1}) \left( \frac {q_n}{q_n+q_{n+1}} f(x_n)+ \frac {q_{n+1}}{q_n+q_{n+1}} f(x_{n+1}) \right) }[/math];

это даст возможность воспользоваться неравенством для [math]\displaystyle{ \ n }[/math] и установить, что выражение выше не превосходит суммы

[math]\displaystyle{ q_1f(x_1)+q_2f(x_2)+\ldots+(q_n+q_{n+1}) f\left( \frac {q_n}{q_n+q_{n+1}} x_n+ \frac {q_{n+1}}{q_n+q_{n+1}} x_{n+1} \right) }[/math].

Остаётся лишь применить к значению функции в последнем слагаемом неравенство для [math]\displaystyle{ \ n=2 }[/math]. Таким образом по методу математической индукции неравенство Йенсена полностью доказано.

Геометрическая интерпретация

Точка [math]\displaystyle{ (\sum \limits_{i=1}^{n} {q_i x_i};\sum \limits_{i=1}^{n} {q_i f(x_i)}) }[/math] является соответствующей выпуклой комбинацией точек [math]\displaystyle{ (x_1, f(x_1)), (x_2, f(x_2)), \dots, (x_n, f(x_n)) }[/math]. Из определения выпуклой функции очевидно, что выпуклая оболочка этого множества точек будет совпадать с самим множеством. Значит, из свойств выпуклой комбинации следует, что образованная точка будет лежать внутри многоугольника, построенного на перечисленных точках в указанном порядке (если соединить последнюю с первой).

Геометрически очевидно, что в этом случае точка [math]\displaystyle{ (\sum \limits_{i=1}^{n} {q_i x_i};\sum \limits_{i=1}^{n} {q_i f(x_i)}) }[/math] будет лежать выше одной из прямых вида [math]\displaystyle{ (x_i;f(x_i))-(x_{i+1};f(x_{i+1})) }[/math]. Но у выпуклой функции по определению такая прямая лежит выше графика функции. Значит, и точка [math]\displaystyle{ (\sum \limits_{i=1}^{n} {q_i x_i};\sum \limits_{i=1}^{n} {q_i f(x_i)}) }[/math] лежит выше этого графика, что и означает, что [math]\displaystyle{ f(\sum \limits_{i=1}^{n} {q_i x_i}) \le \sum \limits_{i=1}^{n} {q_i f(x_i)} }[/math].

Интегральная формулировка

Для выпуклой функции [math]\displaystyle{ \varphi\left( x \right) }[/math] и интегрируемой функции [math]\displaystyle{ f\left( x \right) }[/math] выполняется неравенство

[math]\displaystyle{ \varphi\left( \frac{1}{b-a} \int_a^b f(x)\, dx\right) \le \frac{1}{b-a}\int_a^b \varphi(f(x)) \,dx. }[/math]

Вероятностная формулировка

Пусть [math]\displaystyle{ (\Omega,\mathcal{F},\mathbb{P}) }[/math] — вероятностное пространство, и [math]\displaystyle{ X\colon\Omega \to \mathbb{R} }[/math] — определённая на нём случайная величина. Пусть также [math]\displaystyle{ \varphi\colon\mathbb{R} \to \mathbb{R} }[/math] — выпуклая (вниз) борелевская функция. Тогда если [math]\displaystyle{ X, \varphi(X) \in L^1(\Omega,\mathcal{F},\mathbb{P}) }[/math], то

[math]\displaystyle{ \varphi(\mathbb{E}[X]) \leqslant \mathbb{E}[\varphi(X)] }[/math],

где [math]\displaystyle{ \mathbb{E}[\cdot] }[/math] означает математическое ожидание.

Неравенство Йенсена для условного математического ожидания

Пусть в дополнение к предположениям, перечисленным выше, [math]\displaystyle{ \mathcal{G}\subset \mathcal{F} }[/math] — под-σ-алгебра событий. Тогда

[math]\displaystyle{ \varphi(\mathbb{E}[X|\mathcal{G}]) \leqslant \mathbb{E}[\varphi(X)|\mathcal{G}] }[/math],

где [math]\displaystyle{ \mathbb{E}[\cdot|\mathcal{G}] }[/math] обозначает условное математическое ожидание относительно σ-алгебры [math]\displaystyle{ \mathcal{G} }[/math].

Частные случаи

Неравенство Гёльдера

Пусть [math]\displaystyle{ \ f(x)=x^k }[/math], где [math]\displaystyle{ \ x\gt 0, }[/math] [math]\displaystyle{ \ k\gt 1 }[/math] (выпуклая функция). Имеем

[math]\displaystyle{ \left(\sum_{i=1}^{n} {q_ix_i}\right)^k \le \sum _{i=1}^{n} {q_ix_i^k} }[/math], [math]\displaystyle{ \ q_1,\ldots,q_n\gt 0 }[/math] и [math]\displaystyle{ \ q_1+\ldots+q_n=1 }[/math]

Обозначим [math]\displaystyle{ \ q_i=\frac{p_i}{p_1+\ldots+p_n} }[/math], где [math]\displaystyle{ \ p_1,\ldots,p_n }[/math]- произвольные положительные числа, тогда неравенство запишется в виде

[math]\displaystyle{ \left(\sum_{i=1}^{n} {p_ix_i}\right)^k \le \left(\sum _{i=1}^{n} {p_i}\right)^{k-1}\sum _{i=1}^{n} {p_ix_i^k} }[/math].

Заменяя здесь [math]\displaystyle{ \ p_i }[/math] на [math]\displaystyle{ \ b_i^{\frac {k}{k-1}} }[/math] и [math]\displaystyle{ \ x_i }[/math] на [math]\displaystyle{ \frac {a_i}{b_i^{\frac{1}{k-1}}} }[/math], получаем известное неравенство Гёльдера:

[math]\displaystyle{ \sum_{i=1}^{n} {a_ib_i} \le \left(\sum _{i=1}^{n} {a_i}^k\right)^\frac{1}{k}\left(\sum _{i=1}^{n} {b_i}^{\frac {k}{k-1}}\right)^\frac{k-1}{k} }[/math].

Неравенство Коши

Пусть [math]\displaystyle{ \ f(x)=\ln x }[/math] (вогнутая функция). Имеем

[math]\displaystyle{ \sum _{i=1}^{n} {q_i\ln x_i}\le \ln\left(\sum_{i=1}^{n} {q_ix_i}\right) }[/math], или [math]\displaystyle{ \ln\prod _{i=1}^{n} {x_i^{q_i}}\le \ln\sum_{i=1}^{n} {q_ix_i} }[/math], потенцируя получаем [math]\displaystyle{ \prod _{i=1}^{n} {x_i^{q_i}}\le \sum_{i=1}^{n} {q_ix_i} }[/math].

В частности при [math]\displaystyle{ q_i=\frac{1}{n} }[/math] получаем неравенство Коши (среднее геометрическое не превосходит среднего арифметического)

[math]\displaystyle{ \sqrt[n]{x_1 \ldots x_n}\le\frac{x_1+\ldots+x_n}{n} }[/math].

Неравенство между средним гармоническим и средним геометрическим

Пусть [math]\displaystyle{ \ f(x)=x\ln x }[/math] (выпуклая функция). Имеем

[math]\displaystyle{ \left( \sum_{i=1}^{n} {q_ix_i} \right) \ln \left( \sum_{i=1}^{n} {q_ix_i} \right) \le \sum_{i=1}^{n} {q_ix_i \ln x_i} }[/math]. Положив [math]\displaystyle{ q_i=\frac{\frac{1}{x_i}}{\sum_{i=1}^{n} {\frac{1}{x_i}}} }[/math] и потенцируя, получаем

[math]\displaystyle{ \frac{n}{\frac{1}{x_1} + \ldots + \frac{1}{x_n}}\le\left( x_1\cdot\ldots\cdot x_n\right)^{1/n} }[/math] (среднее гармоническое не превосходит среднего геометрического)

Неравенство между средним гармоническим и средним арифметическим

Пусть [math]\displaystyle{ \ f(x)=\frac{1}{x} }[/math] (выпуклая функция). Имеем [math]\displaystyle{ \frac{1}{\sum_{i=1}^{n} {q_ix_i}} \le \sum_{i=1}^{n} {\frac{q_i}{x_i}} }[/math]

В частности при [math]\displaystyle{ q_i=\frac{1}{n} }[/math] получаем, что среднее гармоническое не превосходит среднего арифметического:

[math]\displaystyle{ \frac{n}{\frac{1}{x_1} + \ldots + \frac{1}{x_n}}\le\frac{x_1+\ldots+x_n}{n} }[/math]

См. также

Литература

Зорич В. А. Гл. V. Дифференциальное исчисление // Математический анализ. Часть I. — 6-е изд. — М.: МЦНМО, 2012. — С. 289—290. — 2000 экз. — ISBN 978-5-94057-892-5.
Фихтенгольц Г. М. Гл. IV. Исследование функций с помощью производных // Курс дифференциального и интегрального исчисления. — 8-е изд. — М.: ФИЗМАТЛИТ, 2001. — Т. 1. — С. 336—337. — 5000 экз. — ISBN 5-9221-0156-0.