Микрополосковая линия

Циркулятор — устройство СВЧ, выполненное с использованием микрополосковой технологии

Микрополосковая линия — несимметричная полосковая линия передачи, для передачи электромагнитных волн в воздушной или, как правило, в диэлектрической среде, вдоль двух или нескольких проводников, имеющих форму тонких полосок и пластин.

Линии получили название микрополосковые, т. к. в результате высокой диэлектрической проницаемости подложки её толщина и поперечные размеры полосы много меньше длины волны в свободном пространстве.

В микрополосковой линии распространяется волна квази-ТЕМ и силовые линии электрического поля проходят не только в диэлектрике, но и вне его.

Основным достоинством микрополосковой линии и различных устройств на её основе считается возможность автоматизации производства с применением технологий изготовления печатных плат, гибридных и плёночных интегральных микросхем. Основной недостаток, ограничивающий применение, — возможность применения только при малых и средних уровнях мощности СВЧ колебаний.

Основные параметры

микрополосковая линия

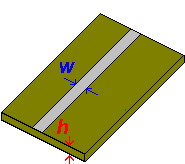
Волновое сопротивление

[math]\displaystyle{ Z_\text{Bf} }[/math] — волновое сопротивление c учётом частотной дисперсии

[math]\displaystyle{ Z_\text{Bf}=Z_\text{Bs}-\frac{Z_\text{Bs}-Z_\text{B}}{1+G(f/f_\text{p})^{2}} }[/math]

где

[math]\displaystyle{ Z_\text{Bs} }[/math] — волновое сопротивление симметричной полосковой линии шириной [math]\displaystyle{ w }[/math] и высотой [math]\displaystyle{ 2h }[/math];

[math]\displaystyle{ f_\text{p}=0,3976Z_\text{B}/h }[/math], в ГГц;

[math]\displaystyle{ h }[/math] — высота подложки; f в ГГц, а h в мм;

[math]\displaystyle{ G=\left(\frac{Z_\text{B}-5}{60}\right)^{1/2}+0{,}004Z_\text{B} }[/math]

[math]\displaystyle{ Z_\text{B} }[/math] — волновое сопротивление без учёта дисперсии;

[math]\displaystyle{ Z_\text{B} }[/math], приблизительно, с точностью до 2%, можно определить по формуле

[math]\displaystyle{ Z_\text{B} = \,\! \begin{cases} \frac{B_\text{k}}{2 \pi} \ln \left( \frac{8 h}{w_\text{eff}} + 0,25 \frac{w_\text{eff}}{h} \right), \frac{w_\text{eff}}{h} \le 1 \\ B_\text{k} \left( \frac{w_\text{eff}}{h} +1{,}393 + 0{,}667 \ln \left(\frac{w_\text{eff}}{h} + 1{,}444 \right)\right)^{-1}, \frac{w_\text{eff}}{h} \ge 1 \end{cases}, B_\text{k} = \frac{z_{0}}{\sqrt{\varepsilon_{ref(t,f)}}} }[/math]

где

[math]\displaystyle{ \varepsilon_{reff}=\varepsilon_{r}-\frac{\varepsilon_{r}-\varepsilon_{reft}} {1+G(f/f_\text{p})^{2}} }[/math] — эффективная диэлектрическая проницаемость с учётом частотной дисперсии

где

[math]\displaystyle{ f }[/math], [math]\displaystyle{ f_{p} }[/math], [math]\displaystyle{ G }[/math] см. выше

[math]\displaystyle{ \varepsilon_{reft} }[/math] — эффективная диэлектрическая проницаемость с учётом толщины проводника

[math]\displaystyle{ \varepsilon_{reft}=\,\!\begin{cases}\varepsilon_{ref}, \frac{t}{h} \le 0,005 \\ \varepsilon_{ref}-\frac{(\varepsilon_{r}-1)t/h}{4,6\sqrt{w/h}}, \frac{t}{h} \gt 0,005 \end{cases} }[/math]

[math]\displaystyle{ \varepsilon_{ref} }[/math] — эффективная диэлектрическая проницаемость.

[math]\displaystyle{ \varepsilon_{ref}=\,\! \begin{cases}\frac{\varepsilon_{r}+1}{2}+\frac{\varepsilon_{r}-1}{2}\left(1+\frac{12h}{w}\right)^{-1/2} , \frac{w}{h} \ge 1 \\ \frac{\varepsilon_{r}+1}{2}+\frac{\varepsilon_{r}-1}{2}\left(\left(1+\frac{12h}{w}\right)^{-1/2}+0,041\left( 1-\frac{w}{h}\right)^{2}\right), \frac{w}{h} \lt 1 \end{cases} }[/math]

[math]\displaystyle{ \varepsilon_{r} }[/math] — диэлектрическая проницаемость материала подложки

[math]\displaystyle{ z_{0} }[/math] — характеристическое сопротивление вакуума

[math]\displaystyle{ w_\text{eff} }[/math] — эффективная ширина проводника

[math]\displaystyle{ w_\text{eff}= \,\! \begin{cases} w, (\Delta w =0),\frac{t}{h} \le 0{,}005 \\ w + \Delta w ,\frac{t}{h} \gt 0{,}005 \end{cases}, \frac{w_\text{eff}}{h} = \frac{w}{h} + \frac{\Delta w}{h} }[/math]

[math]\displaystyle{ \frac{\Delta w}{h} = \,\! \begin{cases} A_\text{k} \left(1 + \ln \frac{4 \pi w}{t} \right), \frac{w}{h} \lt \frac{1}{2 \pi} \\ A_\text{k} \left(1 + \ln \frac{2 h}{t}\right), \frac{w}{h} \ge \frac{1}{2 \pi} \end{cases}, A_\text{k}= \frac{1,25 t}{\pi h} }[/math]

где [math]\displaystyle{ w }[/math] — ширина проводника;

[math]\displaystyle{ t }[/math] — толщина полоски;

Коэффициент затухания на единицу длины (погонное затухание)

в дБ/м

[math]\displaystyle{ \alpha = \alpha_{\partial}+\alpha_{\pi\text{p}} }[/math]

где

• [math]\displaystyle{ \alpha_{\partial} }[/math] — потери в диэлектрике

[math]\displaystyle{ \alpha_{\partial} =\frac{27,3\varepsilon_{r}}{(\varepsilon_{r}-1)} \frac{(\varepsilon_{reff}-1)}{\sqrt{\varepsilon_{reff}}}\frac{\operatorname{tg}\delta}{\lambda_{0}} }[/math],

где

[math]\displaystyle{ \operatorname{tg}\delta }[/math] — тангенс угла потерь диэлектрика;

[math]\displaystyle{ \lambda_{0} }[/math] — длина волны в свободном пространстве;

• [math]\displaystyle{ \alpha_{\pi\text{p}} }[/math] — потери в проводнике

Ссылки

• Microstrip Analysis/Synthesis Calculator