Конструкция Штейнера

1. Конструкция Штейнера

2. Перспективное отображение прямых

3. Пример конструкции Штейнера: построение точки P

Конструкция Штейнера — способ определения невырожденного конического сечения в проективной плоскости над полем. Была предложена швейцарским математиком Якобом Штейнером.

Конструкция

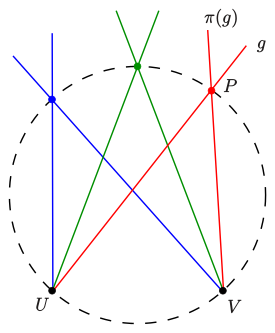
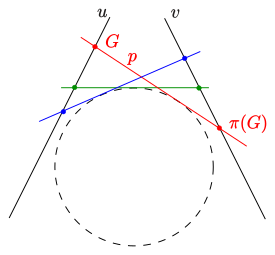
• Пусть даны два пучка прямых [math]\displaystyle{ B(U),B(V) }[/math] в точках [math]\displaystyle{ U,V }[/math] (все прямые, содержащие [math]\displaystyle{ U }[/math] и [math]\displaystyle{ V }[/math] соответственно) и проективное, но не перспективное отображение [math]\displaystyle{ \pi }[/math] из [math]\displaystyle{ B(U) }[/math] в [math]\displaystyle{ B(V) }[/math]. Тогда точки пересечения соответствующих прямых образуют невырожденное проективное коническое сечение (изображение 1)

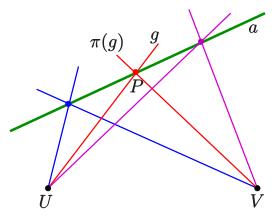
Перспективное отображение [math]\displaystyle{ \pi }[/math] пучка [math]\displaystyle{ B(U) }[/math] в пучок [math]\displaystyle{ B(V) }[/math] — это биекция, такая, что соответствующие прямые пересекаются на фиксированной прямой [math]\displaystyle{ a }[/math], называемой осью перспективного отображения [math]\displaystyle{ \pi }[/math] (изображение 2).

Проективное отображение — это композиция конечного числа перспективных отображений.

Примеры часто используемых полей — это действительные числа [math]\displaystyle{ \R }[/math], рациональные числа [math]\displaystyle{ \Q }[/math] и комплексные числа [math]\displaystyle{ \Complex }[/math]. Конструкция также работает над конечными полями, давая примеры в конечных проективных плоскостях.

Замечание: Основная теорема для проективных плоскостей утверждает, что проективное отображение в проективной плоскости над полем однозначно определяется образами трёх прямых. Это значит, что для конструкции Штейнера, кроме двух точек [math]\displaystyle{ U,V }[/math] должны быть заданы только образы трёх прямых. Поскольку образ прямой однозначно определяется точкой пересечения с образом, отсюда следует, что коника однозначно определяется пятью лежащими на ней точками.

Пример

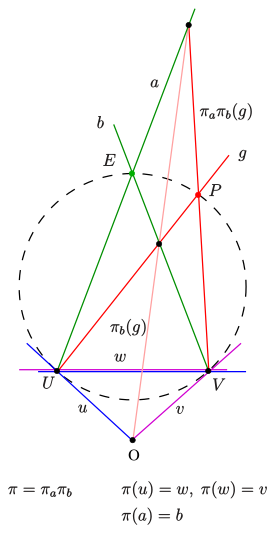
В следующем примере известны образы трёх прямых [math]\displaystyle{ a,u,w }[/math] (см. изображение 3): [math]\displaystyle{ \pi(a)=b, \pi(u)=w, \pi(w)=v }[/math]. Проективное отображение [math]\displaystyle{ \pi }[/math] является композицией перспективных отображений [math]\displaystyle{ \pi_b,\pi_a }[/math]: 1) [math]\displaystyle{ \pi_b }[/math] — это перспективное отображение пучка в точке [math]\displaystyle{ U }[/math] на пучок в точке [math]\displaystyle{ O }[/math] с осью [math]\displaystyle{ b }[/math]. 2) [math]\displaystyle{ \pi_a }[/math] — это перспективное отображение пучка в точке [math]\displaystyle{ O }[/math] на пучок в точке [math]\displaystyle{ V }[/math] с осью [math]\displaystyle{ a }[/math]. Нужно проверить, что [math]\displaystyle{ \pi=\pi_a\pi_b }[/math] обладает следующими свойствами: [math]\displaystyle{ \pi(a)=b, \pi(u)=w, \pi(w)=v }[/math]. Таким образом, для произвольной прямой [math]\displaystyle{ g }[/math] может быть построен её образ [math]\displaystyle{ \pi(g)=\pi_a\pi_b(g) }[/math]. Прямые [math]\displaystyle{ u }[/math] и [math]\displaystyle{ v }[/math] содержат только точки коники [math]\displaystyle{ U }[/math] и [math]\displaystyle{ V }[/math] соответственно. Следовательно, [math]\displaystyle{ u }[/math] и [math]\displaystyle{ v }[/math] являются касательными к построенной конике.

Доказательство того, что этот метод позволяет построить конику, производится путём перехода к аффинной карте, в которой прямая [math]\displaystyle{ w }[/math] является бесконечно удалённой прямой, точка [math]\displaystyle{ O }[/math] — началом координат, точки [math]\displaystyle{ U,V }[/math] — точками на бесконечности, соответствующими осям x и y соответственно. и точка [math]\displaystyle{ E=(1,1) }[/math]. Аффинная часть построенной коники оказывается гиперболой [math]\displaystyle{ y=1/x }[/math].

Построение Штейнера двойственной коники

Двойственный эллипс

Построенная по Штейнеру двойственная коника

Определение перспективного отображения

Пример построения двойственной коники по Штейнеру

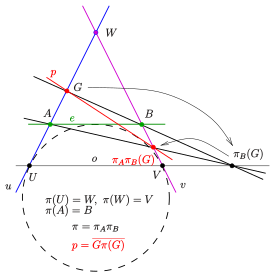
Определения

При переходе к двойственной проективной плоскости меняются местами слова «точка» и «прямая» и операции пересечения прямых и соединения точек. Двойственная проективная плоскость также является проективной плоскостью и на ней можно ввести однородные координаты. Невырожденное конической сечение в двойственной проективной плоскости также определяется квадратичной формой.

Двойственная коника может быть построена двойственным методом Штейнера:

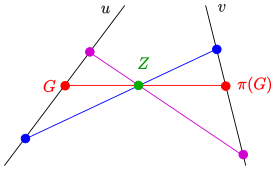
• Пусть даны прямые [math]\displaystyle{ u,v }[/math] и проективное, но не перспективное отображение [math]\displaystyle{ \pi }[/math] из [math]\displaystyle{ u }[/math] в [math]\displaystyle{ v }[/math]. Тогда прямые, соединяющие соответственные точки, образуют двойственное невырожденное проективное коническое сечение.

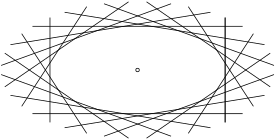
Перспективное отображение [math]\displaystyle{ \pi }[/math] множества точек на прямой [math]\displaystyle{ u }[/math] на множество точек на прямой [math]\displaystyle{ v }[/math] — это биекция, такая, что прямые, соединяющие соответственные точки, пересекаются в фиксированной точке [math]\displaystyle{ Z }[/math], которая называется центром перспективного отображения [math]\displaystyle{ \pi }[/math] (см. изображение).

Проективное отображение — это композиция конечного числа перспективных отображений.

В случае, когда основное поле имеет характеристику 2, все касательные коники пересекаются в точке, называемой узлом (или ядром) коники. Следовательно, коника, двойственная к невырожденной конике, является подмножеством двойственной прямой, а не овальной кривой (в двойственной плоскости). Так что двойственная коника является невырожденной только в том случае, когда характеристика основного поля не равна 2.

Пример

В следующем примере известны образы трёх точек [math]\displaystyle{ A,U,W }[/math]: [math]\displaystyle{ \pi(A)=B, \, \pi(U)=W,\, \pi(W)=V }[/math]. Проективное отображение [math]\displaystyle{ \pi }[/math] может быть представлено как композиция перспективных отображений [math]\displaystyle{ \pi_B,\pi_A }[/math]:

1) [math]\displaystyle{ \pi_B }[/math] — это перспективное отображение множества точек на прямой [math]\displaystyle{ u }[/math] на множество точек на прямой [math]\displaystyle{ o }[/math] с центром [math]\displaystyle{ B }[/math].

2) [math]\displaystyle{ \pi_A }[/math] — это перспективное отображение множества точек на прямой [math]\displaystyle{ o }[/math] на множество точек на прямой [math]\displaystyle{ v }[/math] с центром [math]\displaystyle{ A }[/math].

Лекгко проверяется, что отображение [math]\displaystyle{ \pi=\pi_A\pi_B }[/math] удовлетворяет [math]\displaystyle{ \pi(A)=B,\, \pi(U)=W, \, \pi(W)=V }[/math]. Таким образом, для произвольной точки [math]\displaystyle{ G }[/math] может быть построен её образ [math]\displaystyle{ \pi(G)=\pi_A\pi_B(G) }[/math] и прямая [math]\displaystyle{ \overline{G\pi(G)} }[/math] является элементом двойственной коники.

Литература

• Coxeter, H. S. M. The Real Projective Plane, Springer Science & Business Media, 1993
• Hartmann, Erich, Planar Circle Geometries, an Introduction to Moebius-, Laguerre- and Minkowski Planes
• Merserve, Bruce E. Fundamental Concepts of Geometry, Dover, (1983) [1959], ISBN 0-486-63415-9