Изоклина

Синим цветом изображены изоклины уравнения [math]\displaystyle{ y'=y }[/math]

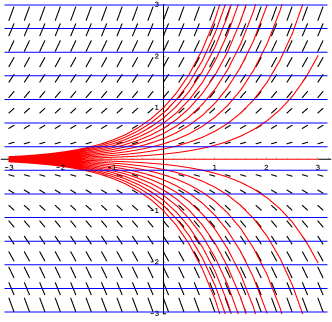
Изокли́на (от др.-греч. ίσος «равный, одинаковый, подобный» + κλίνω «клонить, наклонять») дифференциального уравнения первого порядка — кривая на плоскости, вдоль которой поле, задаваемое дифференциальным уравнением, имеет один и тот же наклон.

Описание

Изоклина дифференциального уравнения [math]\displaystyle{ y'=f(x,\;y) }[/math], отвечающая наклону [math]\displaystyle{ p }[/math], есть линия уровня правой части соответствующего дифференциального уравнения:

[math]\displaystyle{ f(x,\;y)=p. }[/math]

Задавая различные значения параметра [math]\displaystyle{ p }[/math], можно получить семейство кривых, каждая из которых является изоклиной при определённом значении параметра [math]\displaystyle{ p }[/math]. Построение изоклин — один из приёмов качественного анализа поведения решений анализируемого дифференциального уравнения.

Литература

• Филиппов А. Ф. Введение в теорию дифференциальных уравнений. — 2-е изд. — М.: КомКнига, 2007. — 240 с. — (Классический учебник МГУ). — ISBN 978-5-484-00786-8..