Зонд Ленгмюра

Зонд Ленгмюра — устройство, используемое для диагностики плазмы. Зондовый метод был впервые предложен Ирвингом Ленгмюром в 1923 году. Этот метод основан на измерении плотности тока заряженных частиц на помещённый в плазму электрический проводник в зависимости от его потенциала. Соответствующая кривая называется зондовой вольт-амперной характеристикой. Наибольшее распространение при исследованиях получили цилиндрический, сферический и плоский зонды.

Устройство

Проводящая часть зонда, находящаяся в плазме, может быть выполнена из любого металла. Выбор металла определяется прежде всего свойствами среды, в которую он помещён, и характеристиками изолятора, с которым он имеет механический контакт. Этим металлом может быть, например, молибден, вольфрам, а в случае химически агрессивной среды — золото, платина. Изолирующая часть зонда изготавливается из стекла, кварца или различных типов керамики. Типичным для цилиндрического зонда является диаметр от 10⁻³ до 10⁻¹ см, для сферического 10⁻²-10⁻¹ см, при этом длина той части цилиндрического зонда, которая непосредственно собирает заряженные частицы, составляет 10⁻¹-10⁰ см (указанные размеры зависят от параметров плазмы).

Особенность метода

Зондовый метод является контактным методом диагностики. С этим обстоятельством связано одно из его преимуществ по сравнению, например с СВЧ-методами исследования плазмы, а именно локальность определения параметров плазмы. В то же время контактный характер измерений приводит к возмущению плазмы в некоторой области около зонда. Характерные размеры такой области определяются дебаевским радиусом экранирования и, как правило, оказываются существенно меньше размеров плазменного объёма. Так, при концентрации заряженных частиц 10¹² см⁻³ и температуре электронов 1 эВ дебаевский радиус имеет порядок 10⁻³ см, что, как видно, позволяет проводить зондовые измерения и в плазме малых линейных размеров.

Схема измерительной системы

Измерительная система включает в себя измерительный зонд, опорный электрод – противозонд (в качестве него может выступать анод А или катод К, обычно в качестве опорного используют анод, так как в этом случае требуется источник зондового смещения Б2 на меньшее предельное напряжение) и источник напряжения (Рис. 2). Питание разряда осуществляется источником Б1. Зонду придают различные значения потенциала, относительно опорного электрода. Погруженный в плазму, зонд окружается двойным электрическим слоем (призондовый слой) и, фактически, ВАХ зонда является ВАХ слоя. В случае, когда размеры измерительного зонда много меньше размеров опорного электрода, ВАХ системы определяется слоем у измерительного зонда (система одиночного зонда).

Вольт-амперная характеристика зонда Ленгмюра

**Рис. 3** Зондовая вольт-амперная характеристика

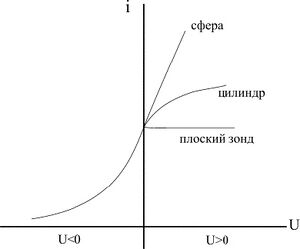
[math]\displaystyle{ U }[/math] — разность потенциалов между измерительным (З) и опорным (А) зондами

[math]\displaystyle{ U_{sp} }[/math] — потенциал плазмы

[math]\displaystyle{ U_{fl} }[/math] — плавающий потенциал

[math]\displaystyle{ U_{3} = U-U_{sp} }[/math] — потенциал измерительного зонда относительно плазмы.

Участки зондовой характеристики (Рис. 3):

I — [math]\displaystyle{ U_{3} \gt 0 }[/math] — электронный ток насыщения

II — [math]\displaystyle{ U_{3} \le 0 }[/math] — электронный ток на зонд

III — [math]\displaystyle{ U_{3} \lt 0, U_{3} \gg kT_{e}/e }[/math] — ионный ток насыщения,

где [math]\displaystyle{ T_e }[/math] — температура электронов, [math]\displaystyle{ k }[/math] — постоянная Больцмана, [math]\displaystyle{ e }[/math] — заряд электрона

В случае максвелловского распределения электронов по энергиям в невозмущённой плазме и больцмановского распределения концентрации заряженных частиц в поле слоя пространственного заряда [math]\displaystyle{ n=n_{0} e^{-eU/kT_{e}} }[/math] у зонда ток зонда любой формы при отрицательных потенциалах [math]\displaystyle{ U_{3} }[/math] определяется соотношением:

[math]\displaystyle{ i_{3} (U_{3})= \frac{1}{4} en_{e} \bar{v}_{e} S_{3} e^{((eU_{3})/(kT_{e}))}, U_{3}\lt 0 }[/math]

где [math]\displaystyle{ \bar{v}=\sqrt{8kT_{e}/\pi m} }[/math] — средняя скорость электронов, [math]\displaystyle{ n_{e} }[/math] — концентрация электронов, [math]\displaystyle{ S_{3} }[/math] — площадь зонда, [math]\displaystyle{ T_{e} }[/math]— температура электронов.

Это соотношение было получено Ирвингом Ленгмюром и Харольдом Мотт-Смитом в 1926 году и явилось основой зондового метода диагностики плазмы. При [math]\displaystyle{ U_{3} \gt 0 }[/math] ВАХ зависит от формы зонда. Но, несмотря на кажущуюся простоту, зондовый метод является довольно нетривиальным. Это в первую очередь связано с тем что плазма и зонд должны удовлетворять ряду достаточно жестких требований и только тогда результаты простых электрических измерений могут быть связаны с параметрами плазмы.

Критерии для работы с зондом Ленгмюра

Основные предположения простейшей теории, при выполнении которой можно довольно быстро провести расчёт зондовой характеристики, представленные в работах Ленгмюра и Бома, приведены ниже:

Характерный размер области однородной плазмы много больше длины свободного пробега электрона и иона. Плазма изотропна;
Средние длины энергетического пробега электронов [math]\displaystyle{ \lambda_{i} }[/math] велики по сравнению с радиусом зонда [math]\displaystyle{ r_{3} }[/math] и толщиной призондового слоя [math]\displaystyle{ h }[/math];
Отсутствуют генерация и рекомбинация заряженных частиц в слое около зонда;
В плазме отсутствует магнитное поле;
Держатель зонда не влияет на характеристики плазмы и следовательно на измерения;
Отсутствует отражение электронов от зонда и их вторичная эмиссия, не образуется плёнки на поверхности зонда в результате химических реакций (что может повлиять на отражение и вторичную эмиссию электронов с поверхности);
Отсутствуют колебания потенциала плазмы (относительно потенциала опорного электрода);
Работа выхода электронов с поверхности зонда одинакова в различных точках;
Потенциал плазмы постоянен на характерных размерах зонда.

Режимы работы

В зависимости от соотношения характерных размеров зонда [math]\displaystyle{ r_{3} }[/math] и характерных масштабов плазмы (длины свободного пробега электронов [math]\displaystyle{ \lambda_{e} }[/math] и ионов [math]\displaystyle{ \lambda_{i} }[/math], длины релаксации энергии электронов [math]\displaystyle{ \lambda_{\varepsilon e} }[/math] и ионов [math]\displaystyle{ \lambda_{\varepsilon i} }[/math], дебаевского радиуса экранирования [math]\displaystyle{ \lambda_{d} }[/math], толщина слоя пространственного заряда у зонда [math]\displaystyle{ h }[/math] ) различают несколько режимов работы зонда.

При этом нужно учитывать, что:

[math]\displaystyle{ \lambda_{e} \ll \lambda_{\varepsilon e}=\lambda_{\varepsilon}=\delta^{-1/2} \lambda_{e} }[/math]
где [math]\displaystyle{ \delta = 10^{-4} -10^{-2} }[/math] – средняя доля потери энергии электроном в одном столкновении, в то время как для ионов [math]\displaystyle{ \delta \approx 1, \lambda_{i} \approx \lambda_{\varepsilon i} }[/math]

При [math]\displaystyle{ \lambda_{e}, \lambda_{i} \gg r_{3}+h }[/math] реализуются условия бесстолкновительного слоя (классический зонд Ленгмюра).
При [math]\displaystyle{ \lambda_{e} \ll r_{3}+h \ll \lambda_{\varepsilon} }[/math] реализуется диффузионный режим для электронов.
При [math]\displaystyle{ r_{3}+h \gg \lambda_{\varepsilon},\lambda_{i} }[/math] реализуется режим сплошной среды.

В первых двух случаях из результатов зондовых измерений можно получить информацию о ФРЭЭ (ФРЭЭ - функция распределения электронов по энергиям, которая в случае Максвелловского распределения характеризуется температурой электронов — T_e) в невозмущённой плазме (хотя соотношения для этого оказываются разными). В третьем случае возможно лишь получение информации о температуре электронов. Таким образом, для корректного анализа результатов зондовых измерений и использования соответствующих теоретических представлений необходимо определить в каком режиме будет работать зонд. Теория, предложенная Ленгмюром предполагает, что [math]\displaystyle{ \lambda_{d} \ll \lambda_{min} }[/math], где [math]\displaystyle{ \lambda_{min} }[/math] – минимальная длина энергетического пробега электронов. Тем самым определяется нижняя граница концентрации электронов в плазме:

[math]\displaystyle{ n_{e}\gg 5 \cdot 10^{5} T_{e} (N\langle\sigma(\varepsilon)\rangle)^{2} }[/math]

где [math]\displaystyle{ T_{e} }[/math] — температура электронов в эВ, [math]\displaystyle{ n_{e} }[/math] – концентрация электронов в см⁻³, [math]\displaystyle{ N }[/math] – концентрация тяжелых частиц в см⁻³, [math]\displaystyle{ \langle\sigma(\varepsilon)\rangle }[/math] – среднее значение сечения столкновений электронов с тяжелыми частицами в см².

Методика измерений

Методика измерений Для использования зондовых характеристик при расчёте параметров плазмы необходимо знать потенциал измерительного зонда относительно потенциала плазмы [math]\displaystyle{ U_{sp} }[/math] (потенциал пространства). Но из экспериментов нам известен лишь потенциал относительно некоторого опорного электрода [math]\displaystyle{ U }[/math] и [math]\displaystyle{ U_{3} = U - U_{sp} }[/math]. В соответствии с классическими представлении [math]\displaystyle{ U_{sp} }[/math] определяется как потенциал точки перегиба ВАХ зонда. В реальных ВАХ из-за влияния ряда факторов (загрязнение поверхности зонда, сток электронов на зонд, колебания потенциала плазмы) явно выраженный перегиб отсутствует. Для определения [math]\displaystyle{ U_{sp} }[/math] используются характерные точки на производных зондового тока по потенциалу зонда. Существует два подхода к определению: [math]\displaystyle{ U_{sp} }[/math] соответствует потенциалу зонда, при котором [math]\displaystyle{ \frac{d^{2} i_{3}}{dU_{3}^{2}} }[/math] либо максимальна, либо равна 0.

Хотя величиной, представляющей интерес для диагностики плазмы, является потенциал плазмы [math]\displaystyle{ U_{sp} }[/math], легче измерять плавающий потенциал [math]\displaystyle{ U_{fl} }[/math]. Плавающий потенциал – это потенциал зонда относительно плазмы, при котором ток на зонд равен нулю. Ясно, что [math]\displaystyle{ U_{fl} }[/math] всегда отрицателен. Величина [math]\displaystyle{ U_{fl} }[/math] может быть определена при известных зависимостях ионного тока насыщения и электронного тока от потенциала зонда. Так, в предположении максвелловского распределения электронов по энергиям получается следующее выражение для плавающего потенциала:

[math]\displaystyle{ \frac{eU_{fl}}{kT_{e}}\approx-\ln\left [\frac{e}{\sqrt{4\pi}}\sqrt{\frac{M}{m}} \right ] \approx-\ln \left [ 0{,}77\sqrt{M/m} \right ] }[/math], где M – масса основного иона

Для водорода плавающий потенциал:
[math]\displaystyle{ U_{fl} }[/math] [B] [math]\displaystyle{ \approx-3{,}3 kT_{e} }[/math] [эВ]

Для аргона:
[math]\displaystyle{ U_{fl} }[/math] [B] [math]\displaystyle{ \approx-6{,}3 kT_{e} }[/math] [эВ]

Если функция распределения электронов в разных точках плазмы одинакова, то распределение [math]\displaystyle{ U_{flo} }[/math] определяет распределение потенциала плазмы. При произвольной форме изотропного энергетического распределения электронов (ФРЭЭ) в области отрицательных потенциалов зонда электронный ток на зонд связан с [math]\displaystyle{ f(\varepsilon) }[/math] интегральным соотношением:
[math]\displaystyle{ i_{e}(U_{e})=\frac{2\pi n_{e} eS_{3}}{m^2}\int\limits_{eU_{3}}^{\infty} f(\varepsilon)(\varepsilon-eU_{3} )d\varepsilon }[/math], где [math]\displaystyle{ \varepsilon }[/math] – энергия электрона, [math]\displaystyle{ f(\varepsilon) }[/math] – ФРЭЭ [math]\displaystyle{ (f(\varepsilon)=n_{e} f_{o} (\varepsilon), \int\limits_{0}^{\infty} f(\varepsilon) \sqrt{\varepsilon} d\varepsilon=1) }[/math]

Данное выражение справедливо для зондов с выпуклой поверхностью, при отсутствии отражения электронов от зонда и вторичной электронной эмиссии с зонда, отсутствии генерации и рекомбинации носителей зарядов в слое, одинаковой работе выхода электронов с поверхности зонда в различных точках, отсутствии загрязнения поверхности зонда, отсутствии магнитного поля и колебаний потенциала плазмы. При этом также необходимо, чтобы не только зонд, но и его держатель не возмущали плазму. Существенным шагом в развитии зондовой диагностики плазмы было решение Дрювестейном задачи о нахождении ФРЭЭ по второй производной электронного тока на зонд [math]\displaystyle{ i_{e}(U_{3}) }[/math] по потенциалу зонда [math]\displaystyle{ U_{3}\lt 0 }[/math]

[math]\displaystyle{ n_{e}f_{o}(\varepsilon)=2^{3/2} \frac{\sqrt{mU_{3}}}{S_{3} e^{3/2}} \frac{d^{2} i_{e} (U_{3})} {dU_{3}^{2}} }[/math]

где [math]\displaystyle{ S_{3} }[/math] – площадь поверхности зонда. Это выражение справедливо для изотропных ФРЭЭ и не зависит от геометрии зонда, если его поверхность выпуклая. В предположении максвелловской ФРЭЭ по ВАХ может быть определена температура электронов [math]\displaystyle{ T_{e} }[/math]:

[math]\displaystyle{ kT_{e}/e=- \left ( \frac{d(\ln i_{e} )}{(dU_{3} )}\right ) ^{-1} }[/math]

Концентрация электронов может быть определена по хаотическому току на зонд при потенциале плазмы [math]\displaystyle{ U_{sp} }[/math] (электронный ток насыщения):

[math]\displaystyle{ n_{e}=4i_{e}(U_{sp})/(e\bar{v}S_{3}) }[/math]

Концентрация ионов [math]\displaystyle{ n_{i} }[/math] определяется по ВАХ в области ионного тока насыщения. Это одна из наиболее сложных задач зондовой диагностики: необходимо использовать выражение для ионного тока, соответствующего условиям экспериментов (геометрии и размером зонда и соотношению последних λ и λ_D), а также знать ионный состав плазмы.

Для оценок часто используется соотношение:

[math]\displaystyle{ i_{i}=en_{i} S_{3} \sqrt{\frac{kT_{e}}{2\pi M}} \left ( \frac{eU_{3}}{kT_{e}} \right ) ^{n} }[/math]

где n определяется экспериментальным путём. Для тонкого зонда и бесстолкновительного слоя (r₃ << λ, λ_D), n = 0,5

Влияние стока электронов на зонд

Так как диффузия электронов из невозмущённой плазмы не успевает компенсировать их потери, связанные с уходом их на зонд, то свойства плазмы в окрестности зонда могут изменятся. Возмущение плазмы вызывает, соответственно, искажение ВАХ зонда тем большее, чем ближе потенциал зонда к потенциалу плазмы и чем больше параметр стока [math]\displaystyle{ \delta }[/math]. Параметр стока зависит от геометрии зонда и соотношения характерных размеров зонда и длины свободного пробега электронов. Так например для цилиндрического зонда:

[math]\displaystyle{ \delta_{cyl} = \frac{3r_{3}}{4\lambda} \ln (l_{3}/2r_{3} ) }[/math], где [math]\displaystyle{ l_{3} }[/math] – длина зонда

Сток электронов приводит к занижению рассчитанной по электронному току ФРЭЭ, и к завышению определённой по ВАХ температуре электронов, к искажению второй производной зондового тока по потенциалу зонда. Влияние стока может быть скорректировано расчетным путём. При [math]\displaystyle{ \delta \ll 1 }[/math] истинные и искажённые концентрации связаны следующим соотношением:

[math]\displaystyle{ n_{eo}\approx (1+4\delta/3) n_{e~dist} }[/math]

для средней энергии электронов:
[math]\displaystyle{ \bar{\varepsilon}_{o}=\bar{\varepsilon}_{dist} (1-\delta/2) }[/math]

При [math]\displaystyle{ \delta \gg 1 }[/math] из зондовой характеристики может быть получена ФРЭЭ, однако она оказывается пропорциональной не второй, а первой производной электронного тока на зонд по потенциалу зонда.

ВЧ-компенсированный зонд

При зондовых измерениях в плазме, создаваемой переменными полями (ВЧ и СВЧ разряды), а также в плазме в присутствии колебаний потенциала плазмы возможно искажение ВАХ зонда. Это связано с тем, что слой пространственного заряда у зонда является нелинейным элементом и при воздействии на него переменного напряжения происходит преобразование частоты и, в частности, в переменном сигнале появляется постоянная составляющая (выпрямление на слое, как нелинейном элементе). Это ведёт к появлению дополнительного (к внешнему напряжению) смещения зонда, причем величина этого смещения зависит от потенциала зонда.

При приложении к призондовому слою напряжения в виде: [math]\displaystyle{ U_{3} = U_{3o} + u_{o}\cos\omega t }[/math]
в предположении максвелловского распределения электронов по энергиям величина среднего электронного тока на зонд (искажённая ВАХ в области отталкивающих потенциалов) записывается в виде:
[math]\displaystyle{ i_{e}^{*}=i_{es} \exp \left ( -\frac{eU_{3o}}{kT_{e}} \right )I_{o}\left ( \frac {eu_{o}(U_{3o})}{kT_{e}} \right ) }[/math] где [math]\displaystyle{ i_{es} }[/math] – электронный ток насыщения, [math]\displaystyle{ I_{o}\left ( \frac {eu_{o}(U_{3o})}{kT_{e}} \right ) }[/math] – модифицированная функция Бесселя нулевого порядка, [math]\displaystyle{ U_{3o} }[/math] и [math]\displaystyle{ u_{o} }[/math] постоянное напряжение и амплитуда переменного напряжения на призондовом слое. Из этого выражения видно, что одинаковые значения электронного тока на зонд на искажённой характеристике ([math]\displaystyle{ u_{o} \ne 0 }[/math]) достигаются при больших отрицательных значениях внешнего смещения, чем на неискажённой характеристике ([math]\displaystyle{ u_{o} = 0 }[/math])
(Рис. 5)

Одним из следствий влияния переменного напряжения на ВАХ является смещение плавающего потенциала зонда в область больших отрицательных потенциалов при увеличении [math]\displaystyle{ eu_{o}/kT_{e} }[/math]

[math]\displaystyle{ \Delta U_{fl}=-\left ( \frac{kT_e}{e} \right ) \ln I_{o} \left ( \frac{eu_{0}}{kT_e} \right ) }[/math]

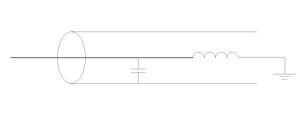
Это соотношение даёт критерий влияния [math]\displaystyle{ u_{o} }[/math] на ВАХ. Для получения наиболее точных результатов при проведении эксперимента необходимо добиться минимального значения [math]\displaystyle{ \Delta U_{fl} }[/math]. Все методы уменьшения этой погрешности (пассивные и активные) связаны с уменьшением переменного напряжения на призондовом слое. Напряжение на призондовом слое будет складываться из суммы напряжения поданного на зонд и переменного напряжения в призондовом слое: [math]\displaystyle{ u_{3}= u_{3o}+\tilde{u_{sp}} }[/math]. Добавка переменного напряжения будет определяется следующим образом [math]\displaystyle{ \tilde{u_{3}}=\tilde{u_{sp}} \frac {z_{1}} {z_{1}+z_{2}} }[/math]. Очевидно что минимальное значение [math]\displaystyle{ \tilde{u_{3}} }[/math] достигается при [math]\displaystyle{ z_{1} \rightarrow 0 }[/math] и [math]\displaystyle{ z_{2}\rightarrow \infty }[/math] (Рис. 6 (а)). Для этих целей можно использовать каскад резонансных фильтров пробок (Рис. 6 (б)). Фильтрующие элементы должны быть расположены максимально близко к активной области зонда для исключения влияние паразитных ёмкостей. Иначе эти ёмкости могут свести к нулю все усилия по уменьшению влияния [math]\displaystyle{ \tilde{u_{3}} }[/math].

Развитие зондового метода

Развитие зондовых методов происходило по двум основным направлениям:

1. Отказ от упрощённых предположений, изложенных выше и создание зондовых теорий для более сложных случаев.

Допускается произвольное соотношение между длинами пробега заряженных частиц, радиусом зонда и размером слоя объёмного заряда;
В призондовом слое объёмного заряда происходят плазмохимические процессы;
Ненулевые коэффициенты: отражения от зонда, вторичной эмиссии электронов с поверхности зонда;
Плазма анизотропна, имеются направленные потоки частиц;
Плазма нестационарна и находится в магнитном поле.

2. Усовершенствование зондовых измерительных схем

Системы с временным разрешением
Создание схем для измерения в условиях плазменных шумов
Повышение чувствительности схем
Автоматизация зондовых измерений

В настоящее время зонды используются для изучения разрядов постоянного тока, ВЧ и СВЧ разрядов при давлениях от миллиторр до атмосферного, плазмы в магнитных полях и плазмы с химическими реакциями.

Фотографии вч-компенсированного зонда

Зонд в плазме

Ссылки

[1] Ю. А Лебедев. Электрические зонды в плазме пониженного давления. 2002.
Райзер Ю. П. Физика газового разряда. 3-е изд. переработанное и дополненное. – Долгопрудный: Издательский дом “Интеллект”, 2009.
Демидов В. И., Колоколов Н. Б., Кудрявцев А. А. Зондовые методы исследования низкотемпературной плазмы. Энергоатомиздат, 1996.
Mott-Smith H., Langmuir I. // Phys. Rev. 1926. V. 28. № 5. P. 727.
Godyak V. A. Measuring EEDF in gas discharge plasmas. GTE Products Corporation. 1990.
Godyak V. A. and Demidov V. I. // Journal of Physics D: Applied Physics 2011. V. 44. P. 233001.
Demidov V.I., Ratynskaia S.V., and Rypdal K. // Review of Scientific Instruments 2002. V. 73, № 10. P. 3409.