Горизонт


Горизо́нт (др.-греч. ὁρίζων — буквально: ограничивающий) — граница неба с земной или водной поверхностью[1]. По другому определению в понятие включают также видимую часть этой поверхности[2]. Различают горизонт видимый и горизонт истинный. Угол между плоскостью истинного горизонта и направлением на видимый горизонт называют наклонением горизонта (синонимы: понижение горизонта, депрессия горизонта)[3]. На иллюстрации: точка A — точка наблюдения; Н'Н — плоскость истинного горизонта; отрезок AC1 — геометрическая (теоретическая) дальность видимого горизонта; дуга AB1 — географическая дальность видимого горизонта; угол α — наклонение горизонта; B1B2B3B4 — линия видимого горизонта.
Видимый горизонт

Видимым горизонтом называют и линию, по которой небо кажется граничащим с поверхностью Земли, и пространство неба над этой границей, и видимую наблюдателем поверхность Земли, и всё видимое вокруг наблюдателя пространство, до конечных пределов его[4]. Таким же образом понятие горизонта может быть определено для других небесных тел[5].
Синонимы: небосклон, кругозор, небозём, небоскат, закат неба, глазоём, зреймо, завесь, закрой, озор, овидь, окоём, оглядь[6].
Расстояние до видимого горизонта


- В случае, если видимый горизонт определять как границу между небом и Землёй, то рассчитать геометрическую дальность видимого горизонта можно, воспользовавшись теоремой Пифагора:
- [math]\displaystyle{ d=\sqrt{(R+h)^2-R^2} }[/math]
- Здесь d — геометрическая дальность видимого горизонта, R — радиус Земли, h — высота точки наблюдения относительно поверхности Земли[7].
- В приближении, что Земля — идеально круглая и без учёта рефракции эта формула даёт хорошие результаты вплоть до высот расположения точки наблюдения порядка 100 км над поверхностью Земли.
- Принимая радиус Земли равным 6371 км и отбрасывая из-под корня величину h2, которая не слишком значима ввиду малого отношения h/R, получим ещё более простую приближённую формулу[8]:
- [math]\displaystyle{ d \approx 113\sqrt{h} \,, }[/math]
где d и h в километрах или
[math]\displaystyle{ d \approx 3,57\sqrt{h} \,, }[/math]
где d в километрах, а h в метрах. - Ниже приведено расстояние до горизонта при наблюдении с различных высот[9]:
| Высота над поверхностью Земли h | Расстояние до горизонта d | Пример места наблюдения |
|---|---|---|
| 1,75 м | 4,7 км | стоя на земле |
| 25 м | 17,9 км | 8-этажный дом |
| 50 м | 25,3 км | колесо обозрения |
| 150 м | 43,8 км | воздушный шар |
| 2 км | 159,8 км | гора |
| 10 км | 357,3 км | самолёт |
| 350 км | 2114,0 км | МКС |

Геометрическое расстояние до горизонта [math]\displaystyle{ d }[/math] в зависимости от высоты над поверхностью [math]\displaystyle{ h }[/math] точки наблюдения.
График построен по формуле: [math]\displaystyle{ d=\sqrt{(R+h)^2-R^2}, }[/math] [math]\displaystyle{ R }[/math] – радиус Земли, принят равным 6371 км.- Для облегчения расчётов дальности горизонта в зависимости от высоты точки наблюдения и с учётом рефракции составлены таблицы и номограммы. Действительные значения дальности видимого горизонта могут значительно отличаться от табличных, особенно в высоких широтах, в зависимости от состояния атмосферы и подстилающей поверхности[10][11].
- Поднятие (снижение) горизонта относится к явлениям, связанным с рефракцией (рисунок 2). При положительной рефракции видимый горизонт поднимается (расширяется), географическая дальность видимого горизонта увеличивается по сравнению с геометрической дальностью, видны предметы, обычно скрытые кривизной Земли.
- Большие градиенты температуры создаются при сильном нагреве земной поверхности солнечными лучами, часто в пустынях, в степях. Большие градиенты могут возникнуть и в средних, и даже в высоких широтах в летние дни при солнечной погоде: над песчаными пляжами, над асфальтом, над обнажённой почвой. Такие условия являются благоприятными для возникновения нижних миражей[12].
- При отрицательной рефракции видимый горизонт снижается (сужается), не видны даже те предметы, которые видны в обычных условиях.
- В случае, если видимый горизонт определять как всё видимое вокруг наблюдателя пространство, до конечных пределов его, то расстояние до видимого горизонта, например, в лесу — это максимальное расстояние на которое уходит взгляд, пока не упрётся в деревья (несколько десятков метров), а для наблюдаемой Вселенной расстояние до видимого горизонта (то есть до самых далёких звёзд, которые мы можем наблюдать) составит около 13—14 млрд световых лет[13].
- Кстати: Космический горизонт (горизонт частиц) — это и мысленно воображаемая сфера с радиусом, равным расстоянию, которое свет прошёл за время существования Вселенной, и все множество точек Вселенной, находящихся на этом расстоянии[14].
Дальность видимости

Щёлкните по изображению, чтобы увеличить его.
На рисунке справа дальность видимости объекта определяют по формуле
[math]\displaystyle{ D_\mathrm{BL} = 3.57\,(\sqrt{h_\mathrm{B}} + \sqrt{h_\mathrm{L}}) }[/math],
где [math]\displaystyle{ D_\mathrm{BL} }[/math] — дальность видимости в километрах,
[math]\displaystyle{ h_\mathrm{B} }[/math] и [math]\displaystyle{ h_\mathrm{L} }[/math] — высоты точки наблюдения и объекта в метрах.
Если учесть земную рефракцию, то формула примет вид:
[math]\displaystyle{ D_\mathrm{BL} \lt 3.86\,(\sqrt{h_\mathrm{B}} + \sqrt{h_\mathrm{L}}) \,. }[/math]
То же самое, но [math]\displaystyle{ D_\mathrm{BL} }[/math] — в морских милях:
[math]\displaystyle{ D_\mathrm{BL} \lt 2.08\,(\sqrt{h_\mathrm{B}} + \sqrt{h_\mathrm{L}}) \,. }[/math]
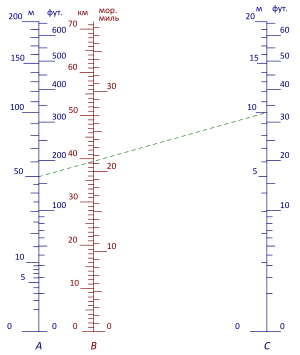
Для приближённого расчёта дальности видимости объектов применяют номограмму Струйского (см. илл.): на двух крайних шкалах номограммы отмечают точки, соответствующие высоте точки наблюдения и высоте объекта, затем проводят через них прямую и на пересечении этой прямой со средней шкалой получают дальность видимости объекта[15].
На морских картах, в лоциях и других навигационных пособиях дальность видимости маяков и огней указывается для высоты точки наблюдения равной 5 м[10]. Если высота точки наблюдения иная, то вводится поправка[16].
Горизонт на Луне

Нужно сказать, что расстояния на Луне очень обманчивы. Благодаря отсутствию воздуха удалённые предметы видятся на Луне более чётко и поэтому всегда кажутся ближе.
— Николай Носов. «Незнайка на Луне». 1964.
Лунный горизонт практически вдвое ближе земного. При этом расстояние до лунного горизонта зрительно определить крайне сложно по причине отсутствия атмосферы[17], а также объектов известного размера, по которым можно бы судить о масштабе.
Истинный горизонт
Истинный горизонт — мысленно воображаемый большой круг небесной сферы, плоскость которого перпендикулярна отвесной линии в точке наблюдения. Аналогично общему понятию, истинным горизонтом может называться не круг, а окружность, то есть линия пересечения небесной сферы и плоскости, перпендикулярной отвесной линии.
Синонимы: математический горизонт, астрономический горизонт[18].
Искусственный горизонт — прибор, которым пользуются для определения истинного горизонта.
Например, истинный горизонт легко определить, если поднести к глазам стакан с водой так, чтобы уровень воды был виден как прямая линия[19].
Горизонт в философии
Понятие горизонта в философию вводит Эдмунд Гуссерль, а Гадамер определяет его следующим образом: «Горизонт — поле зрения, охватывающее и обнимающее все то, что может быть увидено из какого-либо пункта»[20]
См. также
Примечания
- ↑ Значения слова «горизонт» на сайте gramota.ru.
- ↑ Статья «Горизонт» в Большой советской энциклопедии
- ↑ Ермолаев Г. Г., Андронов Л. П., Зотеев Е. С., Кирин Ю. П., Черниев Л. Ф. Морское судовождение / под общей редакцией капитана дальнего плавания Г. Г. Ермолаева. — издание 3-е, переработанное. — М.: Транспорт, 1970. — 568 с.
- ↑ [dic.academic.ru/searchall.php?SWord=%D0%B2%D0%B8%D0%B4%D0%B8%D0%BC%D1%8B%D0%B9+%D0%B3%D0%BE%D1%80%D0%B8%D0%B7%D0%BE%D0%BD%D1%82&stype=0 Словари и энциклопедии на Академике]. Толкования выражения «видимый горизонт». Архивировано 3 февраля 2012 года.
- ↑ Изучение Солнечной системы (недоступная ссылка). Горизонт. Космос и астрономия. Архивировано 4 марта 2016 года.
- ↑ Даль В. И. Толковый словарь живого великорусского языка. — М.: ОЛМА Медиа Групп, 2011. — 576 с. — ISBN 978-5-373-03764-8.
- ↑ Верюжский Н. А. Мореходная астрономия: Теоретический курс. — М.: РКонсульт, 2006. — 164 с. — ISBN 5-94976-802-7.
- ↑ Перельман Я. И. Горизонт // Занимательная геометрия. — М.: Римис, 2010. — 320 с. — ISBN 978-5-9650-0059-3.
- ↑ Вычислено по формуле «расстояние = 113 корней из высоты», таким образом, влияние атмосферы на распространение света не учитывается и предполагается, что Земля имеет форму шара.
- ↑ 10,0 10,1 Мореходные таблицы (МТ-2000). Адм. № 9011 / главный редактор К. А. Емец. — СПб.: ГУН и О, 2002. — 576 с.
- ↑ Мир путешествий и приключений. Расчёт расстояния до горизонта и прямой видимости онлайн.
- ↑ Всё о космосе (недоступная ссылка). Какой горизонт дальше?. Архивировано 3 февраля 2012 года.
- ↑ Лукаш В. Н., Михеева Е. В. Физическая космология. — М.: Физико-математическая литература, 2010. — 404 с. — ISBN 5922111614.
- ↑ Климушкин Д. Ю.; Граблевский С. В. Космология (недоступная ссылка). Космический горизонт (2001). Архивировано 24 марта 2012 года.
- ↑ starpomlom Учебник судоводителя любителя. Глава VII . Навигация.
- ↑ Яхтенная энциклопедия (недоступная ссылка). Видимый горизонт и дальность видимости. Архивировано 3 марта 2016 года.
- ↑ Skeptic.net (недоступная ссылка). Были ли американцы на Луне?. Архивировано 14 марта 2016 года.
- ↑ [dic.academic.ru/searchall.php?SWord=%D0%B8%D1%81%D1%82%D0%B8%D0%BD%D0%BD%D1%8B%D0%B9+%D0%B3%D0%BE%D1%80%D0%B8%D0%B7%D0%BE%D0%BD%D1%82&stype=0 Словари и энциклопедии на Академике]. Толкования выражения «истинный горизонт». Архивировано 3 февраля 2012 года.
- ↑ Запаренко Виктор. Большая энциклопедия рисования Виктора Запаренко. — М.: АСТ, 2007. — 240 с. — ISBN 978-5-17-041243-3.
- ↑ Истина и метод. С.358
Литература
- Витковский В. В. Горизонт // Энциклопедический словарь Брокгауза и Ефрона : в 86 т. (82 т. и 4 доп.). — СПб., 1890—1907.
- Горизонт // Большая советская энциклопедия : [в 30 т.] / гл. ред. А. М. Прохоров. — 3-е изд. — М. : Советская энциклопедия, 1969—1978.