Асимптотически параллельные прямые

Две прямые через заданную точку P, асимптотически параллельные прямой R.

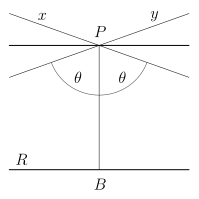
В нейтральной или абсолютной геометрии и в геометрии Лобачевского могут иметься много прямых, параллельных данной прямой [math]\displaystyle{ R }[/math] и проходящих через точку [math]\displaystyle{ P }[/math] вне этой прямой. Однако две параллельные могут быть ближе к [math]\displaystyle{ R }[/math], чем остальные (по одной с каждой стороны).

Имеет смысл в этом случаен дать другое определение параллельности для нейтральной геометрии. Если имеются очень близкие параллельные к данной прямой, их называют асимптотически параллельными или параллельными в пределе.

Для лучей отношение асимптотической параллельности является отношением эквивалентности, которое включает терминальное отношение эквивалентности.

Асимптотические параллельные могут образовывать две или три стороны асимптотического треугольника.

Определение

Луч Aa является асимптотически параллельным лучу Bb, что записывается как [math]\displaystyle{ Aa|||Bb }[/math]

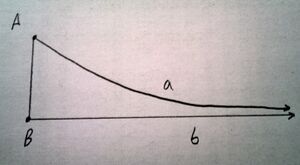
Луч [math]\displaystyle{ Aa }[/math] является асимптотически параллельным лучу [math]\displaystyle{ Bb }[/math], если они котерминальны или если они лежат на различных прямых, не равных прямой [math]\displaystyle{ AB }[/math], не пересекаются и любой луч внутри угла [math]\displaystyle{ BAa }[/math] пересекает луч [math]\displaystyle{ Bb }[/math].

Свойства

Различные прямые, содержащие асимптотические параллельные лучи, не пересекаются.

Доказательство

Предположим, что прямые, содержащие различные параллельные лучи, пересекаются. По определению они не могут пересечься на стороне [math]\displaystyle{ AB }[/math], в которой находится луч [math]\displaystyle{ a }[/math]. Тогда они должны пересекаться на стороне [math]\displaystyle{ AB }[/math], противоположной лучу [math]\displaystyle{ a }[/math], обозначим эту точку [math]\displaystyle{ C }[/math]. Тогда (здесь P = прямой угол) [math]\displaystyle{ \angle CAB + \angle CBA \lt 2P \Rightarrow \angle aAB + \angle bBA \gt 2P }[/math]. Противоречие.

См. также

• Орицикл, в геометрии Лобачевского кривая, нормали которой асимптотически параллельны
• Угол параллельности