N-Hash

N-Hash
Создан	1990
Опубликован	1990
Размер хеша	128 бит
Число раундов	12 или 15
Тип	хеш-функция

N-Hash — криптографическая хеш-функция на основе циклической функции FEAL. В настоящее время считается небезопасной.

Была разработана в 1990 году фирмой Nippon Telegraph and Telephone (также разработавшей FEAL).

Изначально, функция N-Hash была предназначена для того, чтобы решить проблему подмены информации на пути между двумя пользователями телефонной связи (Nippon Telegraph and Telephone — телекоммуникационная компания) и ускорить поиск данных. Например, если человек посылает смс-сообщение, то перед доставкой оно будет проверено на подлинность с помощью хеш-функции. А если пользователю продукции Nippon Telegraph and Telephone надо быстро найти в телефоне чей-либо контакт, то с помощью N-Hash можно упростить процесс поиска имени в списке. Это осуществляется благодаря тому, что хеш-кодом (маленькой по объёму определяющей частью контакта) имени объявляется первая буква контакта.

История возникновения

В основе алгоритма N-Hash лежит блочный алгоритм шифрования FEAL. Крупнейшая телекоммуникационная компания Nippon Telegraph and Telephone создала FEAL на основе DES. Но хотя этот алгоритм и выигрывает в быстродействии у DES, он является очень ненадежным и легко уязвимым: криптоаналитику требовалось очень мало информации, чтобы взломать алгоритм. Именно взлом алгоритма FEAL повлек за собой появление хеш-функции N-Hash в 1990 году. N-Hash также выигрывает в скорости у DES: по сравнению с 9 Кбит/сек у DES, N-Hash работает со скоростью 24 Кбит/сек для 15-раундовой схемы и со скоростью 29 Кбит/сек для 12-раундовой. При этом Nippon Telegraph and Telephone добилась повышения надёжности по сравнению с FEAL.

В течение некоторого времени алгоритм N-Hash использовался фирмой Nippon Telegraph and Telephone в соответствии с целями данной функции, но через некоторое время был разработан метод дней рождения, который с лёгкостью взламывал этот алгоритм. В связи со взломом отказались не только от N-Hash, но и почти от всех функций, основанных на блочных шифрах, так как для всех них характерна одна и та же проблема: они легко уязвимы методом дней рождения. Вместо них теперь используют более надежные функции, основанные на MD — технологиях: MD5, SHA-1 и другие, приведенные в списке функций, которые на данный момент считаются надежными (согласно стандарту ISO/IEC 10118).

Использование

Функция N-Hash использовалась в течение недолгого времени в начале 1990-х годов, пока не была взломана методом дней рождения.

• N-Hash предназначалась для решения проблемы подмены данных:
  • Для современного человека эта проблема может легко быть описана на примере взаимодействия человека и интернет-магазина. Когда пользователь заказывает какой-нибудь товар в интернет-магазине, то магазин присылает ему номер заказа, сумму платежа и т. д. Далее, когда пользователь пытается оплатить заказ с помощью, например, Webmoney, то Webmoney вычисляет хеш-код полученного сообщения и сравнивает его с хеш-кодом, полученным от интернет-магазина. Если эти хеш-коды совпадают, то информация, присланная пользователем, правдива. Если не совпадают, то информация определяется как ложная и платеж не проходит.
• Другой вариант использования прост: упорядочивание контактов в мобильном телефоне по алфавиту и поиск контакта по первой букве. Хеш-кодом имени выбирается первая буква этого имени, следовательно, когда человек нажимает некоторую букву в своем телефоне, то ищется хеш-код, который совпадает с этой буквой и на экран выводятся контакты, начинающиеся с неё.

Особенности N-Hash

Однонаправленность

Определение: Пусть [math]\displaystyle{ M }[/math] — сообщение некоторой длины.

Функция [math]\displaystyle{ H }[/math] называется однонаправленной, если из равенства [math]\displaystyle{ h=H(M) }[/math]

легко:

• найти хеш-код [math]\displaystyle{ h }[/math], зная сообщение [math]\displaystyle{ M }[/math]

очень трудоёмко:

• найти сообщение [math]\displaystyle{ M }[/math] по известному хеш-коду [math]\displaystyle{ h }[/math] (т. е. если хеш-код пароля стал известен хакеру, то пароль он по нему не найдет);
• найти отличное от [math]\displaystyle{ M }[/math] сообщение [math]\displaystyle{ M' }[/math], такое что их хеш-коды [math]\displaystyle{ H(M')=H(M) }[/math] совпадают.

Проще определение можно записать так:

Однонаправленность — это «отпечаток пальца»:

• Если дан конкретный человек, то можно взять у него отпечаток пальца;
• Невозможно найти человека по отпечатку его пальца (если нет базы данных с отпечатками пальцев всех людей, а её нет);
• Невозможно найти второго человека с таким же как у другого отпечатком пальца.

Однонаправленность решает очень важную проблему. Рассмотрим её на примере.

Алиса и Боб традиционно обозначают субъектов передачи информации.

Примеры

• Допустим, Алиса подписала контракт [math]\displaystyle{ M }[/math] с известным Алисе и Бобу хеш-кодом [math]\displaystyle{ h=H(M) }[/math]. Если бы [math]\displaystyle{ H }[/math] была неоднонаправленная, то Боб мог бы найти такой другой контракт [math]\displaystyle{ M' }[/math], что [math]\displaystyle{ H(M')=H(M) }[/math] и, значит, смог бы утверждать, что Алиса подписала [math]\displaystyle{ M' }[/math].
• Допустим, Алиса имеет один и тот же отпечаток пальца h с каким-нибудь преступником, тогда Боб смог бы утверждать, что этот преступник — Алиса.

Устойчивость к столкновениям

Чтобы предотвратить возможность Алисы использовать метод «дней рождения» для обмана Боба, очень удобно ввести ещё более сильное условие, чем условие однонаправленности. H такова, что трудно найти сообщения [math]\displaystyle{ M }[/math] и [math]\displaystyle{ M' }[/math], такие что их хеш-коды [math]\displaystyle{ H(M)=H(M') }[/math] совпадают. То есть невозможно найти двух человек с одинаковыми отпечатками пальцев.

Данное условие называется устойчивостью к столкновениям и для хеш-функции N-Hash оно не выполняется.

По причине неустойчивости к столкновениям Алиса может обмануть Боба таким образом (метод «дней рождения»):

• Алиса пишет две версии контракта: одна из них выгодна для Боба, а другая нет;
• Внося небольшие изменения в каждый контракт (например, пробел заменяет на два пробела), она добьется того, что версий контрактов будет достаточно много для подбора [math]\displaystyle{ M }[/math] и [math]\displaystyle{ M' }[/math], для которых совпадают хеш-коды (версия [math]\displaystyle{ M }[/math] выгодна Бобу, а [math]\displaystyle{ M' }[/math] — нет) (если в контракте 34 строки, то, внося или не внося изменения в каждую из строк, легко получить [math]\displaystyle{ 2^{34} }[/math] версий контрактов);
• Теперь Алиса сможет доказать, что Боб подписал [math]\displaystyle{ M' }[/math].

Для того, чтобы избежать подобной проблемы, достаточно вносить косметические изменения в подписываемый контракт. И хотя это действие никак не изменяет хеш-функцию H, а, значит, никак не влияет на её устойчивость к столкновениям, но человек этим действием получит новую версию контракта, хеш-код которого не совпадает с хеш-кодом версии контракта злоумышленника. То есть, если Боб в 5-й строке поставит в каком-нибудь месте запятую, или поставит две точки вместо одной, то Алиса не сможет доказать, что он подписал другой контракт (так как его хеш-код уже не совпадает с хеш-кодом контракта Алисы).

Можно рассмотреть жизненный пример: когда нотариус ставит печать в подписываемый контракт, он вносит туда косметические изменения.

Цели N-Hash

Для того, чтобы понять как работает функция N-Hash, необходимо перейти на более научную речь. Ниже приведены цели данной функции не на примерах, а в соответствии с тем, как они осуществляются и с соответствующей терминологией.

• Обеспечение целостности информации:

Данное свойство необходимо для того, чтобы исключить возможность злоумышленника внедрить некоторую ложную информацию в исходное сообщение. Для обеспечения целостности должна быть возможность обнаружить любые изменения в тексте сообщения (замена, вставка, удаление). Целостность обеспечивается путём внедрения в исходное сообщение избыточной информации, которая будет являться проверочной комбинацией. Такая комбинация называется контрольной суммой и её можно вычислить с помощью специального алгоритма. Так как этот алгоритм зависит от секретного ключа, то внедрение ложной информации в сообщение маловероятно.

[math]\displaystyle{ M_{new}=M+''salt'' }[/math], где salt — избыточная информация, M — сообщение [math]\displaystyle{ H(salt)=S }[/math]- контрольная сумма;

Из формулы следует, что если меняется salt, то меняется и S (контрольная сумма), а значит изменялось и [math]\displaystyle{ M_{new} }[/math] и [math]\displaystyle{ M }[/math].

То есть можно сделать вывод, что была добавлена ложная информация.

• Сжатие документа:

Функция N-Hash работает с сообщениями M произвольной длины. При этом на выходе получается хеш-код фиксированной длины в 128 бит. Это получается за счет того, что сообщение делится на блоки [math]\displaystyle{ M_{i} }[/math], размером 128 бит, и алгоритм работает последовательно с каждым из блоков.

• Обеспечение достоверности электронных данных:

Данное свойство выполняется для однонаправленных функций, какой и является N-Hash. Достоверность сообщения M проверяется путём нахождения конечного хеш-кода (дайджеста сообщения) дважды (отсылающая и принимающая стороны). Результаты сравниваются и, если они совпадают, то информация достоверна. Целостность не гарантирует достоверность.

• Обеспечение конфиденциальности:

на сайтах, где нужно вводить логин и пароль, пароль после ввода переводится в хеш-код. То есть изначально пользователь вводит пароль M, но для входа в защищённую область используется хеш-код [math]\displaystyle{ h=H(M) }[/math]. По известному хеш-коду h и функции H вычислить M очень трудно, чем и обеспечивается конфиденциальность пароля.

• Аутентификация пользователей:

Аутентификация — это процедура проверки подлинности пользователя или данных при помощи некоторого критерия.

Возникает вопрос, как хеш-функция обеспечивает правдивость аутентификации. Это легко показать на примере.

Когда пользователь вводит логин и пароль на каком-либо сайте, его пароль преобразуется в хеш-код и передается по сети для аутентификации. Очевидно, что для того чтобы войти под чужую учётную запись достаточно выяснить хеш-код пароля, а затем по формуле [math]\displaystyle{ h=H(M) }[/math] (h-хеш-код, M — пароль) найти пароль. Но N-Hash, являющаяся однонаправленной функцией, обеспечивает сохранность пароля, так как это уравнение для однонаправленных функций решается очень трудоёмко (не с помощью персонального компьютера).

Алгоритм

Алгоритм N-Hash основан на циклическом повторении (12 или 15 раз — число раундов) операций. На входе имеется хеш-код [math]\displaystyle{ h_{0} }[/math] и он может быть произвольным, на выходе получается хеш-код h сообщения M, которое необходимо хешировать. При этом размер выходящего хеш-кода фиксирован и равен 128 бит, тогда как размер M произволен.

Основные обозначения

• [math]\displaystyle{ M }[/math] — сообщение, которое необходимо хешировать;
• [math]\displaystyle{ M_{i} }[/math] — блок сообщения длиной 128 бит. Для того, чтобы хешировать сообщение [math]\displaystyle{ M }[/math] необходимо поделить его на блоки [math]\displaystyle{ M_{i} }[/math];
• [math]\displaystyle{ h_{i} }[/math] — хеш-код i-го шага;
• [math]\displaystyle{ \nu=1010...1010 }[/math] — константа, длиной 128 бит;
• [math]\displaystyle{ || }[/math] — конкатенация;
• [math]\displaystyle{ V_{j}=\delta||A_{j1}||\delta||A_{j2}||\delta||A_{j3}||\delta||A_{j4} }[/math], где [math]\displaystyle{ A_{jk}=4*(j-1)+k }[/math], где k=1, 2, 3, 4; [math]\displaystyle{ \delta=00..00 }[/math], длиной 24 бит;
• EXG — функция, которая меняет местами старшие и младшие разряды (64 младших и 64 старших);
• PS — преобразующая функция;

Описание алгоритма

На схеме справа представлены схематические обозначения операций, которые присутствуют на нижеследующих схемах.

• Покоординатное (попарное) суммирование означает сложение по модулю 2;
• Если x поступает на вход функции f, то на выходе получается f(x).

Один цикл работы N-Hash

один цикл работы N-Hash

Ниже представлен один цикл работы алгоритма N-Hash.

• На вход функции g подается хеш-код (i-1)-го шага [math]\displaystyle{ h_{i-1} }[/math] и i-й блок сообщения [math]\displaystyle{ M_{i} }[/math]. При этом [math]\displaystyle{ h_{0} }[/math] выбирается произвольно: например, он может быть нулевым. А также [math]\displaystyle{ h_{i-1} }[/math] подается на выход на операцию сложения по модулю 2, то есть результат (хеш-код следующего шага) будет выглядеть так: [math]\displaystyle{ h_{i-1}\oplus }[/math](нечто пока неизвестное).
• Из схемы видно, что [math]\displaystyle{ M_{i} }[/math] подается не только на XOR, но и на выход на операцию сложения по модулю 2. То есть теперь в соответствии с первым пунктом результат выглядит таким образом: [math]\displaystyle{ h_{i-1}\oplus M_{i} }[/math](оставшееся пока неизвестным нечто).

Оставшееся пока неизвестным нечто находится после прохождения каскада из восьми преобразующих функций. Его получение может быть описано таким образом:

• Функция EXG меняет местами старшие и младшие разряды [math]\displaystyle{ h_{i-1} }[/math] и прибавляет к результату [math]\displaystyle{ \nu }[/math], после чего результат складывает по модулю 2 с [math]\displaystyle{ M_{i} }[/math].
• Как видно из схемы, результат подается последовательно на входы j преобразующих функций, вторым аргументом которых является сумма [math]\displaystyle{ h_{i-1}\oplus V_{j} }[/math], где j=1, … , 8.
• В результате получается хеш-код i-го шага [math]\displaystyle{ h_{i} }[/math]:

[math]\displaystyle{ h_{i}=M_{i}\oplus g(M_{i}, h_{i-1})\oplus h_{i-1} }[/math].

Преобразующая функция

Схема преобразующей функции. Каждый из аргументов разбивается на 4 блока по 32 бит каждый.

Возникает вопрос, как действует преобразующая функция [math]\displaystyle{ PS(X, P) }[/math].

Рассмотрим верхнюю часть схемы до перекрестья.

Исходное сообщение [math]\displaystyle{ X }[/math] разбивается на блоки по [math]\displaystyle{ 128/4=32 }[/math] бита.

Будем считать промежуточными выходами входы в нижнюю часть схемы. [math]\displaystyle{ X_{1} }[/math] и [math]\displaystyle{ X_{2} }[/math] подаются на промежуточные выходы, а на два других выхода подаются операции [math]\displaystyle{ f(X_{1}, P_{1})\oplus X_{2}\oplus X_{4} }[/math] и [math]\displaystyle{ f[f(X_{1}, P_{1})\oplus X_{2}, P_{2}]\oplus X_{1}\oplus X_{3} }[/math]. Теперь можно результаты на промежуточных выходах переобозначить и через них, аналогично верхней части, найти результаты на выходе нижней части, то есть и всей схемы в целом.

Сделав все необходимые вычисления, получим, что при подаче на вход [math]\displaystyle{ {X=X_{1}\parallel X_{2}\parallel X_{3}\parallel X_{4}} }[/math] сообщение на выходе [math]\displaystyle{ {Y=Y_{1}\parallel Y_{2}\parallel Y_{3}\parallel Y_{4}} }[/math] можно представить как конкатенацию сообщений

• [math]\displaystyle{ {Y_{4}=X_{2}\oplus X_{4}\oplus f(X_{1}, P_{1})} }[/math];
• [math]\displaystyle{ {Y_{3}=f[f(X_{1}, P_{1})\oplus X_{2}, P_{2}]\oplus X_{1}\oplus X_{3}} }[/math];
• [math]\displaystyle{ {Y_{2}=X_{2}\oplus Y_{4}\oplus f(Y_{3}, P_{3})} }[/math];
• [math]\displaystyle{ {Y_{1}=f[f(Y_{3}, P_{3})\oplus Y_{4}, P_{4}]\oplus X_{1}\oplus Y_{3}} }[/math].

Поиск функции f(x, P)

Схема поиска функции f(x ,P)

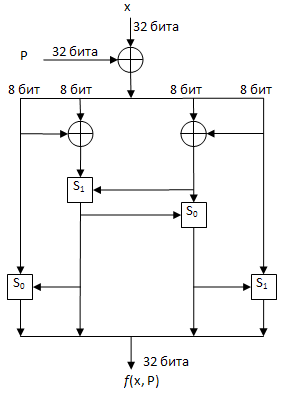
Так как функция f работает с аргументами, длина которых составляет 32 бит, то из схемы поиска функции f(x, P) имеем:

• Величину [math]\displaystyle{ x\oplus P }[/math] разбиваем на части по 8 бит.
• Запишем эти части как [math]\displaystyle{ x_{i}\oplus P_{i} }[/math], i=1,…,4 и введёт новые обозначения:
  • [math]\displaystyle{ {Z_{1}=x_{1}\oplus P_{1}} }[/math];
  • [math]\displaystyle{ {Z_{2}=x_{2}\oplus P_{2}} }[/math];
  • [math]\displaystyle{ {Z_{3}=x_{3}\oplus P_{3}} }[/math];
  • [math]\displaystyle{ {Z_{4}=x_{4}\oplus P_{4}} }[/math];

Аргументами функции [math]\displaystyle{ {S_{0}} }[/math] (первая стрелка слева) являются [math]\displaystyle{ Z_{1} }[/math] и [math]\displaystyle{ {S_{1}[Z_{1}\oplus Z_{2}, Z_{3}\oplus Z_{4}]} }[/math].

Аргументами функции [math]\displaystyle{ {S_{1}} }[/math] (вторая стрелка слева) являются [math]\displaystyle{ {Z_{1}\oplus Z_{2}} }[/math] и [math]\displaystyle{ {Z_{3}\oplus Z_{4}} }[/math].

То есть две составляющие части из сообщения на выходе уже известны и равны

• • [math]\displaystyle{ {A_{1}=S_{0}(Z_{1}, S_{1}[Z_{1}\oplus Z_{2},Z_{3}\oplus Z_{4}])} }[/math];
  • [math]\displaystyle{ {A_{2}=S_{1}[Z_{1}\oplus Z_{2}, Z_{3}\oplus Z_{4}]} }[/math];

Далее будем пользоваться уже полученными оставляющими частями сообщения на выходе для удобства записи:

• • [math]\displaystyle{ {A_{3}=S_{0}[Z_{3}\oplus Z_{4}, A_{2}]} }[/math];
  • [math]\displaystyle{ {~A_{4}=S_{1}[Z_{4}, A_{3}]} }[/math];

• Тогда сообщение на выходе можно представить в виде [math]\displaystyle{ {A=A_{1}||A_{2}||A_{3}||A_{4}} }[/math].

• Причём известно, что
  • [math]\displaystyle{ {S_{0}} }[/math]=(левый циклический сдвиг на 2 бита)(a+b) mod 256
  • [math]\displaystyle{ {S_{1}} }[/math]=(левый циклический сдвиг на 2 бита)(a+b+1) mod 256

Безопасность хеш-функций

Хеш-функция является безопасной в случае, когда криптоаналитику требуется очень много информации, для того чтобы взломать данную хеш-функцию (что делает взлом маловероятным) и если хеш-функция не взломана к данному времени.

Для того, чтобы хеш-функция была безопасной, необходимо, чтобы выполнялись условия:

• При изменениях в тексте сообщения [math]\displaystyle{ M }[/math] (вставки, перестановки и т. д.) должен меняться и хеш-код сообщения;

Иначе человек, который вводит свои логин и пароль для входа в Википедию, мог бы попасть на страницу другого участника.

• Невозможность нахождения сообщения [math]\displaystyle{ M }[/math] по известному хеш-коду [math]\displaystyle{ h }[/math] из [math]\displaystyle{ h=H(M) }[/math];

Если данное условие не выполняется, то это делает возможным нахождение паролей пользователей Википедии.

• Задача нахождения сообщений [math]\displaystyle{ M_{1} }[/math] и [math]\displaystyle{ M_{2} }[/math], таких что их хеш-коды равны [math]\displaystyle{ h_{1}=h_{2} }[/math] должна быть очень трудоёмкой.

Иначе, можно было бы найти два пароля с одинаковыми хеш-кодами.

N-Hash не является безопасной функцией, так как для неё не выполнено последнее условие.

Криптоанализ N-Hash

В настоящее время N-Hash считается небезопасной функцией. На данном рисунке указаны все безопасные однонаправленные функции на данный момент согласно стандарту ISO/IEC 10118:

Из алгоритмов, построенных как и N-Hash на основе блочных шифров, безопасными считаются только MDC-2 и MDC-4.

Для N-Hash характерна следующая проблема:

• Так как длина хеш-кода равна длине блока алгоритма шифрования, то алгоритм нестоек перед атакой методом «дней рождения».

Атаки на хеш-функции

На данном рисунке приведена классификация атак на все алгоритмы хеширования в целом.

Атаки, зависящие от алгоритма, являются атаками, основанными на свойствах конкретного алгоритма.

Например, N-Hash успешно атакуют с помощью дифференциального метода, атакой с фиксированной точкой и встречей посередине.

Атаки, не зависящие от алгоритма, можно применить к любой функции хеширования, однако это не исключает того, что для некоторых алгоритмов они очень трудоёмки из-за большого объёма информации или быстродействия кода.

Действенные атаки на N-Hash

• Полный перебор
• Метод встречи в середине атаки
• Парадокс дня рождения
• Дифференциальный криптоанализ
• Атака с фиксированной точкой

Атаки, базирующиеся на уязвимости алгоритма

Дифференциальный метод

Ден Бур предложил способ построения коллизии для однораундовой схемы N-Hash.

Бихам и Шамир успешно применили метод дифференциального криптоанализа для компрометации 6-раундовой схемы N-Hash. Предложенный ими способ построения коллизии срабатывает для любого значения N кратного трём и при этом для N ≤ 12 он оказывается эффективнее подхода, основанного на парадоксе дней рождения.

Для 12-раундовой схемы сложность построения коллизий предложенным методом оценивается величиной 256 операций (трудоёмкость метода, основанного на парадоксе дней рождения — 264 операций).

Атаки, не зависящие от алгоритма

Увеличение длины хеш-кода и секретного ключа усложнит работу криптоаналитика. Можно попытаться сделать вычисления слишком трудоёмкими для персонального компьютера и требующими больших ресурсов. Тогда криптоаналитику надо будет или искать суперкомпьютер, или написать вирус, который на основе распараллеливания процесса взлома хеш-функции будет использовать сразу несколько персональных компьютеров для решения проблемы.

Также действенны такие методы защиты хеш-функции:

• использование контрольных сумм на разных этапах хеширования;
• проверка на достоверность информации;
• внедрение в сообщение информации типа salt.

Итоги

• В настоящее время N-Hash мало распространён, так как не является безопасным и взломан более 10 лет назад.
• Теперь для хеш-функций типа N-Hash существует специальное название — ключевые, то есть однонаправленные, но не устойчивые к столкновениям:
  • Если стороны доверяют друг другу (то есть каждая из сторон уверена, что другая не станет подменять контракт как в случае с Алисой и Бобом), то можно использовать N-Hash.

Сравнение N-Hash с другими хеш-функциями

Алгоритм	Длина хеш-значения	Скорость шифрования (Кбайт/сек)
Одновременная схема Davies-Meyer (c IDEA)	128	22
Davies-Meyer (с DES)	64	9
Хеш-функция ГОСТ	256	11
HAVAL (3 подхода)	переменная	168
HAVAL (4 подхода)	переменная	118
HAVAL (5 подходов)	переменная	98
MD2	128	23
MD4	128	236
MD5	128	174
N-Hash (12 этапов)	128	29
N-Hash (15 этапов)	128	24
RIPE-MD	128	182
SHA-1	160	75
Snefru (4 прохода)	128	48
Snefru (8 подходов)	128	23

См. также

• Хеширование
• Коллизия хеш-функции
• FEAL

Ссылки

• Современное хеширование
• Аутентификация данных и электронная цифровая подпись

Литература

• А. Щербаков, А. Домашев. Прикладная криптография. — М.: Русская Редакция, 2003. — 404 с. — ISBN 5-7502-0215-1.
• Брюс Шнайер. Прикладная криптография. — 2-е изд. — М.: Триумф, 2002. — 816 с.