Mx-магнитометр
Mx-магнитометр — наиболее распространённый вид оптического квантового магнитометра, работающего на парах щелочных металлов (цезия, рубидия, калия).
Принцип работы
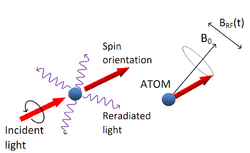
Падающий свет круговой поляризации возбуждает атом из основного состояние в возбужденное. Полученная атомом энергия расходуется в виде переизлученного спонтанного света и на создание макроскопического спина, который прецессирует вокруг магнитного поля [math]\displaystyle{ B_0 }[/math]
При комнатной температуре тепловая энергия [math]\displaystyle{ kT }[/math] атомов намного больше разницы энергий [math]\displaystyle{ \Delta E }[/math] основного состояния — [math]\displaystyle{ (kT\ll \Delta E) }[/math], поэтому согласно распределению Больцмана населённости всех уровней одинаковы, см. схему атомов рубидия Rb87. При взаимодействии атомов с оптическим полем круговой поляризации [math]\displaystyle{ \sigma^{+} }[/math] в атомном газе создается неравновесное распределение населённости атомов по зеемановским подуровням основных состояний. В результате атомный газ поляризуется и у него появляется магнитный момент [math]\displaystyle{ \mu }[/math].
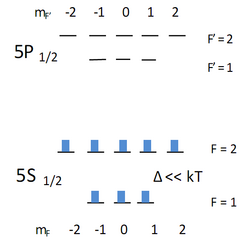
[math]\displaystyle{ 5S_{1/2}, 5P_{1/2} }[/math] — Основное и возбужденное состояния рубидия
Синии прямоугольники показывают распределение населённостей на разных зеемановских подуровнях.
Известно, что магнитный момент, помещённый в постоянное магнитное поле [math]\displaystyle{ B_{o} }[/math] начинает прецессировать с частотой [math]\displaystyle{ \omega_{L}=\gamma B_{o} }[/math]. Такое поведение [math]\displaystyle{ \mu }[/math] описывается уравнениями Блоха.

Красные стрелки — резонансный свет круговой поляризации, длина волны 794,5 нм [math]\displaystyle{ \sigma^+ }[/math].
Синие прямоугольники показывают распределение населенностей на разных зеемановских подуровнях.
Зеленые кривые — действие радиочастотного поля [math]\displaystyle{ B_{RF}(t) }[/math]
В Мх-магнитометре лазерный луч распространяется под углом 45 градусов по отношению к направлению измеряемому магнитному полю [math]\displaystyle{ B_{o} }[/math]. Кроме поля [math]\displaystyle{ B_o }[/math], перпендикулярно к нему приложено также небольшое осциллирующее поле [math]\displaystyle{ B_{RF}(t) }[/math]. Это поле [math]\displaystyle{ B_{RF}(t) }[/math] навязывает фазу прецессирующих вокруг поля Во на частоте [math]\displaystyle{ \omega_L }[/math] магнитного момента атомов (спинов). Проекция магнитного момента на направление распространения света прецессирующей поляризации будет оставаться постоянной до момента включения поля [math]\displaystyle{ B_{RF}(t) }[/math]. Включение этого поля приведёт к изменению населённости между зеемановскими подуровнями и, как следствие, это поле вызовет модуляцию поглощения проекции магнитного момента [math]\displaystyle{ B_1 }[/math], которое регистрируется фотодетектором, затем усиливается, фазовращателем корректируется фаза сигнала, и подаётся на радиочастотную катушку. Таким образом создается петля положительной обратной связи. Подобрав фазу сигнала добиваются генерации поля на частоте Ларморовской прецессии [math]\displaystyle{ \omega_L }[/math]. Эта частота измеряется с помощью частотомера и по её величине определяют величину магнитного поля.
Чувствительность магнитометра
Чувствительность магнитометра [math]\displaystyle{ \delta B }[/math] определяется соотношением [math]\displaystyle{ \delta B = \frac{\kappa}{\gamma}\frac{N \Gamma}{S}, }[/math] где [math]\displaystyle{ \Gamma }[/math] — ширина магнитного резонанса, [math]\displaystyle{ S }[/math]- его амплитуда, [math]\displaystyle{ \gamma }[/math] — гиромагнитное отношение, [math]\displaystyle{ N }[/math]- среднеквадратичный уровень шумов, усредненных за время [math]\displaystyle{ \tau }[/math], [math]\displaystyle{ \kappa }[/math] — форм фактор резонанса приблизительно равный 1. В случае преобладания дробовых шумов в фототоке детектора эта формула принимает вид[1]
[math]\displaystyle{ \delta B^{short}= \kappa \frac{\Gamma}{\gamma} \frac{\rho}{S} \frac{1}{\sqrt{2\pi\tau}} }[/math]
[math]\displaystyle{ \rho }[/math] — плотность дробового шума , В случае преобладания квантовых шумов в фототоке детектора она выглядит так:
[math]\displaystyle{ \delta B^{quant}= \frac{1}{\gamma}\frac{1}{\sqrt {N_a {T_2}\tau}} }[/math]
[math]\displaystyle{ T_2 }[/math] — поперечное время релаксации поляризации атома
Резонансный свет лазера (Light source) накачивает атомы на уровни основного состояния [math]\displaystyle{ 5S_{1/2}, F=2 }[/math]. Линейную поляризацию света лазера с помощью фазовой пластины [math]\displaystyle{ \lambda/4 }[/math] превращают в круговую [math]\displaystyle{ \sigma^{+} }[/math]. Благодаря этому неравновесная населенность зеемановских подуровней аккумулируется на уровнях с большой проекцией момента [math]\displaystyle{ m_F }[/math]. Вектор распространения света и направление измеряемого магнитного поля [math]\displaystyle{ B_o }[/math] повёрнуты относительно друг друга на угол 45 градусов (синяя стрелка). Перпендикулярно полю [math]\displaystyle{ B_o }[/math] включается радиочастотное поле [math]\displaystyle{ B_{RF}(t) }[/math]. Пропускание прошедшего через ячейку света модулируется этим полем и регистрируется фотодиодом.
Модуляция света полем [math]\displaystyle{ B_{RF}(t) }[/math] происходит благодаря двум процессам: за счёт изменения поглощения из-за переноса населённости с одного зеемановского подуровня на другой и благодаря модуляции вероятности взаимодействия света с атомом за счёт создания между ними квантовой когерентности.
Ширина резонанса определяется различными релаксационными процессами[2]:
- столкновениями со стенками ячейки, с молекулами буферных газов, и атом- атом столкновениями
- полевым уширением, вызываемым как оптическим, так и радиочастотным полями;
- конечным временем взаимодействия с оптическим полем, определяемым пролётом атомов через сечение оптического поля

Примечания
- ↑ S. Groeger, G. Bison, J.-L. Schenker, R. Wynands, and A. Weis, Eur. Phys. J. D 38, 239—247 (2006), DOI: 10.1140/epjd/e2006-00037-y THE EUROPEAN PHYSICAL JOURNAL D , A high-sensitivity laser-pumped Mx-magnetometer,
- ↑ А. К. Вершовский, Новые квантовые радиооптические системы и методы измерения слабых магнитных полей, диссертация на соискание ученой степени доктора физико-математических наук, Институт им. А. Ф. Иоффе, Санкт Петербург, 2007 г.
Литература
- Georg Bison, Development of an optical cardio-magnetometer chapter 2. Optimization and performance of an optical cardiomagnetometer, der Mathematisch-Naturwissenschaftlichen FakultÄat der UniversitÄat Freiburg in der Schweiz, Nummer der Dissertation: 1450 UniversitÄatsdruckerei Freiburg, 2004
- D. Budker, W. Gavlik, D.F. Kimball, S.M. Rochester, V.V. Yashuchuk, and A. Weis, Resonant nonlinear magneto-optical effects in atoms, Review of Modern Physics, V. 74 1153—1201 (2002)
- Dmitry Budker and Michael Romalis, Optical magnetometry, Nature physics, v.3 227—234 (2007)
- S.Groeger, G. Bison, J.-L. Schenker. R. Wynands, and A. Weis, A high-sensitivity laser-pumped Mx magnetometer, Eur. Phys. J. D, v. 38, 239—247 (2006)
- Optical Magnetometry. editors: Dmitry Budker, Derek F. Jackson Kimball,
Cambridge University Press, PUBLISHED: April 2013, ISBN 9781107010352