HDCP

Не следует путать с DHCP.

HDCP (англ. High-bandwidth Digital Content Protection — «защита широкополосного цифрового содержимого») — технология защиты медиаконтента, разработанная корпорацией Intel и предназначенная для предотвращения незаконного копирования высококачественного видеосигнала, передаваемого через интерфейсы DVI (для этого интерфейса HDCP является необязательной опцией), DisplayPort (для этого интерфейса HDCP является необязательной опцией), HDMI, GVIF или UDI. Защищённый видеосигнал может быть воспроизведён только на оборудовании, поддерживающем HDCP.

Система шифрования HDCP версий 1.x была окончательно взломана в 2010 году (был восстановлен мастер-ключ системы).

Технология

HDCP создана для защиты передачи медиаконтента между HDCP-передатчиком и HDCP-приёмником. Технология также предусматривает использование HDCP-повторителей с защищёнными портами для нисходящего потока данных (от поставщика к заказчику услуги). В системе может быть до семи уровней HDCP-повторителей и до 128 HDCP-совместимых устройств.

Система защиты состоит из трёх основных компонентов:

• Протокол аутентификации
• Шифрование передаваемых данных
• Защита от подслушивания «третьим лицом»

Нахождение секретной матрицы DCP LLC

14 сентября 2010 несколько онлайн СМИ (ZDNet, Engadget) сообщили о факте открытой публикации мастер-ключа HDCP, с помощью которого можно создавать закрытые ключи устройств HDCP (device private keys) без помощи со стороны оператора ключевой инфраструктуры HDCP (The Digital Content Protection LLC). C публикацией мастер-ключа были нейтрализованы все меры по отзыву ключей устройств, так как вместо старого (отозванного) ключа устройства всегда можно сгенерировать новый. Не вполне ясно, каким образом был получен мастер-ключ, известно, что публикация ключа вместе с инструкцией по использованию произошла через Twitter и pastebin. Engadget считает, что атакующий мог использовать метод Crosby (2001).

Через 2 дня, 16 сентября, компания Intel (создатель HDCP) подтвердила, что данный мастер-ключ реален и что защита HDCP фактически взломана. Intel угрожает, что предпримет юридические действия против любого, кто изготавливает аппаратные устройства для обхода защиты HDCP.

Протокол аутентификации

Протокол аутентификации используется между HDCP-передатчиком и HDCP-приёмником для подтверждения того, что последний является устройством, которому разрешено получать соответствующий контент. Подтверждение — знание секретного набора ключей. Каждое HDCP-устройство снабжается уникальным набором из сорока 56-битных секретных ключей, называемых DPK (англ. device private keys, секретные ключи устройства), получаемых от организации DCP LLC. Во время обмена информацией устройства создают общий секрет, который нельзя подслушать во время этого обмена, и этот секрет далее применяется как симметричный ключ для расшифровки HDCP-контента, предназначенного устройству, прошедшему аутентификацию.

Каждое HDCP-устройство хранит, помимо Device Private Keys, соответствующий 40-битный идентификатор — KSV (англ. key selection vector, вектор выбора ключа), который, также как и DPK, получает от DCP LLC.

Протокол аутентификации можно разбить на три части:

• Установление общего секрета
• Сообщение HDCP-повторителя о векторах выбора ключа, присоединённых HDCP-получателях
• Установление начального состояния шифра HDCP для кодирования содержимого кадра (третья часть происходит во время вертикального интервала, который предшествует каждому кадру, требующему шифрования)

Первая часть протокола аутентификации

На рисунке изображена первая часть работы протокола аутентификации. Первым шагом HDCP-передатчик (устройство А) посылает инициирующее сообщение HDCP-приёмнику (устройство B). Сообщение содержит KSV передатчика (Aksv) и 64-битное псевдослучайное число (An) (число генерируется функцией hdcpRngCipher).

Передатчик может начать процедуру проверки подлинности в любой момент, даже если предыдущая только что завершилась.

Вторым шагом HDCP-приёмник отвечает сообщением с KSV приёмника (Bksv) и битом REPEATER (повторитель), который указывает, является ли устройство B повторителем или нет. HDCP-передатчик проверяет, что Aksv содержит ровно 20 нулей и 20 единиц и не находится в чёрном списке.

На этом этапе в обоих устройствах вычисляется общий 56-битный секрет Km и Km’.

Вычисление производится следующим образом:

Из набора DPK суммируются ключи в соответствии с битовым представлением полученного KSV: если бит равен единице, то соответствующий ключ используется. Сложение ключей происходит по модулю [math]\displaystyle{ 2^{56} }[/math] без переполнения.

См. также: Схема Блома

Пример:

Предположим, Bksv равно 0x5A3. В двоичном представлении — 10110100011.
Следовательно, Устройство А складывает свои секретные ключи, стоящие на позициях 0, 1, 5, 7, 8, 10 и рассчитывает общий секрет Km.

Устройство В проделывает аналогичные вычисления, используя собственный набор секретных ключей и вектор выбора, полученный от устройства A, чтобы посчитать Km’.

На третьем шаге применяется функция hdcpBlockCipher для вычисления Ks, M0, R0. Инициирующие величины для работы этой функции — Km (или Km’) и конкатенация бита REPEATER с An (бит REPEATER указывает на то, что HDCP-приёмник поддерживает дальнейшую передачу HDCP-данных, то есть является повторителем).

• Ks — 56-битный сессионный ключ для работы HDCP шифра
• M0 — 64-битная секретная величина, используемая во второй части протокола аутентификации, а также как вспомогательный инициирующий вектор HDCP шифра.
• R0’ — 16-битный ответ, который видеоприёмник посылает HDCP-передатчику в подтверждение успеха обмена сообщениями аутентификации. HDCP-передатчик должен прочитать R0’ не позднее 100 миллисекунд после того как отправлено число Aksv видеоприёмнику, если прошло больше времени, то считывать R0’ нельзя.

Если аутентификация прошла успешно, то R0 = R0’, иначе в большинстве случаев неравны. Далее, при помощи Ri’, получаемых в течение работы третьей части протокола, можно будет обнаружить, что аутентификация прошла неудачно, в том случае, если величина R0 ошибочно указала успех аутентификации.

Вторая часть протокола аутентификации

Вторая часть протокола аутентификации требуется в том случае, если HDCP-приёмник является HDCP-повторителем. HDCP-передатчик выполняет вторую часть протокола только тогда, когда установлен бит REPEATER (повторитель), это значит, что HDCP-приёмник — HDCP-повторитель. Эта часть протокола составляет список всех KSV устройств, подключенных к HDCP-повторителю ниже по уровню: HDCP-защищённые порты HDCP-повторителей, HDCP-приёмники. Этот список представлен в виде непрерывного набора байтов, в котором каждый KSV занимает 5 байт, записанных в прямом порядке.

Общая длина KSV списка = 5 байт * число присоединенных активных HDCP устройств

HDCP-защищённые порты с неактивными HDCP устройствами ничего не добавляют в набор KSV, так же, как и сам HDCP-повторитель, инициирующий создание списка, не добавляет свой KSV в него.

Для того, чтобы добавить KSV-список, полученный от предыдущего HDCP-повторителя, требуется проверка целостности. HDCP-повторитель, запросивший список, вычисляет V и сравнивает его с полученным V’.

V = SHA-1 (список KSV || состояние B || M0)

Где:

• список KSV — битовое представление KSV
• состояние B — битовое представление состояния устройства B (см. таблицу)
• M0 — некоторая секретная величина

Всё битовое представление располагается в прямом порядке.

Если V≠ V’, то проверка на целостность считается неудачной и HDCP-повторитель не должен принимать список. При этом истечет таймер watchdog (сторожевой таймер) и HDCP-передатчик сумеет обнаружить эту ошибку.

Кроме составления списка KSV производится распространение топологической информации (количество и глубина) вверх по дереву устройств до HDCP-передатчика. Количество устройств (англ. device count) рассчитывается как количество всех HDCP-повторителей и приёмников вниз от устройства, которое считает сумму. Глубина (англ. depth) для HDCP-повторителя равна максимальному значения глубины, полученному от нижестоящих в дереве устройств HDCP-повторителю, плюс один. Например, для HDCP-повторителя с четырьмя нижестоящими HDCP-получателями глубина равна единице, а число устройств — четырём.

Число устройств в одном дереве не может превышать 127, а число уровней (глубина) — семи.

Пример:

HDCP-передатчик, определив, что передан бит REPEATER, устанавливает 5-секундный сторожевой таймер (watchdog) и запрашивает статус READY (готовность) у HDCP-повторителя. Если бит состояния установлен на 1 (готов), то HDCP-передатчик считывает список KSV и проверяет, не превышает ли список устройств установленный спецификацией объём и глубину, затем проверяет список на целостность, вычисляя V. Если какое-либо из условий не выполнено или истекает время таймера, то аутентификация не производится.

Повторная попытка осуществляется передачей нового значения An и Aksv.

Битовое представление состояния устройства B

Название поля	Занимаемые биты	Описание поля
Rsvd	15:14	Зарезервирован. Значение — 0.
HDMI_RESERVED_2	13	Зарезервирован.
HDMI_MODE	12	Режим HDMI. Когда бит установлен на единицу, HDCP-приёмник переходит из режима DVI в режим HDMI. Бит сбрасывается при включении устройства, его перезагрузке, подключении или отключении HDCP-передатчика или в том случае, когда HDCP-приёмник не получает данные в течение 30 кадров.
MAX_CASCADE_EXCEEDED	11	Отображает ошибки в топологии. Если установлен на единицу, то в дереве устройств находится более семи уровней повторителей.
DEPTH	10:8	Показывает число уровней в системе
MAX_DEVS_EXCEEDED	7	Отображает ошибки в топологии. Если установлен на единицу, то в дереве системы находится более 127 устройств.
DEVICE_COUNT	6:0	Полное число присоединенных устройств. Всегда равен нулю для HDCP-повторителей. Это число не включает сами HDCP-повторители, но устройства, к ним присоединенные.

Третья часть протокола аутентификации

Третья часть протокола работает в течение вертикального интервала (англ. vertical blanking interval), предшествующего кадру. Каждый из двух HDCP устройств вычисляет новые инициирующие числа Ki, Mi и Ri, где индекс i отображает номер кадра, начиная с единицы для первого кадра с шифрованием (после завершения первой части протокола аутентификации). Индекс увеличивается на единицу с каждым кадром или с каждым зашифрованным кадром в зависимости от того, включен ли режим ADVANCE_CIPHER. Счётчик кадров не увеличивается, если HDCP устройство находится в состоянии HDMI AVMUTE (режим, когда выключается звук, если происходят изменения, которые могут привести к шуму в аудиоканале), и не увеличивается после выхода из этого состояния до первого шифрованного кадра.

• Ki — 56-битный ключ, используемый для инициализации HDCP шифра, чтобы зашифровать или расшифровать HDCP контент.
• Mi — новая 64-битная инициирующая величина для HDCP шифра.
• Ri — 16-битное число, предназначенное для подтверждения целостности соединения (увеличивается каждые 128 кадров, начиная со 128).

HDCP-передатчик проверяет Ri’ по собственным вычислениям для того, чтобы подтвердить способность видеоприемника корректно расшифровывать информацию. Эта проверка делается как минимум каждые две секунды, также возможно синхронное чтение Ri во время очередного её изменения (каждые 128 кадров). При этом чтение Ri' должно завершиться в течение одной миллисекунды с того момента, как HDCP-передатчик инициирует это действие, если по каким-либо причинам операция не удалась, то HDCP-передатчик считает, что HDCP-приёмник не прошёл аутентификацию.

С целью увеличения вероятности обнаружения рассинхронизации в шифровании HDCP-передатчик и приёмник дополнительно могут поддерживать Enhanced Link Verification (усиленный контроль за соединением), в котором вычисления для поддержки контроля над синхронизацией шифра выполняются, если передается особый пиксель.

Режим ADVANCE_CIPHER — это дополнительный режим, в котором состояние шифра и счётчик кадров увеличиваются каждый кадр в режиме DVI или каждый кадр в режиме HDMI (если только он не находится в состоянии AVMUTE) вне зависимости от того, включено шифрование или нет.

Шифрование данных

HDCP-шифрование происходит на входе TMDS (англ. Transition Minimized Differential Signaling, дифференциальная передача сигналов с минимизацией перепадов уровней) шифратора, а расшифрование - на выходе TMDS-дешифратора. Процедура шифрования состоит из побитового сложения (XOR) потока данных с псевдослучайной последовательностью, генерируемой HDCP-шифром.

Блок-схема шифрования-расшифрования

Во время вертикального интервала функция hdcpBlockCipher подготавливает HDCP-шифр к генерации для каждого пикселя входного потока 24-битной псевдослучайной последовательности, зависящей от ключа. Эти биты накладываются на TMDS-каналы, как показано в таблице на примере RGB-видеопотока.

Отображение шифрованного потока

Выход шифра	Канал TMDS	Биты видеопотока
23:16	2	Red [7:0]
15:8	1	Green [7:0]
7:0	0	Blue [7:0]

Во время строчного интервала гашения (англ. horizontal-blanking interval) HDCP-шифр переназначает ключ каждые 56 бит, что усложняет задачу построчного взлома шифра.

HDCP-шифр

Структура HDCP шифра

Общую структуру HDCP-шифра можно разделить на три слоя. Первый слой состоит из четырёх линейных регистров сдвига с обратной связью (англ. linear feedback shift register, LFSR), на выходе которых получается один бит. Если подан сигнал повторного ввода ключа, то этот бит помещается в средний слой. Средний слой состоит из двух схожих частей. Первая часть — функция B раунда — выполняет один раунд блочного шифрования, используя три 28-битных регистра Bx, By, Bz. Вторая часть — функция K раунда — схожа по структуре с функцией B, но работает выходом защёлки Ky (поток 28-битных раундовых ключей к раундовой функции B с частотой один 28-битный ключ в один такт). В нижнем слое каждый такт происходит компрессия четырёх выходов 28-битных регистров By, Bz, Ky, Kz в 24-битный блок псевдослучайной последовательности.

Модуль линейных регистров сдвига с обратной связью

Модуль линейных регистров сдвига состоит из четырёх LFSR различной длины и разных смесителей (англ. combining function). Функция смешения зависит от трёх отводов (англ. tap) каждого регистра.

Пример одного из используемых регистров сдвига (LSFR0)

Полиномы регистров и используемые выводы

Номер регистра	Полином регистра	Выходы, используемые для функции смешения
		0	1	2
3	[math]\displaystyle{ x^{17} + x^{15} + x^{11} + x^{5} + 1 }[/math]	5	11	16
2	[math]\displaystyle{ x^{16} + x^{15} + x^{12} + x^{8} + x^{7} + x^{5} + 1 }[/math]	5	9	15
1	[math]\displaystyle{ x^{14} + x^{11} + x^{10} + x^{7} + x^{6} + x^{4} + 1 }[/math]	4	8	13
0	[math]\displaystyle{ x^{13} + x^{11} + x^{9} + x^{5} + 1 }[/math]	3	7	12

Функция смешения состоит из четырёх каскадно-соединенных сетей с перемещением каналов (англ. shuffle network), каждая из которых включает в себя два бита состояния. Над одними отводами каждого из четырёх регистров производится операция XOR для того, чтобы сформировать входные данные для первого каскада сети. Другие отводы регистров используются для выбора входа в одну из сетей. Выход четвёртой сети складывается (XOR) с одним отводом от каждого регистра.

Устройство функции смешения)

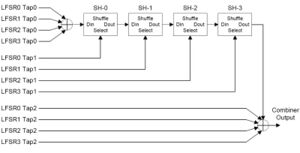
Сеть с перемещением каналов

На рисунке схематически изображена сеть с перемещением каналов. В том случае, если в сети содержится пара булевских значений (A, B), на вход поступает булевская величина D, а вход выбора S, то значение параметра S определяет следующее состояние. Если S — ноль, то на выход поступает A и устанавливается состояние (B, D). Если S — единица, то на выходе - B и устанавливается состояние (A, D).

Устройство сети с перемещением каналов

Во всех режимах работы LSFR и функция смешения инициализируются 56-битным числом. 60 битов LSFR-состояния используют эти 56 битов непосредственно, плюс дополнение некоторых четырёх бит. Shuffle-сети инициализируются той же величиной.

Однобитовый выходной поток функции смешения — это единственные данные, получаемые из работы модуля LSFR. Этот поток снабжает модуль блоков материалом для создания ключей, если поступил сигнал на переопределение ключа.

Инициализация регистров сдвига

	Бит	Начальное значение
LFSR3	[16]	Дополнение ко входному биту [47]
	[15:0]	Входные биты [55:40]
LFSR2	[15]	Дополнение ко входному биту [32]
	[14:0]	Входные биты [39:25]
LFSR1	[13]	Дополнение ко входному биту [18]
	[12:0]	Входные биты [24:12]
LFSR0	[12]	Дополнение ко входному биту [6]
	[11:0]	Входные биты [11:0]
Shuffle networks	Регистр A	0
	Регистр В	1

Модуль блоков

Устройство раундовых функций

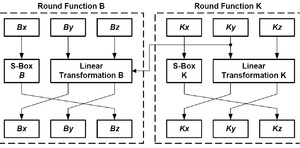
Этот модуль состоит из двух отдельных компонент, называемых раундовыми функциями. Одна из компонент - раундовая функция K снабжает другую компоненту — раундовую функцию B — потоком ключей. Каждая компонента работает с соответствующим набором трёх 28-битных регистров.

Если поступил сигнал на переопределение ключа, то в тринадцатый бит регистра Ky записывается бит из выходного потока модуля LSFR.

S-блоки для обеих раундовых функций состоят из семи S-блоков с четырьмя входами и четырьмя выходами. Для раундовой функции K S-блоки названы SK0, SK1.. ,SK6. Для раундовой функции B S-блоки названы SB0, SB1.., SB6. В I-й вход блока J записывается бит под номером I*7+J регистров Bx или Kx, а на выход I блока J подается бит I*7+J регистров Bz, Kz. При этом бит ноль считается младшим разрядом.

Таблица для логической функции диффузионной сети

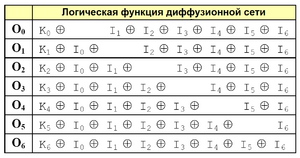
Диффузионные сети для раундовой функции К показаны в таблице. Следует заметить, что ни в одной диффузионной сети для этой функции нет дополнительных входов. В половине диффузионных компонент функции B присутствуют дополнительные входы, в которые поступают биты из регистра Ky раундовой функции K.

Диффузия раундовой функции K

Диффузия раундовой функции B (прочерк означает, что у данной компоненты нет дополнительного входа)

Логическая функция выхода

Регистры Ky, Kz, By, Bz образуют логическую функцию выхода. Каждый из 24 битов получается путём сложения (XOR) девяти членов, как показывает формула ниже:

[math]\displaystyle{ (B0*K0) \oplus_2(B1*K1) \oplus_2(B2*K2) \oplus_2(B3*K3) \oplus_2(B4*K4) \oplus_2(B5*K5) \oplus_2 (B6*K6) \oplus_2 B7 \oplus_2 K7 }[/math]
Где [math]\displaystyle{ \oplus_2 }[/math] — XOR, a [math]\displaystyle{ * }[/math] — логическое умножение

Отображение входов и выходов логической функции выхода

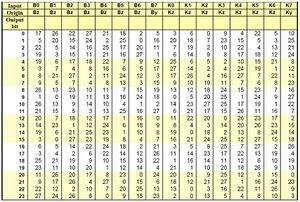
Пример: Выходной бит 0 вычисляется следующим образом: [math]\displaystyle{ (Bz17*Kz3) \oplus_2 (Bz26*Kz6) \oplus_2 (Bz22*Kz0) \oplus_2 }[/math]
[math]\displaystyle{ \oplus_2 (Bz27*Kz9) \oplus_2 (Bz21*Kz4) \oplus_2 (Bz18*Kz22) \oplus_2 }[/math]
[math]\displaystyle{ \oplus_2 (Bz2*Kz5) \oplus_2 By5 \oplus_2 Ky10 }[/math]

Некоторые используемые функции

hdcpBlockCipher

Эта последовательность используется во время первой части протокола аутентификации, чтобы выработать сессионный ключ Ks и во время вертикального интервала, предшествующего шифрованному кадру, чтобы получить ключ кадра Ki.

Последовательность работы функции hdcpBlockCipher

Начальные состояния и выход функции hdcpBlockCipher\

Этап Действие 1 Загрузка регистров B и K модуля блоков 2 Совершение 48 тактов работы регистров 3 Сохранение 56 младших битов для будущего использования в качестве Ks, Ki 4 Перенос 84 битов регистров B в регистры K 5 Перезагрузка регистра B 6 Инициализация модуля LFSR 7 Запрос на смену ключа 8 Совершение 56 тактов работы LFSR и модуля блоков, сохранение 64-битного значения Mi во время последних четырёх тактов 9 Снятие запроса на смену ключа

Этап Такты Начальное значение LFSR (56 бит) Начальное значение K Начальное значение B (65 бит) Выход B (84 бита) Выход функции hdcpBlockCipher во время аутентификации 1-3 48 — Km (56 бит) REPEATER||An Ks — 6-9 56 Ks Ks (84 бит) REPEATER ||An — [math]\displaystyle{ R0, M0 }[/math] hdcpBlockCipher во время вертикального интервала 1-3 48 — Ks (56 бит) REPEATER ||[math]\displaystyle{ M_{i-1} }[/math] [math]\displaystyle{ K_i }[/math] — 6-9 56 [math]\displaystyle{ Ki }[/math] [math]\displaystyle{ Ki }[/math] (84 бит) REPEATER ||[math]\displaystyle{ M_{i-1} }[/math] — [math]\displaystyle{ R_i, M_i }[/math]

Для 8-битных чисел a и b результатом конкатенации ab является 16-битное число, где a — старший разряд, а b — младший разряд.

В обеих раундовых функциях B и K регистры x, y, z можно рассматривать как один регистр длиной в 84 бита.

В том случае, когда требуется менее 84 битов регистра, используются биты младшего разряда. Если для инициализации доступно менее 84 бит, то заполняются младшие биты, а оставшиеся устанавливаются в ноль.

Пример:
65-битный результат конкатенации бита REPEATER и величины An будет записан в регистры Bx и By, 
плюс в 9 младших бит регистра Bz,  при этом старшие 19 бит регистра заполнятся нулями.
Откуда берутся биты Mi и Ri, показано в таблице выше.

hdcpRngCipher

Эта функция используется как генератор случайных чисел, причём функция должна поддерживать метод, который позволял бы получать биты из внешнего источника. Должно происходить смешивание битов извне со значениями регистров (без замены). То есть не должно существовать способа определить генерируемую величину.

Внешний источник должен обладать разумной вероятностью, или энтропией. То есть, если, например, дан 1000000 различных циклов, то количество повторяющихся чисел среди 1000000 An не должно превышать 50 %. Это соответствует примерно сорока (если считать, что [math]\displaystyle{ 1000000 \approx 2^{20} }[/math]) произвольным битам из 64.

Криптоанализ

Для того, чтобы получить общий секрет, устройства складывают свои секретные ключи Ai в зависимости от полученного вектора ключа. В итоге получается 56-битный секрет Km (передатчик) и Km’ (приёмник), причём они должны быть равны.

Затем, после аутентификации приёмник шифрует оказию полученным ключом и отправляет её передатчику. Тот, в свою очередь, проверяет своим ключом Km, что оказия зашифрована верно.

Следовательно, если мы определим 40 линейно независимых векторов [math]\displaystyle{ A_1.. A_{40} }[/math] (секретные ключи устройства), то мы сможем полностью взломать систему, поскольку эти ключи будут составлять базис 40-мерного пространства секретных ключей, и мы сможем составить из них любой набор секретных ключей любого устройства. С другой стороны, если не все 40 ключей будут линейно независимыми, то мы все равно сможем создать определенные наборы секретных ключей, входящих в найденное подпространство.

Пример:
Предположим, что у нас есть 40 устройств [math]\displaystyle{ ( A_1 \dots A_{40} ) }[/math], для которых мне известны их векторы выбора ключей и 
наборы секретных ключей   [math]\displaystyle{ ((A_1)keys \dots(A_{40})keys) }[/math], тогда, в результате обмена информацией с устройством, 
которое мы хотим взломать, получится система уравнений:
[math]\displaystyle{ 
  \begin{cases}
       Xkeys  * (A_1)ksv = (A_1)keys  * Xksv \\
       Xkeys  * (A_2)ksv = (A_2)keys  * Xksv \\
       \dots\\
       Xkeys * (A_{40})ksv = (A_{40})keys * Xksv \\
  \end{cases}
   }[/math]

решив которую, мы получим секретные ключи атакуемого устройства. Предположение, которое мы делаем — то, что все 40 векторов выбора ключа [math]\displaystyle{ (Ai) }[/math]ksv линейно независимы.

Если же пространство, охватываемое [math]\displaystyle{ (Ai)ksv }[/math] не является 40-мерным, то всё равно должна остаться лазейка. Или эти векторы выбора ключа сконструированы так, что будет невозможно составить из них базис сорокамерного пространства, или нам потребуется более 40 KSV, чтобы охватить всё пространство (каждое дополнительное устройство обладает малыми шансами быть линейно зависимым к уже полученному набору, примерно [math]\displaystyle{ \frac {1}{2^{40 - n}} }[/math], где n — размерность охваченного пространства)

Мы также можем сами создать правильные наборы вектора выбора ключа и секретных ключей устройства из линейной комбинации уже нам известных.

Пример:

1. Выберем произвольное устройство B, если B может аутентифицировать Ai, то выполняется равенство:

[math]\displaystyle{ (K_i)m' = (A_1)keys * Bksv = Bkeys * (A_i)ksv = (K_i)m. }[/math]

2. Пусть

[math]\displaystyle{ Xksv = a_1 * (A_1)ksv + a_2 * (A_2)ksv ... a_n * (A_n)ksv. }[/math]

3. Мы знаем, что, когда устройство B аутентифицирует устройство X, используется величина Km:

[math]\displaystyle{ Km = Bkeys * Xksv = Bkeys * (a_1 * (A_1)ksv + a_2 * (A_2)ksv + ... + a_n (A_n)ksv) = a_1 * (A_1)ksv * Bkeys + ... + a_n * (A_n)ksv * Bkeys = a_1 * (K_1)m + a+2 * (K_2)m + ... + a_n (K_n)m. }[/math]

4. То есть, вспоминая тот факт, что (Ki)'m = Ki для всех i, мы можем вычислить Km':

[math]\displaystyle{ Km' = a_1 * (K_1)m' + a_2 * (K_2)m' + ... + a_n * (K_n)m' = a_1 * (A_1)keys * Bksv + ... + a_n * (A_n)keys * Bksv = [ a_1 * (A_1)keys + ... + a_n * (A_n)keys ] * Bksv. }[/math]

5. Так как выбор B был произвольным, то это сработает для любого B, причём

[math]\displaystyle{ Xkeys = a_1 * (A_1)keys + ... + a_n * (A_n)keys. }[/math]

Аутентификация между B и X пройдет успешно. Единственной сложностью может быть конструирование Xksv таким образом, чтобы он состоял из 20 нулей и 20 единиц.

Применение HDCP

Используется в HD DVD и Blu-ray плеерах. Если устройство воспроизведения и, в случае использования компьютера, ПО не поддерживают HDCP, то сигнал не будет транслироваться на выход, либо будет, но c деградированым качеством (англ. Image Constraint Token flag).

Одобрена 4 августа 2004 г. Федеральным агентством по связи США (англ. Federal Communications Commission, FCC) как "Технология защиты цифровых выходов (англ. Digital Output Protection Technology).

Технология поддерживается ОС Windows Vista.

Поддержка HDCP является обязательным условием соответствия марке «HD ready», также его применение насаждается законами США для всех приёмников вещания высокой чёткости.

См. также

• AACS
• HDTV

Ссылки

• Digital Content Protection LLC organization (англ.) (недоступная ссылка). — Официальный сайт организации, лицензирующей технологию. Архивировано 25 февраля 2012 года.
• Digital Content Protection LLC. HDCP specification v1.4 (англ.) (недоступная ссылка). — Спецификация технологии HDCP. Архивировано 25 февраля 2012 года.
• Scott A. Crosby. Apparent HDCP authentication protocol weaknesses (англ.) (недоступная ссылка). — Уязвимости протокола аутентификации HDCP. Архивировано 25 февраля 2012 года.
• Keith Irwin. Four Simple Cryptographic Attacks on HDCP (англ.) (недоступная ссылка). — Четыре простых атаки на HDCP. Архивировано 25 февраля 2012 года.
• Scott Crosby, Ian Goldberg, Robert Johnson, Dawn Song, David Wagner. A Cryptanalysis of the HDCP (англ.) (недоступная ссылка). — Детальный криптоанализ HDCP. Архивировано 25 февраля 2012 года.