Эффект Нернста — Эттингсгаузена
Эффект Нернста — Эттингсгаузена, или поперечный эффект Нернста — Эттингсгаузена, — термомагнитный эффект, наблюдаемый при помещении полупроводника, в котором имеется градиент температуры, в магнитное поле. Данный эффект был открыт в 1886 году В. Нернстом и А. Эттингсгаузеном. В 1948 году эффект в металлах получил своё теоретическое обоснование в работе Зондхаймера[1]
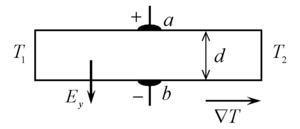
Суть эффекта состоит в том, что в полупроводнике появляется электрическое поле [math]\displaystyle{ \mathbf{E} }[/math], перпендикулярное к вектору градиента температур [math]\displaystyle{ \nabla T }[/math] и вектору магнитной индукции [math]\displaystyle{ \mathbf{B} }[/math], то есть в направлении вектора [math]\displaystyle{ [\nabla T,\;\mathbf{B}] }[/math]. Если градиент температуры направлен вдоль оси [math]\displaystyle{ X }[/math], а магнитная индукция — вдоль [math]\displaystyle{ Z }[/math], то электрическое поле параллельно вдоль оси [math]\displaystyle{ Y }[/math]. Поэтому между точками [math]\displaystyle{ a }[/math] и [math]\displaystyle{ b }[/math] (см. рис.) возникает разность электрических потенциалов [math]\displaystyle{ u }[/math]. Величину напряжённости электрического поля [math]\displaystyle{ E_y }[/math] можно выразить формулой:
- [math]\displaystyle{ E_y=\frac{u}{d}=q_\bot B_z\frac{dT}{dx}, }[/math]
где [math]\displaystyle{ q_\bot }[/math] — так называемая постоянная Нернста — Эттингсгаузена, которая зависит от свойств полупроводника и может принимать как положительные, так и отрицательные значения. Например, в германии с удельным сопротивлением ~ 1 Ом/см при комнатной температуре, при [math]\displaystyle{ B\sim 10^3 }[/math] Гс и [math]\displaystyle{ dT/dx\sim 10^2 }[/math] К/см наблюдается электрическое поле [math]\displaystyle{ E_y\sim 10^{-2} }[/math] В/см. Значение постоянной [math]\displaystyle{ q_\bot }[/math], а следовательно и [math]\displaystyle{ E_y }[/math], сильно зависят от температуры образца и от магнитного поля и при изменении этих величин могут даже изменять знак.
Поперечный эффект Нернста — Эттингсгаузена возникает по той же причине, что и эффект Холла, то есть в результате отклонения потока заряженных частиц силой Лоренца. Различие, однако, заключается в том, что при эффекте Холла направленный поток частиц возникает в результате их дрейфа в электрическом поле, а в данном случае — в результате диффузии.
Существенным отличием является также тот факт, что, в отличие от постоянной Холла, знак [math]\displaystyle{ q_\bot }[/math] не зависит от знака носителей заряда. Действительно, при дрейфе в электрическом поле изменение знака заряда приводит к изменению направления дрейфа, что и даёт изменение знака поля Холла. В данном же случае поток диффузии всегда направлен от нагретого конца образца к холодному, независимо от знака заряда частиц. Поэтому направления силы Лоренца для положительных и отрицательных частиц взаимно противоположны, однако направление потоков электрического заряда в обоих случаях одно и то же.
Продольный эффект Нернста — Эттингсгаузена
Продольный эффект Нернста — Эттингсгаузена заключается в изменении термоэдс металлов и полупроводников под влиянием магнитного поля.
В отсутствие магнитного поля термоэдс в электронном полупроводнике определяется разностью компонент скоростей быстрых электронов (движущихся с горячей стороны) и медленных электронов (движущихся с холодной стороны) вдоль градиента температуры.
При наличии магнитного поля продольные (вдоль градиента температуры) и поперечные (поперек градиента температуры) компоненты скоростей электронов изменяются в зависимости от угла поворота скорости электронов в магнитном поле, определяемого временем свободного пробега электронов [math]\displaystyle{ \tau }[/math] в металле или полупроводнике.
Если время свободного пробега [math]\displaystyle{ \tau }[/math] для медленных электронов или дырок (в полупроводниках) больше, чем для быстрых, то [math]\displaystyle{ \frac{v_{1x}(H)}{v_{1x}(0)}\gt \frac{v_{2x}(H)}{v_{2x}(0)} }[/math], где [math]\displaystyle{ v_{1x}(H),\;v_{2x}(H) }[/math] — продольные компоненты скоростей медленных и быстрых электронов при наличии магнитного поля, [math]\displaystyle{ v_{1x}(0),\;v_{2x}(0) }[/math] — продольные компоненты скоростей медленных и быстрых электронов при отсутствии магнитного поля. Величина термоэдс в магнитном поле, пропорциональная разности [math]\displaystyle{ v_{2x}(H)-v_{1x}(H) }[/math] будет больше, чем в отсутствие магнитного поля при разности [math]\displaystyle{ v_{2x}(0)-v_{1x}(0) }[/math]. И, наоборот, если время свободного пробега [math]\displaystyle{ \tau }[/math] для медленных электронов меньше, чем для быстрых, наличие магнитного поля уменьшает термоэдс.
В электронных полупроводниках термоэдс в магнитном поле увеличивается, если время свободного пробега [math]\displaystyle{ \tau }[/math] уменьшается с увеличением энергии электрона (при рассеянии на акустических фононах).
В электронных полупроводниках термоэдс в магнитном поле уменьшается, если время свободного пробега [math]\displaystyle{ \tau }[/math] увеличивается с увеличением энергии электрона (при рассеянии на ионизированных атомах примеси).[2]
Литература
- Блатт Ф. Дж. Теория подвижности электронов в твёрдых телах / Пер. с англ. — М.: Физматлит, 1963. — 224 с.
- Цидильковский И. М. Термомагнитные явления в полупроводниках. — М.: Физматгиз, 1960. — (Серия «Физика полупроводников и полупроводниковых приборов»). — 396 с.
- Житинская М. К., Немов С. А., Свечникова Т. Е. Влияние неоднородностей кристаллов Bi2Te3 на поперечный эффект Нернста — Эттингсгаузена // Физика и техника полупроводников. — 1997. — Т. 31. — № 4. — с. 441—443.
Примечания
- ↑ Sondheimer E. H. The Theory of the Galvanomagnetic and Thermomagnetic Effects in Metals // Proceedings of the Royal Society A. — July 21, 1948. — №193. — pp. 484-512; doi:10.1098/rspa.1948.0058.
- ↑ Аскеров Б. М. Кинетические эффекты в полупроводниках. — Л.: Наука, 1970.