Производственная функция Кобба-Дугласа

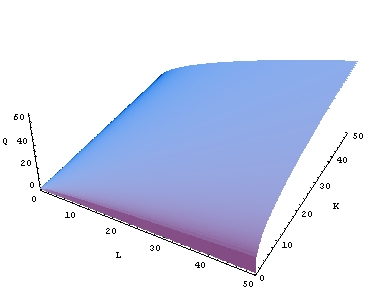
Производственная функция Кобба — Дугласа (англ. Cobb–Douglas production function) — производственная функция (или функция полезности), отражающая зависимость объёма производства [math]\displaystyle{ Q }[/math] от создающих его факторов производства — затрат труда [math]\displaystyle{ L }[/math] и капитала [math]\displaystyle{ K }[/math].

История создания

Впервые была предложена Кнутом Викселлем. В 1928 году функция проверена на статистических данных Чарльзом Коббом и Полом Дугласом в работе «Теория производства». В этой статье была предпринята попытка эмпирическим путём определить влияние затрачиваемого капитала и труда на объём выпускаемой продукции в обрабатывающей промышленности США.

Определение

Общий вид функции:

[math]\displaystyle{ Q = A \times L^{\alpha} \times K^{\beta} }[/math],

где [math]\displaystyle{ A }[/math] — технологический коэффициент, [math]\displaystyle{ \alpha \geqslant 0 }[/math] — коэффициент эластичности по труду, а [math]\displaystyle{ \beta \geqslant 0 }[/math] — коэффициент эластичности по капиталу.

Если сумма показателей степени ([math]\displaystyle{ \alpha + \beta }[/math]) равна единице, то функция Кобба — Дугласа является линейно однородной, то есть она демонстрирует постоянную отдачу при изменении масштабов производства.

Если сумма показателей степени больше единицы, функция отражает возрастающую отдачу, а если она меньше единицы, — убывающую. Изокванта, соответствующая функции Кобба — Дугласа, будет выпуклой и «гладкой».

Впервые производственная функция была рассчитана в 1920-е годы для обрабатывающей промышленности США, в виде равенства:

[math]\displaystyle{ Q \sim L^{0.73} \times K^{0.27} }[/math].

Обобщением функции Кобба — Дугласа является функция с постоянной эластичностью замещения факторов (CES-функция): [math]\displaystyle{ Q = A[ \alpha L^{-\rho} + \beta K^{-\rho} ]^{-\frac{1}{\rho}} }[/math], для которой в пределе при [math]\displaystyle{ \rho \rightarrow 0 }[/math] получаем [math]\displaystyle{ Q = A \times L^{\alpha} \times K^{\beta} }[/math].

Разногласия

Ни Кобб, ни Дуглас не предоставили теоретических обоснований постоянства коэффициента [math]\displaystyle{ \lambda }[/math] в разных секторах экономики. Например, рассмотрев функции для двух секторов экономики с одинаковыми технологическими коэффициентами:

[math]\displaystyle{ Q_{1}=A\times L_{1}^{\lambda}\times K_{1}^{1-\lambda} }[/math],

[math]\displaystyle{ Q_{2}=A\times L_{2}^{\lambda}\times K_{2}^{1-\lambda} }[/math],

в сумме не будет получаться ожидаемое:

[math]\displaystyle{ Q_{1} + Q_{2}=A\times (L_{1}+L_{2})^{\lambda}\times (K_{1}+K_{2})^{1-\lambda} }[/math].

Равенство возможно лишь если:

[math]\displaystyle{ \frac{L_{1}}{L_{2}} = \frac{K_{1}}{K_{2}} }[/math].

См. также

Литература

Renshaw, Geoff. Maths for Economics (англ.). — New York: Oxford University Press, 2005. — P. 516—526. — ISBN 0-19-926746-4.