Сферическое зеркало

Мнимое изображение фотокамеры и окружающего пространства в выпуклом сферическом зеркале — ёлочном шаре.

Сферическое зеркало — зеркало, отражающая поверхность которого имеет вид сегмента сферы.

Описание

Сферическое зеркало может быть выпуклым или вогнутым — в зависимости от того, какая сторона сегмента сферы — выпуклая или вогнутая — является отражающей. Центр соответствующей сферическому зеркалу сферы называется его центром или оптическим центром, середина сегмента — полюсом зеркала, прямая, проходящая через центр и полюс — главной оптической осью зеркала. Другие прямые, проходящие через центр зеркала и точку, отличную от полюса, называются его побочными оптическими осями.

Параксиальные лучи, параллельные главной оптической оси выпуклого сферического зеркала, так же как и продолжения параксиальных лучей, параллельных главной оптической оси вогнутого сферического зеркала, пересекаются в одной точке, называемой его фокусом. Он расположен посередине между центром и полюсом зеркала, то есть расстояние (f) его до зеркала равно половине радиуса (R):

[math]\displaystyle{ f=\frac{R}{2} }[/math]

У сферического зеркала, как вообще у любого зеркала, отсутствует хроматическая аберрация, но выражена сферическая аберрация. Сферическая аберрация выражена потому, что в отличие от параболического зеркала (то есть сегмента параболоида вращения), сферическое зеркало может собирать в одной точке лишь параксиальные лучи, то есть те из лучей, параллельных главной оптической оси, которые близки к этой оси. Сферическая аберрация в одном из примеров применения сферического вогнутого зеркала, зеркально-линзовом телескопе системы Дмитрия Максутова, устраняется компенсированием специально подобранной линзой — мениском.

Известным примером выпуклого сферического зеркала является ёлочный шар.

Построение изображения в сферическом зеркале

Проще всего построить изображение отрезка, перпендикулярного главной оптической оси зеркала и настолько небольшого по высоте, что луч, исходящий из его верхней точки и параллельный главной оптической оси зеркала — параксиальный. Его изображение будет также перпендикулярным главной оптической оси зеркала, расстояние его от зеркала при известном расстоянии от зеркала до предмета и фокусного расстояния зеркала можно вычислить по формуле зеркала. Высота изображения (y') будет равна произведению высоты предмета (y) на отношение расстояния от изображения до зеркала (v) к расстоянию от зеркала до предмета (u):

[math]\displaystyle{ y'=y\cdot\frac{v}{u} }[/math]

Для вогнутого сферического зеркала

Видеоурок: вогнутое зеркало

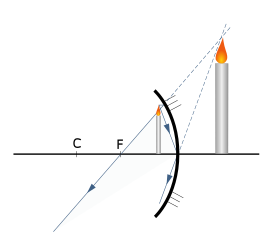
Если сферическое зеркало вогнутое, возможны различные случаи расположения изображения относительно зеркала при различных расстояниях до предмета. Буквой C обозначен центр зеркала, а буквой F — его фокус. При u>f формула зеркала имеет вид:

[math]\displaystyle{ \frac{1}{u}+\frac{1}{v}=\frac{2}{R}, }[/math]

а при u<f:

[math]\displaystyle{ \frac{1}{u}-\frac{1}{v}=\frac{2}{R}. }[/math]

Для построения взято три луча (хотя достаточно и двух):

• луч, параллельный главной оптической оси после отражения от зеркала пройдёт через его фокус;
• луч, проходящий через фокус после отражения пойдёт параллельно главной оптической оси;
• луч, падающий на полюс зеркала после отражения пойдёт под углом, равным углу падения (по закону отражения света).

Если предмет приближён к зеркалу и находится на расстоянии, превышающем расстояние от зеркала до его центра, то изображение его будет действительным, перевёрнутым и уменьшенным и расположится на отрезке между центром и фокусом.

Если предмет помещён в центре зеркала, то его изображение также будет расположено в центре зеркала. Изображение получается действительным, перевёрнутым и равным по величине предмету.

Если предмет помещён между центром и фокусом, то изображение будет расположено дальше от зеркала, чем его центр и будет действительным, перевёрнутым и увеличенным.

Если предмет ближе фокуса к зеркалу, то изображение — мнимое, прямое, увеличенное, по другую сторону зеркала от предмета.

Для выпуклого сферического зеркала

Построение изображения в выпуклом сферическом зеркале проще, чем в вогнутом: здесь при любом расстоянии предмета до зеркала его изображение будет расположено за зеркалом. На рисунке ниже буквой F обозначен фокус выпуклого зеркала, буквой V — полюс, y (в формуле u) — высота предмета, y' (в формуле v) — высота изображения. Формула зеркала в этом случае имеет вид:

[math]\displaystyle{ \frac{1}{u}-\frac{1}{v}=-\frac{2}{R} }[/math]

Для построения взято два луча:

• луч от верхней точки предмета, параллельный главной оптической оси, отразится от зеркала, и продолжение этого отражённого луча пройдёт через фокус и через верхнюю точку изображения;
• луч от верхней точки предмета, продолжение которого проходит через фокус, после отражения пойдёт параллельно главной оптической оси, а продолжение этого отражённого луча также пройдёт через верхнюю точку изображения.

Таким образом, верхней точкой изображения будет точка пересечения продолжения первого отражённого луча и продолжения второго отражённого луча.

Изображение в выпуклом зеркале — мнимое, прямое, уменьшенное, находится по другую сторону зеркала от предмета.

См. также

• Линза
• Геометрическая оптика

Литература

• Ландсберг Г.С. Элементарный учебник физики. — 13-е изд. — М.: Физматлит, 2003. — Т. 3. Колебания и волны. Оптика. Атомная и ядерная физика. — С. 249—266. — 656 с. — ISBN 5922103512.
• Ландсберг Г. С. Оптика: учебное пособие для вузов. — 6-е изд. стереот. — М.: ФИЗМАТЛИТ, 2003. — 848 с. — ISBN 5-9221-0314-8.
• Делоне Н. Б. Статья «Нелинейная оптика», 1997, Физика
• Родионов С. А. Глава 4. Основные законы геометрической оптики. // Основы оптики. Конспект лекций. — СПб.: СПб ГИТМО (ТУ), 2000. — 167 с.