Пузырьковая сортировка

Пузырьковая сортировка, сортиро́вка простыми обменами (англ. bubble sort) — простой алгоритм сортировки. Для понимания и реализации этот алгоритм — простейший, но эффективен он лишь для небольших массивов. Сложность алгоритма: [math]\displaystyle{ O }[/math][math]\displaystyle{ (n^2) }[/math].

Алгоритм считается учебным и практически не применяется вне учебной литературы, вместо него на практике применяются более эффективные алгоритмы сортировки. В то же время метод сортировки обменами лежит в основе некоторых более совершенных алгоритмов, таких как шейкерная сортировка, пирамидальная сортировка и быстрая сортировка.

Алгоритм

Алгоритм состоит из повторяющихся проходов по сортируемому массиву. За каждый проход элементы последовательно сравниваются попарно и, если порядок в паре неверный, выполняется перестановка элементов. Проходы по массиву повторяются [math]\displaystyle{ N-1 }[/math] раз или до тех пор, пока на очередном проходе не окажется, что обмены больше не нужны, что означает — массив отсортирован. При каждом проходе алгоритма по внутреннему циклу очередной наибольший элемент массива ставится на своё место в конце массива рядом с предыдущим «наибольшим элементом», а наименьший элемент перемещается на одну позицию к началу массива («всплывает» до нужной позиции, как пузырёк в воде — отсюда и название алгоритма).

Реализация

Сложность: [math]\displaystyle{ O(n^2) }[/math].

Наихудший случай:

• Число сравнений в теле цикла равно [math]\displaystyle{ (N-1) \frac N 2 }[/math].
• Число сравнений в заголовках циклов равно [math]\displaystyle{ (N-1) \frac N 2 }[/math].
• Суммарное число сравнений равно [math]\displaystyle{ (N-1)N }[/math].
• Число присваиваний в заголовках циклов равно [math]\displaystyle{ (N-1) \frac N 2 }[/math].
• Число обменов равно [math]\displaystyle{ (N-1) \frac N 2 }[/math], что в [math]\displaystyle{ \frac N 2 }[/math] раз больше, чем в сортировке выбором.

Наилучший случай (на вход подаётся уже отсортированный массив):

• Число сравнений в теле цикла равно [math]\displaystyle{ (N-1) \frac N 2 }[/math].
• Число сравнений в заголовках циклов равно [math]\displaystyle{ (N-1) \frac N 2 }[/math].
• Суммарное число сравнений равно [math]\displaystyle{ (N-1)N }[/math].
• Число обменов равно [math]\displaystyle{ 0 }[/math].

Особенность данного алгоритма заключается в следующем: после первого завершения внутреннего цикла максимальный элемент массива всегда находится на [math]\displaystyle{ N }[/math]-ой позиции. При втором проходе, следующий по значению максимальный элемент находится на [math]\displaystyle{ N-1 }[/math] месте. И так далее. Таким образом, на каждом следующем проходе число обрабатываемых элементов уменьшается на 1 и нет необходимости «обходить» весь массив от начала до конца каждый раз.

Так как подмассив из одного элемента не нуждается в сортировке, то для сортировки требуется делать не более [math]\displaystyle{ N-1 }[/math] итераций внешнего цикла. Поэтому в некоторых реализациях внешний цикл всегда выполняется ровно [math]\displaystyle{ N-1 }[/math] и не отслеживается, были или не были обмены на каждой итерации.

Введение индикатора (флажка F) действительно произошедших во внутреннем цикле обменов уменьшает число лишних проходов в случаях с частично отсортированными массивами на входе. Перед каждым проходом по внутреннему циклу флажок сбрасывается в 0, а после действительно произошедшего обмена устанавливается в 1. Если после выхода из внутреннего цикла флажок равен 0, то обменов не было, то есть массив отсортирован и можно досрочно выйти из программы сортировки.

Псевдокод ещё более улучшенного алгоритма с проверкой действительно произошедших обменов во внутреннем цикле.

На входе: массив [math]\displaystyle{ A[N] }[/math], состоящий из [math]\displaystyle{ N }[/math] элементов, с нумерацией от [math]\displaystyle{ A[0] }[/math] до [math]\displaystyle{ A[N-1] }[/math]

 ЦИКЛ ДЛЯ J=1 ДО N-1 ШАГ 1                       FOR J=1 TO N-1 STEP 1
   F=0                                             F=0
   ЦИКЛ ДЛЯ I=0 ДО N-1-J ШАГ 1                     FOR I=0 TO N-1-J STEP 1
     ЕСЛИ A[I] > A[I+1] ТО ОБМЕН A[I],A[I+1]:F=1     IF A[I]>A[I+1] THEN SWAP A[I],A[I+1]:F=1
   СЛЕДУЮЩЕЕ I                                     NEXT I
   ЕСЛИ F=0 ТО ВЫХОД ИЗ ЦИКЛА                      IF F=0 THEN EXIT FOR
 СЛЕДУЮЩЕЕ J                                     NEXT J

В случае досрочного выхода из сортировки в этом алгоритме делается один избыточный проход без обменов.

Наихудший случай (не улучшается):

• Число сравнений в теле цикла равно [math]\displaystyle{ (N-1) \frac N 2 }[/math].
• Число сравнений в заголовках циклов [math]\displaystyle{ (N-1) \frac N 2 }[/math].
• Суммарное число сравнений равно [math]\displaystyle{ (N-1)N }[/math].
• Число присваиваний в заголовках циклов равно [math]\displaystyle{ (N-1) \frac N 2 }[/math].
• Число обменов равно [math]\displaystyle{ (N-1) \frac N 2 }[/math].

Наилучший случай (улучшается):

• Число сравнений в теле цикла равно [math]\displaystyle{ (N-1) }[/math].
• Число сравнений в заголовках циклов [math]\displaystyle{ (N-1) }[/math].
• Суммарное число сравнений равно [math]\displaystyle{ 2(N-1) }[/math].
• Число обменов равно [math]\displaystyle{ 0 }[/math].

Время сортировки 10000 коротких целых чисел на одном и том же программно-аппаратном комплексе (операция сравнения ≈3.4мкс, обмена ≈2.3мкс) сортировкой выбором составило ≈40сек., ещё более улучшенной сортировкой пузырьком ≈30сек, а быстрой сортировкой ≈0,027сек.

[math]\displaystyle{ O(n \cdot n) }[/math] больше, чем [math]\displaystyle{ O(n \cdot \log n) }[/math] у сортировки слиянием, но при малых [math]\displaystyle{ n }[/math] разница не очень большая, а программный код очень прост, поэтому вполне допустимо применение сортировки пузырьком для множества задач с массивами малой размерности на простаивающих и малозагруженных машинах.

Алгоритм можно немного улучшить, сделав следующее:

• Внутренний цикл можно модифицировать так, чтобы он поочерёдно просматривал массив то с начала, то с конца. Модифицированный таким образом алгоритм называется сортировкой перемешиванием или шейкерной сортировкой. Сложность при этом [math]\displaystyle{ O(n \cdot n) }[/math] не уменьшается.

В сортировке пузырьком, при каждом проходе по внутреннему циклу, можно добавить определение очередного минимального элемента и помещение его в начало массива, то есть объединить алгоритмы сортировки пузырьком и сортировки выбором, при этом число проходов по внутреннему циклу сокращается вдвое, но более чем вдвое увеличивается число сравнений и добавляется один обмен после каждого прохода по внутреннему циклу.

Псевдокод объединённого алгоритма сортировки пузырьком и сортировки выбором (устойчивая реализация):

 FOR J=0 TO N-1 STEP 1
   F=0
   MIN=J
   FOR I=J TO N-1-J STEP 1 
     IF Y[I]>Y[I+1] THEN SWAP Y[I],Y[I+1]:F=1
     IF Y[I]<Y[MIN] THEN MIN=I
   NEXT I
   IF F=0 THEN EXIT FOR
   IF MIN<>J THEN SWAP Y[J],Y[MIN]
 NEXT J

C

Пример работы алгоритма

Возьмём массив с числами «5 1 4 2 8» и отсортируем значения по возрастанию, используя сортировку пузырьком. Выделены те элементы, которые сравниваются на данном этапе.

Наглядная демонстрация алгоритма.

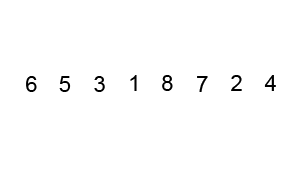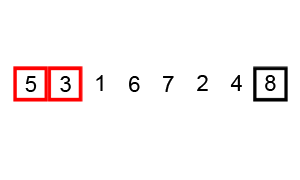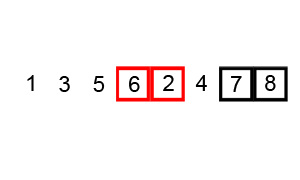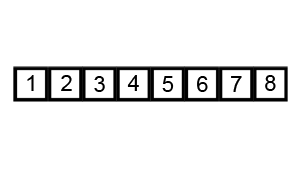
Первый проход:

(5 1 4 2 8) (1 5 4 2 8), Здесь алгоритм сравнивает два первых элемента и меняет их местами.

(1 5 4 2 8) (1 4 5 2 8), Меняет местами, так как [math]\displaystyle{ 5\gt 4 }[/math]

(1 4 5 2 8) (1 4 2 5 8), Меняет местами, так как [math]\displaystyle{ 5\gt 2 }[/math]

(1 4 2 5 8) (1 4 2 5 8), Теперь, ввиду того, что элементы стоят на своих местах ([math]\displaystyle{ 8\gt 5 }[/math]), алгоритм не меняет их местами.

Второй проход:

(1 4 2 5 8) (1 4 2 5 8)

(1 4 2 5 8) (1 2 4 5 8), Меняет местами, так как [math]\displaystyle{ 4\gt 2 }[/math]

(1 2 4 5 8) (1 2 4 5 8)

Теперь массив полностью отсортирован, но алгоритму это неизвестно. Поэтому ему необходимо сделать полный проход и определить, что перестановок элементов не было.

Третий проход:

(1 2 4 5 8) (1 2 4 5 8)

(1 2 4 5 8) (1 2 4 5 8)

Теперь массив отсортирован и алгоритм может быть завершён.

Ссылки

• Динамическая визуализация 7 алгоритмов сортировки с открытым исходным кодом
• Шаблон:Source