Подпись Нюберг — Руэппеля

Эта статья находится на начальном уровне проработки, в одной из её версий выборочно используется текст из источника, распространяемого под свободной лицензией
Материал из энциклопедии Руниверсалис

Подпись Нюберг — Руэппеля (англ. Nyberg-Rueppel Signature Scheme) — схема электронной подписи с использованием открытого ключа, основанная на задаче дискретного логарифмирования в конечном поле. Алгоритм не может использоваться для шифрования (в отличие от RSA и схемы Эль-Гамаля). Подпись создается секретно, но может быть публично проверена. Это значит, что только один субъект может создать подпись сообщения, но любой может проверить её корректность. Схема была предложена Кайсой Нюберг[англ.] и Райнером Руэппелем в 1993 году на первой конференции ACM (англ. 1st ACM conference on Computer and communications security)[1] как модификация DSA[2][3].

Использование алгоритма

Схема подписи с восстановлением сообщения подразумевает собой процедуру, когда сообщение восстанавливается после проверки подписи. Иными словами, пусть имеются два пользователя, Алиса и Боб, и незащищенный канал связи между ними. Пользователь Алиса подписывает открытое сообщение секретным ключом, а полученную подпись пересылает пользователю Бобу, который в свою очередь с помощью открытого ключа проверяет подлинность подписи и восстанавливает сообщение. При положительном результате проверки, Боб убеждается в целостности сообщения, в его оригинальности (то есть в том, что сообщение было послано именно пользователем Алисой), а также лишается возможности утверждать, что Алиса не посылала это сообщение. Важно, что только Алиса способна подписать своё сообщение, потому что только она знает свой секретный ключ, и то, что её подпись может быть проверена любым пользователем, так как для этого нужен лишь открытый ключ[4].

Параметры схемы цифровой подписи

Для построения системы цифровой подписи и генерации ключей необходимо[2][5][6]:

  1. Выбрать открытую функцию избыточности [math]\displaystyle{ f }[/math], которая преобразует фактическое сообщение в данные, которые затем подписываются. Это похоже на хеш-функцию в схемах подписи с приложением, но в отличие от них, функция избыточности должны быть легко обратима.
  2. Выбрать большое простое число [math]\displaystyle{ Q }[/math].
  3. Выбрать большое простое число [math]\displaystyle{ P }[/math], такое, что [math]\displaystyle{ (P-1) }[/math] делится на [math]\displaystyle{ Q }[/math].
  4. Сгенерировать случайное число [math]\displaystyle{ H\lt P }[/math] и вычислить [math]\displaystyle{ G=H^{(P-1)/Q}\mod P }[/math]. Если [math]\displaystyle{ G = 1 }[/math], то искать другое случайное [math]\displaystyle{ H }[/math], пока [math]\displaystyle{ G }[/math] будет не равным [math]\displaystyle{ 1 }[/math], что обеспечит выполнение условия [math]\displaystyle{ G^Q = 1\mod P }[/math]

Открытый и секретный ключи

  1. Секретный ключ представляет собой число [math]\displaystyle{ x \in (0, Q) }[/math]
  2. Открытый ключ вычисляется по формуле [math]\displaystyle{ Y=G^x\mod p }[/math]

Открытыми параметрами являются [math]\displaystyle{ (P, Q, G, Y) }[/math]. Закрытый параметр — [math]\displaystyle{ x }[/math]. Ключевая пара [math]\displaystyle{ (Y, x) }[/math][2][5][6].

Подпись сообщения

Подпись сообщения выполняется по следующему алгоритму[2][5][6]:

  1. Выбрать случайное число [math]\displaystyle{ k \in \mathbb{Z}/Q\mathbb{Z} }[/math] и найти [math]\displaystyle{ R = G^k (mod P) }[/math].
  2. Найти [math]\displaystyle{ E = f(M)\cdot R (mod P) }[/math].
  3. Определить [math]\displaystyle{ S = x\cdot E+k (mod Q) }[/math].

Подписью является пара [math]\displaystyle{ (E, S) }[/math].

Проверка подписи и восстановление сообщения

Исходя из пары [math]\displaystyle{ (E, S) }[/math] и целого числа по модулю [math]\displaystyle{ Q }[/math] необходимо убедиться в том, что подпись принадлежит пользователю с открытым ключом [math]\displaystyle{ Y }[/math] и восстановить сообщение [math]\displaystyle{ M }[/math]. Проверка подписи выполняется по алгоритму:

  1. Вычислить [math]\displaystyle{ U_1 = G^S\cdot Y^{-E} = G^{S-Ex} = G^k (mod P) }[/math].
  2. Вычислить [math]\displaystyle{ U_2 = {E \over U_1} (mod P) }[/math].

Теперь нужно убедиться в том, что [math]\displaystyle{ U_2 }[/math] является значением функции избыточности, то есть [math]\displaystyle{ U_2 = f(M) }[/math]. Если равенство не выполняется, то подпись ложная и отклоняется. В ином случае восстанавливается сообщение [math]\displaystyle{ M = f^{-1}(U_2) }[/math] и принимается подпись[2][5][6].

Схема алгоритма

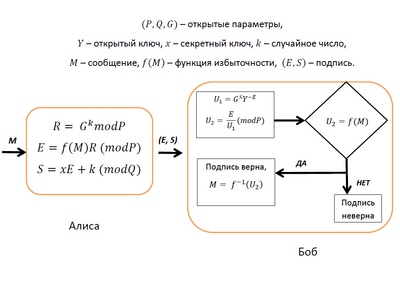
Схема подписи Нюберга — Руэппеля
Схема подписи Нюберга — Руэппеля

Достоинства и недостатки схемы

Схема подписи на тех же принципах, что и DSA, главное отличие заключается в том, что в схеме реализовано восстановление сообщения из подписи. В отличие от RSA, подпись и восстановление не коммутируют, следовательно, алгоритм не может быть использован для шифрования. Преимущества восстановления сообщения заключаются в том, что применение схемы осуществляется без использования хеш-функций, более короткая подпись на коротких сообщениях, возможность прямого применения в схемах на основе идентификационной системы с открытым ключом, где пользователь после регистрации в центре ключей может аутентифицировать себя любому другому пользователю без дальнейшего обращения в центр ключей, или в протоколах согласования ключа, которые устанавливают общий ключ между двумя сторонами на основе взаимной аутентификации[2][7][8].

Пример

Подпись сообщения[9]
  1. Выберем параметры схемы: [math]\displaystyle{ Q = 101, P = 607, G = 601. }[/math]
  2. Ключевая пара пусть выглядит как [math]\displaystyle{ (391, 3) }[/math].
  3. Чтобы подписать сообщение [math]\displaystyle{ M = 12 }[/math] , вычисляем временный ключ [math]\displaystyle{ k = 45 }[/math] и [math]\displaystyle{ R = G^k (mod P) = 143 }[/math].
  4. Пусть [math]\displaystyle{ f(M) = M + 2^4\cdot M }[/math], тогда [math]\displaystyle{ f(M) = 204 }[/math] и

[math]\displaystyle{ E = f(M)\cdot R (mod P) = 36 }[/math], [math]\displaystyle{ S = x\cdot E + k (mod Q) = 52 }[/math].

Итого, пара чисел [math]\displaystyle{ (E, S) }[/math], то есть [math]\displaystyle{ (36, 52) }[/math] — это подпись.

Проверка подписи и восстановление сообщения[9]
  1. Вычисляем [math]\displaystyle{ U_1 = G^{S}\cdot Y^{-E} = 143 }[/math]. Следует заметить, что значение [math]\displaystyle{ U_1 }[/math] совпадает со значением [math]\displaystyle{ R }[/math].
  2. Вычисляем [math]\displaystyle{ U_2 = {E \over U_1} (mod P) = 204 }[/math].
  3. Теперь нужно проверить, что [math]\displaystyle{ U_2 = 204 }[/math] представляется в виде [math]\displaystyle{ M + 2^4\cdot M }[/math] для некоторого целого числа [math]\displaystyle{ M }[/math], и убедившись в этом, делаем заключение в корректности подписи.
  4. Восстанавливаем сообщение [math]\displaystyle{ M = 12 }[/math] как решение уравнения [math]\displaystyle{ M + 2^4\cdot M = 204 }[/math].

См. также

Примечания

  1. ↑ ACM Conference on Computer and Communications Security (CCS). Дата обращения: 9 декабря 2014. Архивировано 10 февраля 2019 года.
  2. ↑ 2,0 2,1 2,2 2,3 2,4 2,5 Nyberg, K., Rueppel, R. A., 1993.
  3. ↑ Elgamal, 1985.
  4. ↑ Смарт, 2005, p. 261.
  5. ↑ 5,0 5,1 5,2 5,3 Nyberg, K., Rueppel, R. A., 1996.
  6. ↑ 6,0 6,1 6,2 6,3 Смарт, 2005, с. 278.
  7. ↑ Смарт, 2005, с. 271.
  8. ↑ Бауер, 2007, с. 228.
  9. ↑ 9,0 9,1 Смарт, 2005, с. 279.

Литература

  • Бауер Ф. Расшифрованные секреты. Методы и принципы криптологии. — Мир, 2007. — 550 с.
  • Смарт, Н. Криптография. — Техносфера, 2005. — 528 с.
  • Elgamal, T. A public key cryptosystem and a signature scheme based on discrete logarithms // Advances in Cryptology : книга. — 1985.
  • Nyberg, K., Rueppel, R. A. Message Recovery for Signature Schemes Based on the Discrete Logarithm Problem // Designs, Codes and Cryptography : журнал. — 1996. — № Volume 7, Issue 1-2. — С. 61-81.
  • Nyberg, K., Rueppel, R. A. A new signature scheme based on the DSA giving message recovery // 1st ACM Conference on Computer and Communications Security, Fairfax, Virginia (Nov. 3–5, 1993). — 1993.


Источник — https://xn--h1ajim.xn--p1ai/index.php?title=Подпись_Нюберг_—_Руэппеля&oldid=5858042