Переменная типа RR Лиры
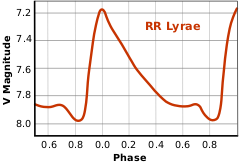
Переменные типа RR Лиры — класс пульсирующих переменных звёзд, прототипом которого стала звезда RR Лиры. Такие звёзды довольно старые и маломассивные, и встречаются в основном в шаровых скоплениях. Светимости всех звёзд типа RR Лиры практически одинаковы, поэтому они используются как стандартные свечи[1].
История изучения
Переменные типа RR Лиры впервые открыл Солон Ирвинг Бейли в 1895 году, изучая шаровое звёздное скопление Омега Центавра. В течение следующих 20 лет он открыл и исследовал множество переменных звёзд в шаровых скоплениях, ввёл их классификацию на основе формы их кривых блеска, с некоторыми изменениями используемую и поныне[2][3].
В 1899 году Вильямина Флеминг открыла саму звезду RR Лиры, ставшую прототипом этого класса, и в 1901 обнаружила её переменность[2][4].
В начале XX века Сергей Блажко обнаружил, что форма кривой блеска и амплитуда изменения яркости у звёзд XZ Лебедя и RW Дракона меняется. Это явление получило название эффекта Блажко[2].
Альтернативные названия
Переменные типа RR Лиры в больших количествах встречаются в шаровых скоплениях, из-за чего их раньше называли переменными шаровых скоплений. В прошлом также было распространено название «короткопериодические цефеиды» из-за сходства их кривых блеска с кривыми блеска цефеид: у обоих классов звёзд наблюдаются быстрый рост яркости и более медленный спад. Однако это название не учитывает серьёзные физические различия звёзд, и поэтому не используется. Наконец, известно другое устаревшее название: «анталголи». Здесь также имеется в виду форма кривой блеска: затменные звёзды, в частности, Алголь, большую часть времени находятся в максимуме яркости, и малую часть времени в минимуме, а звёзды типа RR Лиры — наоборот[1][2].
Характеристики
Переменные типа RR Лиры являются гигантами спектрального класса А, лежащими на горизонтальной ветви диаграммы Герцшпрунга — Рассела. Светимости таких звёзд различаются слабо, составляют порядка 40 L⊙ (абсолютные звёздные величины — обычно 0,4-0,8m) и зависят в основном от металличности[2][5]:
- [math]\displaystyle{ M = 0.2[\text{Fe/H}] + 1.0. }[/math]
Поэтому переменные типа RR Лиры используются как стандартные свечи. Массы переменных типа RR Лиры составляют около 0,7 M⊙. При такой массе высокая светимость обусловлена тем, что эти звёзды находятся на более поздних стадиях эволюции: такие звёзды имеют возраст более 12 миллиардов лет. Таким образом, это старые звёзды, принадлежащие населению II, содержащие мало тяжёлых элементов и расположенные в сферической подсистеме Галактики. Такие звёзды встречаются в шаровых скоплениях, но не в рассеянных, так как последние распадаются гораздо быстрее, при этом в двойных звёздах они практически не встречаются. Так как переменные звёзды, как правило, не отмечаются на диаграмме Герцшпрунга — Рассела, звёзды RR Лиры образуют так называемый пробел Шварцшильда[1][2][5][6][7][8].
Периоды пульсаций таких звёзд составляют 0,2-1,2 суток, а амплитуды изменения блеска — до 2m. Кривые блеска характеризуются быстрым ростом светимости и медленным спадом. Как и у цефеид, максимум светимости совпадает с максимумом температуры[1][5]. Кроме того, у некоторых переменных типа RR Лиры наблюдается эффект Блажко: периодическое изменение формы кривой блеска и её амплитуды. Период таких изменений обычно на два порядка больше периода пульсаций звезды, и, по-видимому, они вызваны пульсациями магнитного поля звезды. Эффект Блажко, по всей видимости, не связан с эволюционными изменениями — по расчётам, изменение периода переменности в результате эволюции должно составлять около 0,1 суток за миллион лет[2].
Ещё одна особенность переменных типа RR Лиры заключается в том, что при оценке спектрального класса по различным линиям получаются различные результаты. Для количественного выражения этого различия используется так называемый индекс Престона [math]\displaystyle{ \text{D}S }[/math][2]:
- [math]\displaystyle{ \text{D}S = -10[\text{Sp(Ca II)} - \text{Sp(H)}], }[/math]
то есть берётся разность спектрального класса, определённого по линиям ионизованного кальция и по линиям водорода и умножается на 10. К примеру, если водородный спектральный класс — A8, а кальциевый — A5, то [math]\displaystyle{ \text{D}S = 3 }[/math]. Индекс Престона для различных звёзд этого класса обычно варьируется от 0 до 10, следовательно, различие может достигать целого спектрального класса. Оказалось, что этот индекс, в свою очередь, связан с содержанием тяжёлых элементов в звезде — металличности таких переменных варьируются от практически солнечных до меньших солнечной на три порядка[2][5].
Классификация
В Общем каталоге переменных звёзд переменные типа RR Лиры делятся на два типа[2][3]:
- RRAB — переменные с асимметричной кривой блеска (более крутой восходящей ветвью), периодами от 0,3 до 1,2 дней и амплитудами от 0,5m до 2m (пример — RR Лиры). Первоначально Бейли ввёл два класса: RRa и RRb, отличавшиеся крутизной восходящей ветви, однако впоследствии оказалось, что чёткой грани между ними нет, и они были объединены.
- RRC — переменные c более симметричными, похожими на синусоидальные, кривыми блеска и периодами от 0,2 до 0,4 дней и амплитудами, не превышающими 0,5m (пример — SX UMa). В современной теории звёздных пульсаций считается, что, в отличие от подтипа RRab (пульсирующего в основном тоне), звёзды подтипа RRc пульсируют в обертоне.
Физика явления
Механизм пульсаций
Обычно звёзды находятся в термодинамическом равновесии, то есть внутреннее давление газа в звезде и её собственный вес уравновешены. Если оно нарушается, например, звезда расширяется или сжимается, она стремится вернуться в состояние равновесия и в ней начинаются колебания. Период таких колебаний [math]\displaystyle{ P }[/math] связан с плотностью звезды [math]\displaystyle{ \rho }[/math] следующим образом[7][9]:
- [math]\displaystyle{ P = \frac{1}{\sqrt{G\rho}}, }[/math]
где [math]\displaystyle{ G }[/math] — гравитационная постоянная. Например, для Солнца имеющего среднюю плотность 1,4 г/см3 период будет составлять немногим меньше часа[9].
Если обычная звезда по каким-то причинам потеряет равновесие, то она начнёт колебаться, но эти колебания быстро затухнут. Наблюдения пульсирующих переменных показывают, что их колебания не затухают, а значит, они должны иметь какой-то источник энергии. В 1917 году Артур Эддингтон предложил механизм, в настоящее время общепринятый, который носит название «каппа-механизм» или «клапан Эддингтона»[9][10].
Сам механизм заключается в следующем: в пульсирующих переменных имеется слой ионизованного гелия толщиной в 1-2 % радиуса звезды. He III (дважды ионизованный гелий) менее прозрачен, чем He II (однократно ионизованный гелий), и, чем больше температура, тем бо́льшая часть гелия становится дважды ионизованной. Из-за этого слой гелия становится менее прозрачным, он начинает задерживать энергию и при этом нагреваться, из-за чего звезда расширяется. При расширении температура слоя гелия снова падает, происходит частичная рекомбинация He III и превращение его в He II и он становится более прозрачным, пропуская лучистую энергию во внешние слои. Из-за этого давление во внутренних слоях звезды падает, под действием силы тяжести звезда опять сжимается, и процесс повторяется[9].
Кроме того, каппа-механизм пульсации возможен не у всех звёзд. Пульсировать могут звёзды лишь с определёнными температурами, и такие звёзды на диаграмме Герцшпрунга — Рассела образуют полосу нестабильности[9].
Эволюционная стадия звёзд типа RR Лиры
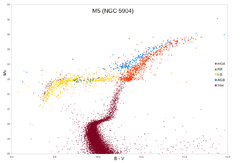
На наиболее длительном этапе жизни звезды — главной последовательности — звёзды сжигают водород в ядре, но в определённый момент он заканчивается. Звезда сходит с главной последовательности, проходит стадию субгиганта и красного гиганта, после чего в звёздах с массами менее 2,5-3 M⊙ происходит гелиевая вспышка — взрывообразный запуск реакций с участием гелия, и звезда переходит на так называемую горизонтальную ветвь[7][11].
Звёзды горизонтальной ветви имеют практически одинаковые светимости, но различные температуры поверхности. На диаграмме Герцшпрунга — Рассела через горизонтальную ветвь проходит полоса нестабильности и на их пересечении нет звёзд с постоянным блеском — эта область получила название «пробел Шварцшильда». Переменные типа RR Лиры находятся именно в этом пробеле, и для того, чтобы в него попасть сразу после гелиевой вспышки или спустя какое-то время, звёзды должны иметь определённую начальную массу — 0,8—0,9 M⊙, так как в ходе эволюции такая звезда теряет 0,1-0,2 M⊙ — и определённый возраст, так как срок жизни звезды напрямую зависит от её массы[2][7][12].
Связь параметров шаровых скоплений и переменных типа RR Лиры
Не все шаровые скопления одинаково богаты переменными типа RR Лиры: к примеру, в скоплении M 13 таких переменных практически нет, так как звёзды горизонтальной ветви там слишком горячие. Наоборот, в скоплении 47 Тукана вся горизонтальная ветвь лежит в области более низких температур, и звёзд типа RR Лиры там тоже практически нет. Морфология горизонтальной ветви для скопления зависит от содержания в нём тяжёлых элементов: чем ниже металличность скопления, тем более голубой будет горизонтальная ветвь. Тем не менее, хотя зависимость металличности и положения горизонтальной ветви хорошо прослеживается, параметры скоплений имеют довольно большой разброс относительно неё. Это значит, что на морфологию горизонтальной ветви влияет какой-то другой параметр или их совокупность. Считается, что может влиять количество углерода, азота и кислорода в звёздах или другие параметры, однако пока что не удалось полностью объяснить всё наблюдаемое разнообразие шаровых скоплений. Таким образом, остаётся нерешённой проблема второго параметра (или «проблема третьего параметра», если учитывать влияние возраста скопления)[2][13].
Также при изучении шаровых скоплений была обнаружена следующая особенность: если для каждого скопления с достаточным количеством переменных типа RR Лиры усреднить периоды переменных подтипа RRAB, то скопления могут быть разделены на два класса: первый (Oo I, пример — M 3) будет иметь средний период около 0,55 суток, а второй (Oo II, пример — M 15) — около 0,65 суток. Это явление получило название «эффект Оостерхоффа». Несмотря на то, что некоторый разброс этих значений всё же присутствует, в Млечном Пути не обнаружено скоплений с промежуточным значением усреднённого периода[2].
Примечания
- ↑ 1,0 1,1 1,2 1,3 Кононович Э.В., Мороз В.И. Общий курс астрономии. — 2-е, исправленное. — УРСС, 2004. — С. 404. — 544 с. — ISBN 5-354-00866-2.
- ↑ 2,00 2,01 2,02 2,03 2,04 2,05 2,06 2,07 2,08 2,09 2,10 2,11 2,12 Самусь Н.Н. Переменные типа RR Лиры. Типы по ОКПЗ: RRAB, RRC, RR(B).. Дата обращения: 18 июня 2010. Архивировано 3 февраля 2021 года.
- ↑ 3,0 3,1 5.2 Переменные звезды в шаровых скоплениях. Астронет. Астронет. Дата обращения: 13 июня 2020. Архивировано 13 июня 2020 года.
- ↑ Burnham, Robert, Jr. (1978), Burnham's Celestial Handbook, vol. 2, New York: Dover Publications, ISBN 0-486-23568-8, <https://books.google.com/books?id=wB9uZ9lH5bgC&pg=PA1154> Архивная копия от 12 августа 2020 на Wayback Machine
- ↑ 5,0 5,1 5,2 5,3 Horace A. Smith. RR Lyrae Stars. — С. 9—15. — 156 с. Архивная копия от 13 июня 2020 на Wayback Machine
- ↑ Layden, A. C.; Hanson, Robert B.; Hawley, Suzanne L.; Klemola, Arnold R.; Hanley, Christopher J. The Absolute Magnitude and Kinematics of RR Lyrae Stars via Statistical Parallax (англ.) // Astron. J. : journal. — 1996. — August (vol. 112). — P. 2110—2131. — doi:10.1086/118167. — . — arXiv:astro-ph/9608108.
- ↑ 7,0 7,1 7,2 7,3 Hannu Karttunen, Pekka Kröger, Heikki Oja, Markku Poutanen, Karl Johan Donner. Fundamental Astronomy. — Springer, 2007. — С. 249—254, 282. — 510 с. — ISBN 978-3-540-00179-9. Архивная копия от 5 июня 2020 на Wayback Machine
- ↑ Hajdu, G.; Catelan, M.; Jurcsik, J.; Dékány, I.; Drake, A.J.; Marquette, B. New RR Lyrae variables in binary systems (англ.) // Monthly Notices of the Royal Astronomical Society : journal. — Oxford University Press, 2015. — Vol. 449, no. 1. — P. L113–L117. — doi:10.1093/mnrasl/slv024. — . — arXiv:1502.01318.
- ↑ 9,0 9,1 9,2 9,3 9,4 Кононович Э.В., Мороз В.И. Общий курс астрономии. — 2-е, исправленное. — УРСС, 2004. — С. 402—403. — 544 с. — ISBN 5-354-00866-2.
- ↑ Smith, D. H. Eddington's Valve and Cepheid Pulsations (англ.) // Sky and Telescope : magazine. — 1984. — Vol. 68. — P. 519. — .
- ↑ Salaris, Maurizio; Cassisi, Santi. Evolution of Stars and Stellar Populations // Evolution of Stars and Stellar Populations. — 2005. — .
- ↑ Кононович Э.В., Мороз В.И. Общий курс астрономии. — 2-е, исправленное. — УРСС, 2004. — С. 400. — 544 с. — ISBN 5-354-00866-2.
- ↑ Звездная астрономия в лекциях. Астронет. Дата обращения: 23 февраля 2021. Архивировано 3 февраля 2021 года.
Ссылки
- Robert Nemiroff & Jerry Bonnell. M3: изменчивое шаровое скопление. Астронет / Astronomy Picture Of the Day. Астронет.