Отдача от масштаба

Отдача от масштаба (англ. returns to scale) — показатель, определяющий объем выпуска от изменения масштаба производства. Если увеличивается количество всех факторов в одно и то же число [math]\displaystyle{ a }[/math]—раз и объем выпуска возрастает также в [math]\displaystyle{ a }[/math]—раз, то это функция с постоянной отдачей от масштаба. Если выпуск возрастает более чем в [math]\displaystyle{ a }[/math]—раз, то это возрастающая отдача от масштаба. Если выпуск возрастает менее чем в [math]\displaystyle{ a }[/math]—раз — это убывающая отдача от масштаба.

Определение

Согласно Британнике отдача от масштаба — это количественные изменения в производстве фирмы или отрасли в результате пропорционального увеличения всех затрат (факторов производства).

Отдача от масштаба и эффект масштаба взаимосвязаны, но имеют разные концепции того, что происходит по мере увеличения масштаба производства в долгосрочном периоде, когда все уровни затрат, включая использование физического капитала, являются переменными (выбираются предприятием). Отдача от масштаба возникает в контексте производственной функции предприятия, объясняется поведением темпа роста выпуска (производства) относительно связанного с ним увеличения затрат (факторов производства) в долгосрочном периоде. В долгосрочном периоде все факторы производства изменчивы и могут изменяться в связи с определенным увеличением размера (масштаба). Эффект масштаба показывает влияние повышения уровня производства на единицу затрат, а отдача от масштаба определяется только соотношением между объемами используемых ресурсов и выпуском.

Однородность производственной функции

Производственная функция называется однородной, если при увеличении количества всех производственных ресурсов в [math]\displaystyle{ a }[/math] раз выпуск увеличивается в [math]\displaystyle{ a }[/math] раз, то есть [math]\displaystyle{ \ F(aK,aL)=aF(K,L) }[/math]. Показатель [math]\displaystyle{ a }[/math] определяет степень однородности функции, и если равенство для данной производственной функции не выполняется, то производственная функция — неоднородная. Где [math]\displaystyle{ K }[/math] — это единица капитала, [math]\displaystyle{ L }[/math] — единица рабочей силы, [math]\displaystyle{ a }[/math] — параметр увеличение/уменьшение в [math]\displaystyle{ a }[/math]—раз, тогда для производственной функции [math]\displaystyle{ \ F(K,L) }[/math] при [math]\displaystyle{ a \gt 1 }[/math]:

• [math]\displaystyle{ \ F(aK,aL)\gt aF(K,L) }[/math] — возрастающая отдача от масштаба;
• [math]\displaystyle{ \ F(aK,aL)=aF(K,L) }[/math] — постоянная отдача от масштаба;
• [math]\displaystyle{ \ F(aK,aL)\lt aF(K,L) }[/math] — убывающая отдача от масштаба.

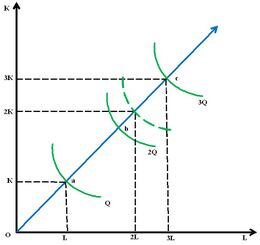
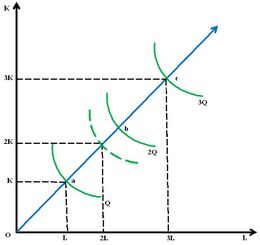
На рисунках 1, 2, 3 лучи, проведенные из начала координат, являются линиями роста. Линия роста определяет технически возможные пути расширения производства предприятия, переход с более низкой на более высокую изокванту. Среди возможных линий роста — изоклиналь, вдоль которой предельная норма технического замещения ресурсов при любом объеме выпуска постоянна. Для однородной производственной функции изоклиналь представляется лучом, проведенным из начала координат, вдоль которого предельная норма технического замещения и соотношение [math]\displaystyle{ K/L }[/math] имеют одно и то же значение.

Рисунок 1. Постоянная отдача от масштаба Рисунок 2. Возрастающая отдача от масштаба Рисунок 3. Убывающая отдача от масштаба

См. также

• Эффект масштаба
• Эффект охвата
• Дезэкономия
• Экономия на плотности