Осциллятор Дуффинга
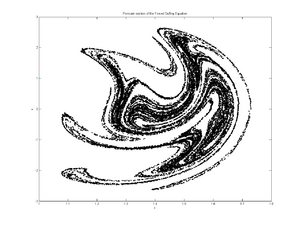
Осциллятор Дуффинга (англ. Duffing oscillator) — простейшая одномерная нелинейная система. Представляет собой одномерную частицу, движущуюся в потенциале [math]\displaystyle{ U(x)=ax^2/2+bx^4/4 }[/math]. При [math]\displaystyle{ b=0 }[/math] система сводится к обычному гармоническому осциллятору. Особенностью осциллятора Дуффинга является возможность получения хаотической динамики.
Уравнение движения для осциллятора Дуффинга имеет вид
- [math]\displaystyle{ m\ddot{x} = -ax -bx^3 }[/math],
где [math]\displaystyle{ x }[/math] и [math]\displaystyle{ m }[/math], соответственно — координата частицы и её масса. Уравнение впервые было изучено немецким инженером Георгом Дуффингом в 1918 году. Дискретная его версия известна как отображение Дуффинга[англ.].
Решение осциллятора Дуффинга выражается через эллиптические функции: [math]\displaystyle{ x(t) = a_{1}cn(u,k), u=a_{2}t+b }[/math].[1]
Зависимость амплитуды от частоты
В отсутствие диссипации (трения), гармонический (линейный) осциллятор, находящийся под действием внешней периодической силы [math]\displaystyle{ F = F_0 \cos (\omega t) }[/math], испытывает резонанс, если частота этой силы [math]\displaystyle{ \omega }[/math] совпадает с собственной частотой осциллятора [math]\displaystyle{ \omega_0 = \omega }[/math]. Вблизи резонанса осциллятор совершает колебания конечной амплитуды. Последняя пропорциональна [math]\displaystyle{ (\omega_0 - \omega)^{-2} }[/math] и расходится точно в резонансе.
В отличие от гармонического осциллятора, осциллятор Дуффинга под действием внешней периодической силы испытывает бистабильное поведение.
Примечания
- ↑ Rand, R.H. Lecture notes on nonlinear vibrations // Cornell Universit. — 2012. — С. 13–17. Архивировано 23 сентября 2021 года.
Литература
- Ivana Kovacic, Michael J Brennan. The Duffing Equation : Nonlinear Oscillators and their Behaviour. — John Wiley & Sons, 2011. — ISBN 9780470715499.
- M. Lakshmanan, K Murali. Chaos In Nonlinear Oscillators: Controlling And Synchronization. — World Scientific, 1996. — Vol. 13. — P. 35—90. — 340 p. — (World Scientific Series on Nonlinear Science Series A). — ISBN 978-981-02-2143-0.