Частичный предел последовательности
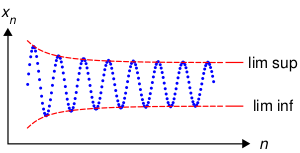
Частичный предел некоторой последовательности — это предел одной из её подпоследовательностей, если только он существует. Для сходящихся числовых последовательностей частичный предел совпадает с обычным пределом в силу единственности последнего, однако в самом общем случае у произвольной последовательности может быть от нуля до бесконечного числа различных частичных пределов. При этом, если обычный предел характеризует точку, к которой элементы последовательности приближаются с ростом номера, то частичные пределы характеризуют точки, вблизи которых лежит бесконечно много элементов последовательности.
Два важных частных случая частичного предела — верхний и нижний пределы.
Определения
Частичным пределом последовательности называется предел какой-либо её подпоследовательности, если существует хотя бы одна подпоследовательность, имеющая предел. В противном случае, говорят, что у последовательности нет частичных пределов. В некоторой литературе в случаях, если из последовательности удаётся выделить бесконечно большую подпоследовательность, все элементы которой одновременно положительны или отрицательны, её частичным пределом называют соответственно [math]\displaystyle{ +\infty }[/math] или [math]\displaystyle{ -\infty }[/math].
Нижний предел последовательности — это точная нижняя грань множества частичных пределов последовательности.
Верхний предел последовательности — это точная верхняя грань множества частичных пределов последовательности.
Иногда нижним пределом последовательности называют наименьшую из её предельных точек, а верхним — наибольшую.[1] Эти определения эквивалентны, так как точная грань множества предельных точек обязательно принадлежит этому множеству.
Обозначения
Нижний предел последовательности [math]\displaystyle{ \left\{ x_n \right\}_{n = 1}^{\infty} }[/math]:
- [math]\displaystyle{ \varliminf_{n \to \infty} x_n }[/math] (в отечественной литературе);
- [math]\displaystyle{ \liminf_{n \to \infty} x_n }[/math] (в иностранной литературе).
Верхний предел последовательности [math]\displaystyle{ \left\{ x_n \right\}_{n = 1}^{\infty} }[/math]:
- [math]\displaystyle{ \varlimsup_{n \to \infty} x_n }[/math] (в отечественной литературе);
- [math]\displaystyle{ \limsup_{n \to \infty} x_n }[/math] (в иностранной литературе).
Примеры
- [math]\displaystyle{ \varliminf_{n \to \infty} \frac{1}{n} = \varlimsup_{n \to \infty} \frac{1}{n} = \lim_{n \to \infty} \frac{1}{n} = 0 }[/math]
- [math]\displaystyle{ \varliminf_{n \to \infty} \left( -1 \right)^n = -1 }[/math]
- [math]\displaystyle{ \varlimsup_{n \to \infty} \left( -1 \right)^n = +1 }[/math]
- [math]\displaystyle{ \nexists \varliminf_{n \to \infty} n, \nexists \varlimsup_{n \to \infty} n }[/math] (в другой терминологии оба предела равны [math]\displaystyle{ +\infty }[/math])
Свойства
- Частичным пределом последовательности может быть только её предельная точка, и, наоборот, любая предельная точка последовательности представляет собой некоторый её частичный предел. Иными словами, понятия «частичный предел последовательности» и «предельная точка последовательности» эквивалентны[a].
- У любой ограниченной последовательности существуют и верхний, и нижний пределы (в множестве вещественных чисел). Если же считать [math]\displaystyle{ -\infty }[/math] и [math]\displaystyle{ +\infty }[/math] допустимыми значениями частичного предела, то верхний и нижний пределы существуют вообще у любой числовой последовательности.
- Числовая последовательность [math]\displaystyle{ \{x_n\} }[/math] сходится к [math]\displaystyle{ a }[/math] тогда и только тогда, когда [math]\displaystyle{ \varliminf_{n\rightarrow\infty}{x_{n}}=\varlimsup_{n\rightarrow\infty}{x_{n}}=a }[/math].
- Для любого наперёд взятого положительного числа [math]\displaystyle{ \varepsilon }[/math] все элементы ограниченной числовой последовательности [math]\displaystyle{ \left\{ x_n \right\}_{n = 1}^{\infty} }[/math], начиная с некоторого номера, зависящего от [math]\displaystyle{ \varepsilon }[/math], лежат внутри интервала [math]\displaystyle{ \left(\varliminf_{n \to \infty} x_n - \varepsilon, \varlimsup_{n \to \infty} x_n + \varepsilon \right) }[/math].
- Если за пределами интервала [math]\displaystyle{ \left( a, b \right) }[/math] лежит лишь конечное число элементов ограниченной числовой последовательности [math]\displaystyle{ \left\{ x_n \right\}_{n = 1}^{\infty} }[/math], то интервал [math]\displaystyle{ \left(\varliminf_{n \to \infty} x_n, \varlimsup_{n \to \infty} x_n \right) }[/math] содержится в интервале [math]\displaystyle{ \left( a, b \right) }[/math].
- Множество частичных пределов замкнуто.
Примечания
Комментарии
- ↑ При этом следует помнить, что элемент, встречающийся в последовательности бесконечное число раз, является предельной точкой этой последовательности (в отличие от предельной точки множества).
Источники
- ↑ В. А. Ильин, В. А. Садовничий, Бл. Х. Сендов. Глава 3. Теория пределов // Математический анализ / Под ред. А. Н. Тихонова. — 3-е изд., перераб. и доп. — М.: Проспект, 2006. — Т. 1. — С. 92 — 105. — 672 с. — ISBN 5-482-00445-7.