Метод симметричных составляющих
Метод симметричных составляющих — метод расчёта несимметричных электрических систем, основанный на разложении несимметричной системы на три симметричные — прямую, обратную и нулевую. Метод широко применяется для расчёта несимметричных режимов трёхфазной сети, например, коротких замыканий.
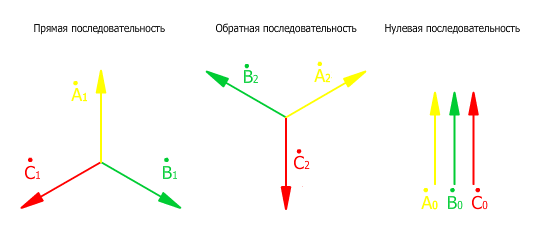
Разложение
Прямая последовательность
Прямую последовательность составляют три вектора [math]\displaystyle{ \bar A_1 }[/math], [math]\displaystyle{ \bar B_1 }[/math] и [math]\displaystyle{ \bar C_1 }[/math], имеющие одинаковый модуль и сдвинутые друг относительно друга на 120o. Вектор [math]\displaystyle{ \bar A_1 }[/math] опережает вектор [math]\displaystyle{ \bar B_1 }[/math], а вектор [math]\displaystyle{ \bar B_1 }[/math] опережает вектор [math]\displaystyle{ \bar C_1 }[/math].
Обратная последовательность
Обратную последовательность составляют векторы [math]\displaystyle{ \bar A_2 }[/math], [math]\displaystyle{ \bar B_2 }[/math] и [math]\displaystyle{ \bar C_2 }[/math], одинаковой длины и сдвинутые друг относительно друга на 120o. Вектор [math]\displaystyle{ \bar C_2 }[/math] опережает вектор [math]\displaystyle{ \bar B_2 }[/math], а вектор [math]\displaystyle{ \bar B_2 }[/math] опережает вектор [math]\displaystyle{ \bar A_2 }[/math].
Нулевая последовательность
Нулевая последовательность образуется векторами [math]\displaystyle{ \bar A_0 }[/math], [math]\displaystyle{ \bar B_0 }[/math] и [math]\displaystyle{ \bar C_0 }[/math] одинаковыми по модулю и направлению.
Расчет
Любая несимметричная система может быть представлена суммой трех симметричных. Таким образом:
[math]\displaystyle{
\begin{cases}
\bar A = \bar A_1+ \bar A_2+\bar A_0\\
\bar B = \bar B_1+ \bar B_2+\bar B_0\\
\bar C = \bar C_1+ \bar C_2+\bar C_0
\end{cases}
}[/math]
Введя оператор a, равный:
[math]\displaystyle{ a = e^{j\tfrac{2\pi}{3}} }[/math],
можно получить для системы:
[math]\displaystyle{
\begin{cases}
\bar A = \bar A_1+ \bar A_2+\bar A_0\\
\bar B = a^2\bar A_1+ a\bar A_2+\bar A_0\\
\bar C = a\bar A_1+ a^2\bar A_2+\bar A_0
\end{cases}
}[/math]
Таким образом получается система из трех уравнений с тремя неизвестными, у которой решение однозначно.
Для значений векторов в составляющих симметричных системах получается:
[math]\displaystyle{ \bar A_1 = \tfrac{1}{3} (\bar A+a\bar B+a^2\bar C) }[/math]
[math]\displaystyle{ \bar A_2 = \tfrac{1}{3} (\bar A+a^2\bar B+a\bar C) }[/math]
[math]\displaystyle{ \bar A_0 = \tfrac{1}{3} (\bar A+\bar B+\bar C) }[/math]
Эти соотношения справедливы для любой системы, в том числе и симметричной. В этом случае:
[math]\displaystyle{ \bar A = \bar A_1 }[/math]; [math]\displaystyle{ \bar A_2 = \bar A_0 = 0 }[/math]
Несимметричные режимы
Составляющие обратной последовательности возникают при появлении в сети любой несимметрии: однофазного или двухфазного короткого замыкания, обрыва фазы, несимметрии нагрузки.
Составляющие нулевой последовательности имеют место при замыканиях на землю (одно- и двухфазных) или при обрыве одной или двух фаз. В случае междуфазного замыкания составляющие нулевой последовательности(токи и напряжения) равны нулю.
Применение метода

- Метод широко применяется для расчета несимметричных режимов работы электроэнергетических систем.
- Этот метод используют многие устройства РЗиА. В частности, принцип работы трансформатора тока нулевой последовательности основан на сложении значений тока во всех трех фазах защищаемого участка. В нормальном(симметричном) режиме сумма значений фазных токов равна нулю. В случае возникновения однофазного замыкания, в сети появятся токи нулевой последовательности и сумма значений токов в трех фазах будет отлична от нуля, что зафиксирует измерительный прибор (например, амперметр), подключенный ко вторичной обмотке трансформатора тока нулевой последовательности.
- Для трехфазных транспозированых ЛЭП результат этого преобразования — точная матрица собственных векторов (матрица модального преобразования)[1]. Она одинакова как для тока, так и для напряжения.
Примечания
- ↑ Prado A. J. do, Kurokawa S., Bovolato L. F., Filho J. P. and Costa E. C. M. da. Phase-Mode Transformation Matrix Application for Transmission Line and Electromagnetic Transient Analyses. — New York : Nova Science Pub, 2011. — P. 40. — ISBN 978-1-61728-486-1.
Литература
- Основы теории цепей : учеб. для вузов / Г. В. Зевеке, П. А. Ионкин, А. В. Нетушил, С. В. Страхов. − 5-е изд., перераб. — М. : Энергоатомиздат, 1989. − 528 с.