Ковариация

Ковариа́ция или корреляционный момент [math]\displaystyle{ \mathrm{cov}(X,Y) }[/math] случайных величин — в теории вероятностей и математической статистике мера зависимости двух случайных величин.

В теории вероятностей и статистике ковариация является мерой совместной изменчивости двух случайных величин. Если большие значения одной переменной в основном соответствуют большим значениям другой переменной, и то же самое верно для меньших значений (то есть переменные имеют тенденцию демонстрировать одинаковое поведение), ковариация положительна.В противоположном случае, когда большие значения одной переменной в основном соответствуют меньшим значениям другой (т. е. переменные имеют тенденцию показывать противоположное поведение), ковариация отрицательна. Таким образом, знак ковариации показывает тенденцию линейной зависимости между переменными. Величину ковариации нелегко интерпретировать, поскольку она не нормирована и, следовательно, зависит от величин переменных. Однако нормализованная версия ковариации, коэффициент корреляции, своей величиной показывает силу линейной зависимости.

Определение

Пусть [math]\displaystyle{ X, Y }[/math] — две случайные величины, определённые на одном и том же вероятностном пространстве. Тогда их ковариация определяется следующим образом:

[math]\displaystyle{ \mathrm{cov}(X,Y) = \mathbb{M} \left[(X - \mathbb{M}X) (Y - \mathbb{M}Y)\right] }[/math],

где [math]\displaystyle{ \mathbb{M} }[/math]— математическое ожидание (в англоязычной литературе принято обозначение [math]\displaystyle{ \mathbb{E} }[/math]).

Предполагается, что все математические ожидания [math]\displaystyle{ \mathbb{M} }[/math] в правой части данного выражения определены.

Замечания

• Если [math]\displaystyle{ X,Y\in L^2 }[/math], то есть имеют конечный второй момент, то ковариация определена и конечна.
• В гильбертовом пространстве несмещённых случайных величин с конечным вторым моментом [math]\displaystyle{ L^2_0 \equiv \{X \in L^2 \mid \mathbb{M}X = 0 \} }[/math] ковариация имеет вид [math]\displaystyle{ \mathrm{cov}(X,Y) = \mathbb{M}[XY] }[/math]и играет роль скалярного произведения.

Выборочный коэффициент ковариации

Пусть [math]\displaystyle{ X_1, X_2, ... ,X_n }[/math] - выборка [math]\displaystyle{ X }[/math] объёма [math]\displaystyle{ n }[/math], [math]\displaystyle{ Y_1, Y_2, ... ,Y_n }[/math] — выборка [math]\displaystyle{ Y }[/math] объёма [math]\displaystyle{ n }[/math] и они порождены случайными величинами, определёнными на одном и том же вероятностном пространстве. Тогда выборочным коэффициентом ковариации является средняя величина произведений отклонений значений от средних значений соответствующих выборок:

[math]\displaystyle{ \overline{s}_{XY}= \mathrm{cov}(X,Y) = {1 \over n}\sum_{t=1}^n \left(X_t-\overline{X}\right)\left(Y_t-\overline{Y}\right) }[/math],

где средние значения выборок (также называемые выборочными средними) определяют по формулам:

[math]\displaystyle{ \overline{X} = \frac1n\sum_{t=1}^n X_t }[/math],

[math]\displaystyle{ \overline{Y} = \frac1n\sum_{t=1}^n Y_t }[/math] .

Если раскрыть скобки и воспользоваться формулой для выборочного среднего, то:

[math]\displaystyle{ \mathrm{cov}(X,Y) = \frac1n\sum_{t=1}^n X_tY_t-\left(\frac1n\sum_{t=1}^nX_t\right)\left(\frac1n\sum_{t=1}^nY_t\right) = \frac1n\sum_{t=1}^n X_tY_t-\overline{X}\overline{Y} }[/math].

Свойства

• Если [math]\displaystyle{ X,Y }[/math] — независимые случайные величины, то

  [math]\displaystyle{ \mathrm{cov}(X,Y) = 0 }[/math].

• Но обратное утверждение, вообще говоря, неверно: из отсутствия ковариации не следует независимость. Пример:

  Пусть случайная величина [math]\displaystyle{ Z }[/math] принимает значения [math]\displaystyle{ 0, \frac{\pi}{2}, \pi }[/math], каждое с вероятностью [math]\displaystyle{ \frac13 }[/math]. Тогда [math]\displaystyle{ \cos{Z} }[/math] будет принимать значения −1, 0 и 1, каждое с вероятностью [math]\displaystyle{ \frac13 }[/math], а [math]\displaystyle{ P(\sin{Z} = 1) = \frac13, P(\sin{Z} = 0) = \frac23, P(\sin{Z} = -1) = 0 }[/math]. Тогда [math]\displaystyle{ \mathrm{cov}(\sin{Z},\cos{Z}) = 0 }[/math], но [math]\displaystyle{ 0 = P(\sin{Z} = 1, \cos{Z} = 1) \ne P(\cos{Z} = 1) P(\sin{Z} = 1) = \frac19 }[/math]

• Ковариация случайной величины с собой равна дисперсии: [math]\displaystyle{ \mathrm{cov}(X,X) = \mathrm{D}[X] }[/math].
• Ковариация симметрична:

  [math]\displaystyle{ \mathrm{cov}(X,Y) = \mathrm{cov}(Y,X) }[/math].

• В силу линейности математического ожидания ковариация может быть записана как

  [math]\displaystyle{ \mathrm{cov}(X,Y) = \mathbb{M} \left[XY - X\mathbb{M}Y - Y\mathbb{M}X + \mathbb{M}X\mathbb{M}Y \right] = }[/math]
  [math]\displaystyle{ \; = \mathbb{M} \left[ XY \right] - \mathbb{M}X \mathbb{M}Y - \mathbb{M}X \mathbb{M}Y + \mathbb{M}X \mathbb{M}Y = }[/math]
  [math]\displaystyle{ \; = \mathbb{M} \left[ XY \right] - \mathbb{M}X \mathbb{M}Y }[/math].

• Пусть [math]\displaystyle{ X_1,\ldots, X_n }[/math] случайные величины, а [math]\displaystyle{ Y_1 = \sum\limits_{i=1}^n a_i X_i,\; Y_2 = \sum\limits_{j=1}^m b_j X_j }[/math] — их две произвольные линейные комбинации. Тогда

  [math]\displaystyle{ \mathrm{cov}(Y_1,Y_2) = \sum\limits_{i=1}^n\sum\limits_{j=1}^m a_i b_j \mathrm{cov}(X_i,X_j) }[/math].

В частности, ковариация (в отличие от коэффициента корреляции) не инвариантна относительно смены масштаба, что не всегда удобно в приложениях.

• Если [math]\displaystyle{ \alpha }[/math] и [math]\displaystyle{ \beta }[/math] — числа, то

  [math]\displaystyle{ \mathrm{cov}(X+\alpha,Y+\beta) = \mathrm{cov}(X,Y) }[/math].

• Неравенство Коши — Буняковского: если принять в качестве скалярного произведения двух случайных величин ковариацию [math]\displaystyle{ \langle X, Y \rangle = \mathrm{cov}(X, Y) }[/math], то квадрат нормы случайной величины будет равен дисперсии [math]\displaystyle{ \|X\|^2 = \mathrm{D}[X] }[/math], и неравенство Коши — Буняковского запишется в виде:

  [math]\displaystyle{ \mathrm{cov}^2(X,Y) \leqslant \mathrm{D}[X] \cdot \mathrm{D}[Y] }[/math].

Коэффициент корреляции

Коэффициент корреляции r или R- мера линейной зависимости между двумя случайными величинами. R лежит в пределах от -1 до 1. Если ковариация положительна, то с ростом значений одной случайной величины, значения второй имеют тенденцию возрастать, а если знак отрицательный — то убывать.

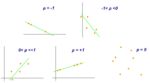
По абсолютному значению ковариации нельзя судить о том, насколько сильно величины взаимосвязаны, так как масштаб ковариации зависит от их дисперсий. Значение ковариации можно нормировать, поделив её на произведение среднеквадратических отклонений (квадратных корней из дисперсий) случайных величин. Полученная величина называется коэффициентом корреляции Пирсона [math]\displaystyle{ \mathbf{r}(X,Y) }[/math], который всегда находится в интервале от −1 до 1:

[math]\displaystyle{ \mathbf{r}(X,Y) = \frac{\mathrm{cov}(X,Y)}{\sigma_X\sigma_Y} }[/math], где [math]\displaystyle{ \sigma }[/math] — среднеквадратическое отклонение.

Соответственно,

[math]\displaystyle{ \mathrm{cov}(X,Y) = \mathbf r(X,Y)\cdot\sigma_X\sigma_Y }[/math].

Случайные величины, имеющие нулевую ковариацию, называются некоррелированными. Независимые случайные величины всегда некоррелированы. Обратное утверждение не всегда выполняется. Оно справедливо для нормально распределенных случайных величин.

См. также

• Ковариационная матрица — обобщение понятия ковариации для векторов из случайных величин
• Корреляция
• Дисперсия случайной величины

Ссылки

• Weisstein, Eric W. Covariance (англ.) на сайте Wolfram MathWorld.