Конечные разности

Конечная разность — математический термин, широко применяющийся в методах вычисления при интерполировании и численном дифференцировании.

Определение

Три типа конечных разностей.

Пусть для некоторой точки [math]\displaystyle{ x_0 }[/math] задано [math]\displaystyle{ n+1 }[/math] узлов интерполяции [math]\displaystyle{ x_k = x_0 + hk, \; k = 0,\ldots,n }[/math] с шагом [math]\displaystyle{ h=\mathrm{const} }[/math] и известны значения функции [math]\displaystyle{ f }[/math] в этих узлах:

[math]\displaystyle{ f(x_0) = y_0, \ldots, f(x_n)=y_n. }[/math]

Тогда восходящей конечной разностью (или разностью вперёд) 1-го порядка называют разность между [math]\displaystyle{ (k+1) }[/math]-м и [math]\displaystyle{ k }[/math]-м значениями [math]\displaystyle{ f }[/math] в узлах интерполяции, то есть

[math]\displaystyle{ \Delta y_k=y_{k+1}-y_k = f(x_{k+1}) - f(x_k),\ k=0,\ldots,n-1. }[/math]

Нисходящей конечной разностью (или разностью назад) 1-го порядка называют разность между [math]\displaystyle{ k }[/math]-м и [math]\displaystyle{ (k-1) }[/math]-м значениями [math]\displaystyle{ f }[/math] в узлах интерполяции, то есть

[math]\displaystyle{ \nabla y_k=y_k - y_{k-1} = f(x_k) - f(x_{k-1}),\ k=1,\ldots,n. }[/math]

Центральной (или симметричной) конечной разностью 1-го порядка называют разность между [math]\displaystyle{ (k+1) }[/math]-м и [math]\displaystyle{ (k-1) }[/math]-м значениями [math]\displaystyle{ f }[/math] в узлах интерполяции, то есть

[math]\displaystyle{ \delta \, y_k=y_{k+1}-y_{k-1} = f(x_{k+1}) - f(x_{k-1}),\ k=1,\ldots,n-1. }[/math]

Разности высших порядков

Восходящей конечной разностью 2-го порядка называют разность между [math]\displaystyle{ (k+1) }[/math]-ой и [math]\displaystyle{ k }[/math]-ой конечными разностями 1-го порядка, то есть

[math]\displaystyle{ \Delta^2y_k= \Delta(\Delta y_k) = \Delta y_{k+1} - \Delta y_k = f(x_{k+2}) - 2 f(x_{k+1}) + f(x_{k}),\ k=0,\ldots,n-2. }[/math]

Соответственно, восходящей конечной разностью порядка [math]\displaystyle{ m }[/math] (для [math]\displaystyle{ m \leq n }[/math]) называют разность между [math]\displaystyle{ (k+1) }[/math]-ой и [math]\displaystyle{ k }[/math]-ой конечными разностями порядка [math]\displaystyle{ m-1 }[/math], то есть

[math]\displaystyle{ \Delta^my_k= \Delta(\Delta^{m-1} y_k) = \Delta^{m-1}y_{k+1} - \Delta^{m-1}y_k,\ k=0,\ldots,n-m. }[/math]

Аналогично определяются нисходящие и центральные разности высших порядков:

[math]\displaystyle{ \nabla^m y_k = \nabla(\nabla^{m-1} y_k), }[/math]

[math]\displaystyle{ \delta^m y_k = \delta(\delta^{m-1} y_k). }[/math]

Через операторы

Если ввести оператор смещения [math]\displaystyle{ \operatorname{E} }[/math] такой, что [math]\displaystyle{ \operatorname{E}y_k=y_{k+1} }[/math], то можно определить оператор восходящей конечной разности [math]\displaystyle{ \Delta }[/math] как [math]\displaystyle{ \operatorname{E}-1 }[/math]. Для него справедливо соотношение

[math]\displaystyle{ \Delta^k=(\operatorname{E}-1)^k }[/math],

которое можно раскладывать по биному Ньютона. Данный способ представления [math]\displaystyle{ \Delta }[/math] заметно упрощает работу с конечными разностями высших порядков.

Общие формулы

Часто также используется другое обозначение: [math]\displaystyle{ \Delta^m_h (f, x) }[/math] — восходящая конечная разность порядка [math]\displaystyle{ m }[/math] от функции [math]\displaystyle{ f }[/math] c шагом [math]\displaystyle{ h }[/math], взятая в точке [math]\displaystyle{ x }[/math]. Например, [math]\displaystyle{ \Delta^1_h (f, x) = f(x+h) - f(x) }[/math]. Аналогично, для нисходящих разностей можно использовать обозначение [math]\displaystyle{ \nabla^m_h (f, x) }[/math], а для центральных — [math]\displaystyle{ \delta^m_h (f, x) }[/math].

В этих обозначениях можно записать общие формулы для всех видов конечных разностей произвольного порядка с использованием биномиальных коэффициентов:

[math]\displaystyle{ \Delta^m_h(f,x) = \sum_{i = 0}^{m} (-1)^{m-i} C_m^i f\bigl(x + i h\bigr), }[/math]

[math]\displaystyle{ \nabla^m_h(f,x) = \sum_{i = 0}^{m} (-1)^i C_m^i f(x - ih), }[/math]

[math]\displaystyle{ \delta^m_h(f,x) = \sum_{i = 0}^{m} (-1)^i C_m^i f\left(x + \left(\frac{m}{2} - i\right) h\right). }[/math]

Общая формула для [math]\displaystyle{ \Delta^m_h(f,x) }[/math] используется при построении интерполяционного многочлена Ньютона.

Пример

Пример вычисления конечных разностей

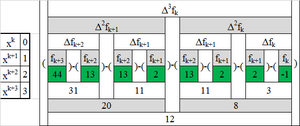
На приведённом изображении рассмотрен пример вычисления конечных разностей для

[math]\displaystyle{ \begin{array}{rcl} f(x) &= &2x^3 - 2x^2 + 3x - 1, \\ x_0 &= &0, \\ n &= &3, \\ h &= &1. \end{array} }[/math]

В зелёных клетках расположены значения [math]\displaystyle{ y_0,\ldots,y_n }[/math], в каждой последующей строке приводятся конечные разности соответствующего порядка.

Связь с производными

Производная функции [math]\displaystyle{ f }[/math] в точке [math]\displaystyle{ x }[/math] определяется с помощью предела:

[math]\displaystyle{ f'(x) = \lim_{h\to0} \frac{f(x+h) - f(x)}{h}. }[/math]

Под знаком предела стоит восходящая конечная разность [math]\displaystyle{ \Delta_h^1(f,x) }[/math], делённая на шаг. Следовательно, эта дробь аппроксимирует производную при малых значениях шага. Погрешность приближения может быть получена с использованием формулы Тейлора:

[math]\displaystyle{ \frac{\Delta_h^1(f,x)}{h} - f'(x) = O(h)\to 0, \; h \to 0. }[/math]

Аналогичное соотношение выполняется для нисходящей разности:

[math]\displaystyle{ \frac{\nabla_h^1(f,x)}{h} - f'(x) = O(h)\to 0, \; h \to 0. }[/math]

Центральная разность даёт более точное приближение:

[math]\displaystyle{ \frac{\delta_h^1(f,x)}{h} - f'(x) = O\left(h^2\right), \; h \to 0. }[/math]

Конечные разности порядка [math]\displaystyle{ m }[/math], делённые на шаг, возведённый в степень [math]\displaystyle{ m }[/math], аппроксимируют производную порядка [math]\displaystyle{ m }[/math]. Порядок погрешности приближения при этом не меняется:

[math]\displaystyle{ \frac{d^m f}{d x^m}(x) = \frac{\Delta_h^m(f,x)}{h^m}+O(h) = \frac{\nabla_h^m(f,x)}{h^m}+O(h) = \frac{\delta_h^m(f,x)}{h^m} + O\left(h^2\right). }[/math]

Связанные понятия

Видно, что конечная разность при фиксированном шаге есть линейный оператор, отображающий пространство непрерывных функций в себя. Обобщением понятия конечной разности является понятие разностного оператора.

С конечными разностями также связаны понятия разделённых разностей и модуля непрерывности.

Литература

• Бахвалов, Н. С., Жидков, Н. П., Кобельков, Г. М. Численные методы . — 7-е изд.. — М.: БИНОМ. Лаборатория знаний, 2011. — 636 с. — ISBN 978-5-9963-0449-3.
• Корн Г. А., Корн Т. М. Справочник по математике для научных работников и инженеров. — М.: «Наука», 1974.

См. также

• Коэффициенты формул численного дифференцирования
• Линейная рекуррентная последовательность — решение наиболее простого типа разностного уравнения
• Метод конечных разностей
• Интерполяционные формулы Ньютона
• Разделенная разность
• Биномиальные преобразования