Ингибирование ферментов

Рис. 1: Общая схема ингибирования фермента

Ферментативный ингибитор — вещество, замедляющее протекание ферментативной реакции. Различают обратимые и необратимые ингибиторы (см. ниже).

Изучение ингибирования ферментов играет важную роль в создании лекарств, в изучении механизма действия и структуры ферментов.

Обратимое ингибирование

Конкурентное ингибирование

Рис. 2: Конкурентное ингибирование при различных концентрациях ингибитора в двойных обратных координатах ( 1 ... [I]=0, 2 ... [I]>0, 3 ... [I]>[I]2)

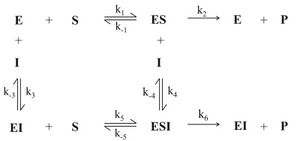
В этом случае ингибитор связывается в активном центре фермента и конкурирует за него с субстратом. Таким образом, конкурентный ингибитор не связывается с фермент-субстратным комплексом (ES на рис.1), то есть константа диссоциации K_i' >> 1.

Конкурентный ингибитор обычно структурно схож с субстратом, однако фермент не способен катализировать реакцию в присутствии ингибитора из-за отсутствия у последнего необходимых функциональных групп.

Схема конкурентного ингибирования и уравнение Михаэлиса-Ментен для него выглядят следующим образом:

[math]\displaystyle{ E+S \longrightarrow ES \longrightarrow E+P }[/math] [math]\displaystyle{ +I \downarrow \uparrow }[/math]      [math]\displaystyle{ EI }[/math]

[math]\displaystyle{ v_0=\frac{V_{max}[S]}{[S]+K_m(1+\frac{[I]}{K_i})} }[/math]

Видно, что при конкурентном ингибировании максимальная скорость реакции V_max не меняется, а кажущаяся константа Михаэлиса увеличивается в (1 + [I]/K_i) раз. Поэтому в двойных обратных координатах Лайнуивера-Берка (зависимость 1/v₀ от 1/[S]) при разных концентрациях ингибитора получают семейство прямых с различным наклоном, пересекающихся в одной точке на оси ординат.

Константу ингибирования K_i обычно определяют так: проводят ряд измерений кажущейся константы Михаэлиса при различных концентрациях ингибитора, затем строят зависимость этой величины от концентрации ингибитора. Тангенс угла наклона полученной прямой равен K_m/K_i.

Неконкурентное ингибирование

Рис. 3: Неконкурентное ингибирование в двойных обратных координатах при различных концентрациях ингибитора ( 1 ... [I]=0, 2 ... [I]>0, 3 ... [I]>[I]2)

Неконкурентный ингибитор не мешает связыванию субстрата с ферментом. Он способен присоединяться как к свободному ферменту, так и к фермент-субстратному комплексу с одинаковой эффективностью. Ингибитор вызывает такие конформационные изменения, которые не позволяют ферменту превращать субстрат в продукт, но не влияют на сродство фермента к субстрату.

Схема и уравнение Михаэлиса-Ментен в случае неконкурентного ингибирования:

[math]\displaystyle{ E+S \longrightarrow ES \longrightarrow E+P }[/math] [math]\displaystyle{ +I \downarrow \uparrow ~~ ~~ ~~ ~~ ~~ \uparrow \downarrow +I }[/math]       [math]\displaystyle{ EI ~~ ~\leftrightarrow ~~ ESI }[/math]

[math]\displaystyle{ v_0=\frac{\frac{V_{max}}{(1+\frac{[I]}{K_i})}[S]}{[S]+K_m} }[/math]

При неконкурентном ингибировании константа Михаэлиса не изменяется, а максимальная скорость реакции уменьшается в (1 + [I]/K_i) раз. Поэтому в двойных обратных координатах семейство прямых, отвечающих разным концентрациям ингибитора, пересекается в одной точке на оси абсцисс.

Бесконкурентное ингибирование

При бесконкурентном ингибировании ингибитор связывается только с фермент-субстратным комплексом, но не со свободным ферментом. Субстрат, связываясь с ферментом, изменяет его конформацию, что делает возможным связывание с ингибитором. Ингибитор, в свою очередь, так меняет конформацию фермента, что катализ становится невозможным.

Схема и уравнение Михаэлиса-Ментен в случае бесконкурентного ингибирования:

[math]\displaystyle{ E+S \longrightarrow ES \longrightarrow E+P }[/math] [math]\displaystyle{ +I \downarrow \uparrow }[/math] [math]\displaystyle{ ESI }[/math]

[math]\displaystyle{ v_0=\frac{\frac{V_{max}}{(1+\frac{[I]}{K_I})}[S]}{[S]+\frac{K_m}{(1+\frac{[I]}{K_I})}} }[/math]

Максимальная скорость реакции и кажущаяся константа Михаэлиса уменьшаются в одинаковое число раз. Поэтому в двойных обратных координатах для разных концентраций ингибитора получаем семейство параллельных прямых.

Ингибирование субстратом

Ингибирование субстратом — частный случай бесконкурентного ингибирования, когда две молекулы субстрата связываются с ферментом, что препятствует образованию продукта.

Схема и уравнение Михаэлиса-Ментен в случае ингибирования субстратом:

[math]\displaystyle{ E+S \longrightarrow ES \longrightarrow E+P }[/math] [math]\displaystyle{ +S \downarrow \uparrow }[/math] [math]\displaystyle{ ESS }[/math]

[math]\displaystyle{ v_0=\frac{V_{max}[S]}{[S]+K_m+\frac{[S]^2}{K_I}} }[/math]

Необратимое ингибирование

Формирование стабильного комплекса ингибитора с ферментом, ведущее к его необратимой инактивации. Случай необратимого ингибирования можно обнаружить по тому признаку, что при разбавлении раствора не происходит повышения удельной активности фермента, как в случае обратимого ингибирования

Рис. 4: Структура активного центра трипантионредуктазы с двумя молекулами ингибиторов, один из которых связан необратимо, а другой обратимо. Фермент показан синим цветом. Изображение создано на основе PDB 1GXF.

Аллостерическое ингибирование

Аллостерические ингибиторы связываются с отдельными участками фермента вне активного центра. Такое связывание влечет за собой конформационные изменения в молекуле фермента, которые приводят к уменьшению его активности. Аллостерические эффекты встречаются практически только в случае олигомерных ферментов. Кинетику таких систем нельзя описать с помощью простой модели Михаэлиса-Ментен.

Ссылки

• Лекция по ферментативному катализу на кафедре химической энзимологии химического факультета МГУ
• Курс по биохимии Университета Калифорнии
• Основная справочная информация и механизмы действия ингибиторов
• Вопросы-ответы. Технические рекомендации по работе с ингибиторами