Перейти к содержанию

Задача синхронизации стрелков

Эта статья находится на начальном уровне проработки, в одной из её версий выборочно используется текст из источника, распространяемого под свободной лицензией
Материал из энциклопедии Руниверсалис
Неполное решение[1]: [math]\displaystyle{ 2^m }[/math] роботов с 4 состояниями синхронизируются за [math]\displaystyle{ 2^m - 1 }[/math] тактов (на такт дольше оптимума). Видна волна сигналов, прошедшая через весь строй и отразившаяся обратно. Сигнал к выстрелу — у тебя флаг, у соседей ружьё (или наоборот).

Зада́ча синхрониза́ции стрелко́в — задача из области информатики и теории клеточных автоматов.

Впервые предложенная Джоном Майхиллом в 1957 году и опубликованная (с решением) в 1962 году Эдвардом Муром[2]. Название связано с поведением солдат при расстреле или ружейном салюте — все солдаты стреляют одновременно по сигналу.

Формулируется следующим образом: можно ли так запрограммировать одномерный клеточный автомат конечной длины, чтобы из стартового состояния G●●…●●● все клетки одновременно перешли в состояние FFF…FFF, независимо от длины цепочки, если обязательно правило перехода ●●●→● и его аналоги для концов цепочки ⌀●●→●, ●●⌀→●? Простым языком[3]:

  • [math]\displaystyle{ n \geqslant 2 }[/math] роботов (конечных автоматов) с ружьями стоят шеренгой. У автоматов как минимум три состояния ●, G и F — «исходное», «командир» и «выстрел». Помимо этих трёх, можно добавить сколько угодно промежуточных состояний.
  • Роботы действуют независимо по одной программе и общаются только по цепочке: по сигналам барабана (синхронизатора) в зависимости от своего состояния в момент [math]\displaystyle{ t - 1 }[/math] и состояния двух соседей переходят в новое состояние. Исключение — крайние роботы, у которых только один сосед; у них собственные программы.
  • Все три программы, если робот и его соседи в исходном состоянии, ничего не должны делать.
  • Все роботы стоят в исходном состоянии и ничего не делают. В момент [math]\displaystyle{ t=0 }[/math] крайнего левого переводят в состояние «командир».
  • Существуют ли такие три программы (набор состояний и три комплекта правил перехода — для командира, замыкающего и остальных роботов), чтобы при любом [math]\displaystyle{ n }[/math] они одновременно (на одном ударе барабана) перешли в состояние «выстрел»?

Поскольку сигнал распространяется по шеренге со скоростью 1 позиция за такт (в теории клеточных автоматов это называется «скорость света»), очевидно, время синхронизации будет возрастать с возрастанием [math]\displaystyle{ n }[/math].

История

Одно из решений задачи с использованием 15 состояний у каждого стрелка и [math]\displaystyle{ 3n }[/math] единиц времени. Время нарастает сверху вниз.
Решение продолжительностью [math]\displaystyle{ 2n-2 }[/math] единиц времени. Время нарастает сверху вниз.
Открытая математическая проблема

Существует ли решение задачи синхронизации стрелков в пять состояний — для любого [math]\displaystyle{ n }[/math], не обязательно оптимальное по времени?

Первое решение этой задачи было найдено Джоном Маккарти и Марвином Мински и было опубликовано в Sequential Machines Эдвардом Муром.

Решение, требующее минимальное время, было найдено в 1962 профессором Эйити Гото из МТИ[4]. Оно использует несколько тысяч состояний и требует ровно [math]\displaystyle{ 2 n - 2 }[/math] единиц времени для [math]\displaystyle{ n }[/math] роботов. Легко доказывается (см. ниже), что более эффективных по времени решений не существует.

Оптимальное решение, использующее всего шесть состояний (включая конечное «выстрел»), было найдено Жаком Мазойером в 1987 году[5]. Ранее Роберт Бальцер компьютерным перебором доказал, что решений с четырьмя состояниями клеток не существует[6]. Питер Сандерс позднее выяснил, что поисковая процедура Бальцера была неполной, однако исправив процедуру, получил тот же результат. В 2010-е эволюционным перебором получены сотни разных решений с шестью состояниями[7]. До сих пор неизвестно, существует ли решение с пятью состояниями клеток.

Также пытаются побить рекорд по количеству задействованных правил перехода (включая требуемое, но неиспользуемое правило для командира ⌀●●→●[7]. В решении Мазойера 119 правил. Существует неоптимальное по времени решение с шестью состояниями и 78-ю правилами, и оптимальное — с 80-ю.

Находят неполные решения с четырьмя состояниями — например, синхронизирующие шеренгу из [math]\displaystyle{ 2^m }[/math] роботов[1].

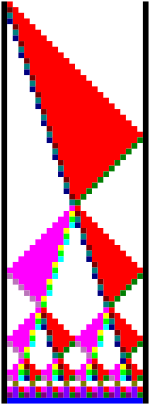
Простейшее решение

Простейшее решение задачи описывает две волны состояний, распространяющиеся по шеренге роботов, одна из которых движется в три раза быстрее другой. Быстрая волна отражается от дальнего края ряда и встречается с медленной в центре. После этого две волны разделяются на четыре, движущиеся в разные стороны от центра. Процесс продолжается, каждый раз удваивая число волн, пока длина отрезков ряда не станет равной 1. В этот момент все роботы стреляют. Это решение требует [math]\displaystyle{ 3n }[/math] единиц времени для [math]\displaystyle{ n }[/math] солдат.

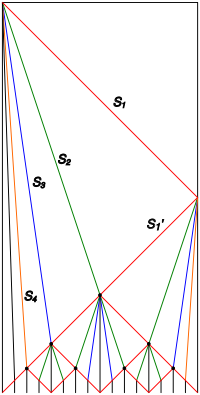
Решение, требующее минимального времени

Здесь описано достаточно простое решение из 16 состояний, описанное Абрахамом Ваксманом в 1966 году[8]. Командир посылает соседнему роботу сигналы [math]\displaystyle{ S_1,~~S_2,~~S_3~~ \dots ~~ S_i \dots }[/math] с частотами [math]\displaystyle{ 1,~ \frac {1}{3},~ \frac {1} {7},~ \dots~ \frac {1} {2^{i - 1} - 1}\dots }[/math] Сигнал [math]\displaystyle{ S_1 }[/math] отражается от правого края ряда и встречает сигнал [math]\displaystyle{ S_i }[/math] (для [math]\displaystyle{ i \ge 2 }[/math]) в ячейке [math]\displaystyle{ n/2^{i - 1}. }[/math] Когда [math]\displaystyle{ S_1 }[/math] отражается, он также создает нового командира на правом конце.

Сигналы [math]\displaystyle{ S_i }[/math] генерируются с использованием вспомогательных сигналов, распространяющихся влево. Каждый второй момент времени обычный сигнал генерирует вспомогательный сигнал, распространяющийся влево. [math]\displaystyle{ S_1 }[/math] движется самостоятельно со скоростью 1, тогда как более медленные сигналы движутся только при получении вспомогательных сигналов.

Доказательство минимального времени

Если между командиром (инициатором стрельбы) и ближайшим концом [math]\displaystyle{ k }[/math] роботов, на синхронизацию нужно не менее [math]\displaystyle{ 2n-2-k }[/math] шагов[9].

Частный случай: если командир на краю — то [math]\displaystyle{ 2n - 2 }[/math] шага.

Доказательство. Допустим, существует тройка программ, которая решает задачу синхронизации, и для некоторых [math]\displaystyle{ n }[/math] и [math]\displaystyle{ k }[/math] сумеет выстрелить за [math]\displaystyle{ t \lt 2n - 2 - k }[/math]. Считаем, что командир ближе к левому концу.

Любой сигнал проходит от робота к роботу не быстрее, чем с так называемой «скоростью света» — 1 позиция за шаг времени. Действия первого робота в момент [math]\displaystyle{ t }[/math] зависят от первых двух роботов на момент [math]\displaystyle{ t - 1 }[/math], от первых трёх на момент [math]\displaystyle{ t - 2 }[/math], …, от всех [math]\displaystyle{ n }[/math] роботов на момент [math]\displaystyle{ t_1 = t - (n - 1) \leqslant n - 2 - k }[/math]. В этот момент последний робот всё ещё в исходном состоянии (сигнал к нему приходит к моменту [math]\displaystyle{ n - 1 - k }[/math]).

А значит, если добавить к правому концу ещё [math]\displaystyle{ (n+2) }[/math]-х роботов, в момент [math]\displaystyle{ t_1 }[/math] состояние первых [math]\displaystyle{ n }[/math] роботов будет таким же, для первого робота ничего не изменится, и он выстрелит на том же шаге [math]\displaystyle{ t }[/math]. Последний [math]\displaystyle{ (2n+2) }[/math]-й на шаге [math]\displaystyle{ t }[/math] останется в исходном состоянии — до него сигнал не успеет дойти. Так что данная тройка программ — не решение. Противоречие.

Точно так же доказывается и другая нижняя грань, [math]\displaystyle{ n - 1 + k }[/math] шагов, но число [math]\displaystyle{ 2n-2-k }[/math] не меньше.

Примечание. Дополнительные требования к [math]\displaystyle{ n }[/math] и [math]\displaystyle{ k }[/math], если [math]\displaystyle{ n }[/math] не ограничено сверху, могут дать выигрыш по количеству состояний, но не по времени, и действительно существует обобщение решения Ваксмана из 17 состояний, работающее для любых [math]\displaystyle{ n }[/math] и [math]\displaystyle{ k }[/math] за [math]\displaystyle{ 2n-2-k }[/math] шагов[10].

Обобщения

Было предложено и изучено несколько более общих формулировок задачи, включая ряды с произвольным расположением командира, замкнутые кольца, квадраты, кубы, графы Кэли и графы общего вида.

Если от знания, что командир находится на краю линейного строя, не удаётся выиграть во времени синхронизации, то в двухмерном строю от знания, что он квадратный, будет выигрыш[11].

Удалось найти существование решения для линейного строя, если каждый робот должен дать сигнал за [math]\displaystyle{ \tau_i }[/math] тактов до выстрела, робот знает максимальное и своё [math]\displaystyle{ \tau_i }[/math], и соответственно программируется[12]. Простейшее решение — дать роботам [math]\displaystyle{ \max\tau_i }[/math] дополнительных состояний и столько же тактов на синхронизацию, но можно обойтись и без этой задержки, если строй достаточно длинный. Сложность каждой отдельной программы [math]\displaystyle{ a^{2\max\tau_i + 1} }[/math] (по сути, он помнит состояние [math]\displaystyle{ 2\max\tau_i + 1 }[/math] робота из классической задачи).

Точное минимальное время синхронизации на разных строях
(найдено решение и доказано, что быстрее не бывает)
Форма строя Минимальное время
Шеренга, между командиром и ближним краем [math]\displaystyle{ k }[/math] роботов [math]\displaystyle{ 2n-2-k }[/math][9]
Кольцо [math]\displaystyle{ n-1 }[/math][9]
Кольцо с односторонним распространением информации [math]\displaystyle{ 2n-2 }[/math][9]
Каре [math]\displaystyle{ m \times n }[/math] с командиром на углу [math]\displaystyle{ m + n + \operatorname{max}\{m,n\} - 3 }[/math][11]
Квадрат [math]\displaystyle{ n \times n }[/math] с командиром на углу [math]\displaystyle{ 2n - 2 }[/math][11]
Куб [math]\displaystyle{ n \times n \times n }[/math] с командиром в вершине [math]\displaystyle{ 3n - 3 }[/math][11]

Примечания

  1. ↑ Перейти обратно: 1,0 1,1 https://www.researchgate.net/publication/220977377_About_4-States_Solutions_to_the_Firing_Squad_Synchronization_Problem
  2. ↑ F. R. Moore, G. G. Langdon, A generalized firing squad problem. Information and Control, Volume 12, Issue 3, March 1968, Pages 212—220. DOI
  3. ↑ [Confetti] Firing Squad synchronization problem — YouTube
  4. ↑ Goto E. A minimal time solution of the firing squad problem. Dittoed course notes for Applied Mathematics, vol.298,pp.52-59. Harvard University, Cambridge(1962)
  5. ↑ Jacques Mazoyer, A six-state minimal time solution to the firing squad synchronization problem. Theoretical Computer Science, 1987, vol. 50 pp 183—238 DOI
  6. ↑ Robert Balzer, An 8-state Minimal Time Solution to the Firing Squad Synchronization Problem. Information and Control, 1967, vol.10, pp.22—42 DOI
  7. ↑ Перейти обратно: 7,0 7,1 Accueil — Archive ouverte HAL
  8. ↑ Abraham Waksman, An Optimum Solution to the Firing Squad Synchronization Problem. Information and Control, 1966, vol.9, pp.66—78 DOI
  9. ↑ Перейти обратно: 9,0 9,1 9,2 9,3 The Firing Squad Problem
  10. ↑ https://www.sciencedirect.com/science/article/pii/S0019995868903094
  11. ↑ Перейти обратно: 11,0 11,1 11,2 11,3 Shinahr, Ilka. Two- and three-dimensional firing-squad synchronization problem (англ.) // Information and Control[англ.] : journal. — Academic Press, 1974. — Vol. 24. — P. 163—180. — doi:10.1016/S0019-9958(74)80055-0.
  12. ↑ В. И. Варшавский, В. Б. Мараховский, В. А. Песчанский, «Некоторые варианты задачи о синхронизации цепи автоматов», Пробл. передачи информ., 4:3 (1968), 73-83; Problems Inform….

Литература

Ссылки

Источник — https://xn--h1ajim.xn--p1ai/index.php?title=Задача_синхронизации_стрелков&oldid=5861323