Дифракция на N щелях

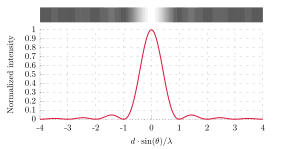
Дифракция на двух щелях красного лазера

Дифракция на двух и пяти щелях

Распространение волны через щель шириною в длину волны.

Распространение волны через щель, превосходящую шириною длину волны в шесть раз.

Численное приближение дифракционной картины для щели шириной в четыре длины волны с падающей плоской волной. Видны центральный луч, нули, изменение фазы на [math]\displaystyle{ \pi }[/math].

График и вид дифракции на одной щели.

Дифракция на N щелях — это частная задача оптики, где рассматривается дифракция на нескольких щелях в непроницаемом экране.

Рассмотрим сначала математическое представление принципа Гюйгенса:

[math]\displaystyle{ \Psi = \int_{slit} \frac{i}{r\lambda} \Psi^\prime e^{-ikr}\,dslit }[/math]

Рассмотрим N щелей в экране с равными ширинами (a, [math]\displaystyle{ \infty }[/math], 0) и расстояниями d между ними вдоль оси x′. Расстояние r от первой щели задаётся формулой:

[math]\displaystyle{ r = z \left(1 + \frac{\left(x - x^\prime\right)^2 + y^{\prime2}}{z^2}\right)^\frac{1}{2} }[/math]

Для обобщения на N щелей, заметим, что z и y остаются постоянными, когда x′ сдвигается на

[math]\displaystyle{ x_{j=0 \cdots n-1}^{\prime} = x_0^\prime - j d }[/math]

Таким образом,

[math]\displaystyle{ r_j = z \left(1 + \frac{\left(x - x^\prime - j d \right)^2 + y^{\prime2}}{z^2}\right)^\frac{1}{2} }[/math]

и сумма по всем N вкладам в амплитуду:

[math]\displaystyle{ \Psi = \sum_{j=0}^{N-1} C \int_{-\frac{a}{2}}^{\frac{a}{2}} e^\frac{ikx\left(x^\prime - jd\right)}{z} e^\frac{-ik\left(x^\prime - jd\right)^2}{2z} \,dx^\prime }[/math]

Замечая, что величина [math]\displaystyle{ \frac{k\left(x^\prime -jd\right)^2}{z} }[/math] мала при рассмотрении дифракции Фраунгофера, и [math]\displaystyle{ e^\frac{-ik\left(x^\prime -jd\right)^2}{2z} \approx 1 }[/math], получим:

[math]\displaystyle{ \Psi }[/math]	[math]\displaystyle{ = C\sum_{j=0}^{N-1} \int_{-\frac{a}{2}}^{\frac{a}{2}} e^\frac{ikx\left(x^\prime - jd\right)}{z} \,dx^\prime }[/math]
	[math]\displaystyle{ = C \sum_{j=0}^{N-1} \frac{\left(e^{\frac{ikax}{2z} - \frac{ijkxd}{z}} - e^{\frac{-ikax}{2z}-\frac{ijkxd}{z}}\right)}{\frac{2ikax}{2z}} }[/math]
	[math]\displaystyle{ = C \sum_{j=0}^{N-1} e^\frac{ijkxd}{z} \frac{\left(e^\frac{ikax}{2z} - e^\frac{-ikax}{2z}\right)}{\frac{2ikax}{2z}} }[/math]
	[math]\displaystyle{ = C \frac{\sin\frac{ka\sin\theta}{2}}{\frac{ka\sin\theta}{2}} \sum_{j=1}^{N-1} e^{ijkd\sin\theta} }[/math]

Теперь используем следующее равенство:

[math]\displaystyle{ \sum_{j=0}^{N-1} e^{x j} = \frac{1 - e^{Nx}}{1 - e^x}. }[/math]

Подставляя в наше уравнение, приходим к выражению:

[math]\displaystyle{ \Psi }[/math]	[math]\displaystyle{ = C \frac{\sin\frac{ka\sin\theta}{2}}{\frac{ka\sin\theta}{2}}\left(\frac{1 - e^{iNkd\sin\theta}}{1 - e^{ikd\sin\theta}}\right) }[/math]
	[math]\displaystyle{ = C \frac{\sin\frac{ka\sin\theta}{2}}{\frac{ka\sin\theta}{2}}\left(\frac{e^{-iNkd\frac{\sin\theta}{2}}-e^{iNkd\frac{\sin\theta}{2}}}{e^{-ikd\frac{\sin\theta}{2}}-e^{ikd\frac{\sin\theta}{2}}}\right)\left(\frac{e^{iNkd\frac{\sin\theta}{2}}}{e^{ikd\frac{\sin\theta}{2}}}\right) }[/math]
	[math]\displaystyle{ = C \frac{\sin\frac{ka\sin\theta}{2}}{\frac{ka\sin\theta}{2}}\frac{\frac{e^{-iNkd \frac{\sin\theta}{2}} - e^{iNkd\frac{\sin\theta}{2}}}{2i}}{\frac{e^{-ikd\frac{\sin\theta}{2}} - e^{ikd\frac{\sin\theta}{2}}}{2i}} \left(e^{i(N-1)kd\frac{\sin\theta}{2}}\right) }[/math]
	[math]\displaystyle{ = C \frac{\sin\left(\frac{ka\sin\theta}{2}\right)}{\frac{ka\sin\theta}{2}} \frac{\sin\left(\frac{Nkd\sin\theta}{2}\right)} {\sin\left(\frac{kd\sin\theta}{2}\right)}e^{i\left(N-1\right)kd\frac{\sin\theta}{2}} }[/math]

поставим k в виде [math]\displaystyle{ \frac{2\pi}{\lambda} }[/math] и представляя все неосциллирующие постоянные как [math]\displaystyle{ I_0 }[/math], как в дифракции на одной щели. Помня [math]\displaystyle{ \langle e^{ix} \Big| e^{ix}\rangle\ = e^0 = 1 }[/math], получим для интенсивности света ответ:

[math]\displaystyle{ I\left(\theta\right) = I_0 \left[ \operatorname{sinc} \left( \frac{\pi a}{\lambda} \sin \theta \right) \right]^2 \cdot \left[\frac{\sin\left(\frac{N\pi d}{\lambda}\sin\theta\right)}{\sin\left(\frac{\pi d}{\lambda}\sin\theta\right)}\right]^2 }[/math]