Асферическая линза

Асфери́ческими называют линзы, одна или обе поверхности которых не являются сферическими.

Асферические поверхности, применяемые в оптике, можно разделить на две основные группы:

1. поверхности вращения, имеющие ось симметрии (аксиально-симметричные);
2. поверхности, обладающие двумя плоскостями симметрии или не имеющие симметрии.

При этом большинство применяющихся в настоящее время асферических поверхностей относятся к первой группе, а из второй группы поверхностей применение находят торические, цилиндрические и некоторые другие типы поверхностей.

Математическое описание

Общее уравнение меридионального сечения асферической поверхности вращения первой группы имеет вид

[math]\displaystyle{ x=A|y|+ By^2+C|y^3|+Dy^4 + ... }[/math]

К тому же большинство применяемых асферических поверхностей обладают параксиальной областью. Для таких поверхностей центральные точки не имеют никаких особенностей (поверхность в этой точке без излома, то есть касательная к поверхности перпендикулярна к её оси). Из поверхностей, не обладающих параксиальной областью, пока применяются только конические.

Наиболее распространены асферические поверхности, в уравнении меридионального профиля которых равны нулю коэффициенты при всех нечетных степенях [math]\displaystyle{ y }[/math]

[math]\displaystyle{ x=By^2 + Dy^4+Fy^6+ ... }[/math]

К таким поверхностям можно отнести все поверхности второго порядка (коникоиды), поверхности коррекционных пластин (например, пластин Шмидта в телескопах одноимённой системы) и др.

Возможности асферических линз по сравнению со сферическим связаны с параметрами, определяющими форму несферических поверхностей. Так, например, меридиональное сечение поверхности вращения 2-го порядка можно выразить уравнением вида

[math]\displaystyle{ y^2=Ax+Bx^2 }[/math]

При этом радиус кривой в её вершине

[math]\displaystyle{ r=A/2 }[/math]

Так как коэффициент B не влияет на радиус, то его изменения (связанные с изменением формы поверхности) не повлияют ни на фокусное расстояние, ни на увеличение системы для параксиального пучка лучей. Таким образом, асферические поверхности 2-го порядка, в отличие от сферических, имеют ещё один расчетный параметр, позволяющий изменять ход краевых лучей, не затрагивая хода лучей параксиальных, что создаёт дополнительные возможности для построения оптических систем.

При оптимизации формы двухсторонней цельной асферической линзы, образованной поверхностями вращения из изотропного оптического материала с показателем преломления большим чем окружающая линзу однородная среда, возникает требование оптимизации: Угол θ₁ падения света в каждой точке проксимальной к точечному источнику поверхности равен углу θ₂ выхода того же луча (прошедшего через преломляющий материал цельной линзы) из дистальной к точечному источнику поверхности. В таком случае для каждого тонкого плоскопараллельного пучка света, условно прошедшего через точечный источник света будут выполняться также условия (см. Схему):

1) Угол ξ₁ преломления луча при падении на проксимальную поверхность цельной линзы равен углу ξ₂ преломления того же луча в точке выхода из дистальной поверхности границы раздела с окружающей средой;

2) Угол η₁ отклонения луча при падении на проксимальную поверхность цельной линзы равен углу η₂ отклонения того же луча в точке выхода из дистальной поверхности границы раздела с окружающей средой;

3) Под тем же лучом понимается здесь группа плоских однородных гармонических волн идущих вдоль линии постоянной амплитуды.

Схема — оптическая диаграмма, показывающая параметры и ход лучей через асферическую линзу

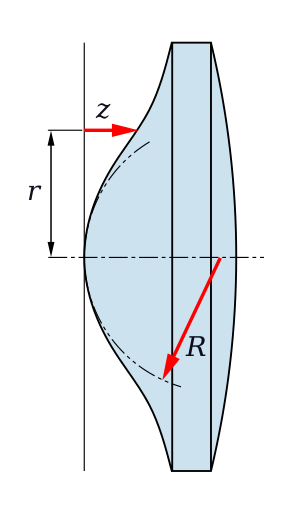
Теперь приведем форму такой линзы (стреловой срез через осевую линию) (см. Схему)

Проксимальная поверхность образована параметрическими уравнениями, соответствующими преобразованиям перехода от полярной системы координат в прямоугольную, где φ, r(φ) — угол и радиус-вектор точки полярной системы координат, показанной на Схеме. Точка O соответствует полюсу полярной системы координат и началу прямоугольной декартовой системы координат.

Уравнения: (Источник [1])

[math]\displaystyle{ x_{1}(\varphi)=r_{1}(\varphi)\cdot \cos(\varphi); }[/math]

[math]\displaystyle{ y_{1}(\varphi)=r_{1}(\varphi)\cdot \sin(\varphi); }[/math]

[math]\displaystyle{ r_{1}(\varphi)=c_{1} \cdot \left ( \frac{1-n}{1-n \cdot \cos (\varphi / 2)} \right )^{2} }[/math],

где с₁ — константа, длина отрезка, который лежит на оси вращения линзы, соединяющего точку O и проксимальную поверхность линзы, причем точка О должна лежать на оси вращения.

[math]\displaystyle{ r_{1}(\varphi) = c_{1} \cdot \left ( \frac{1-n}{1-n \cdot \cos (\varphi / 2)} \right )^{2} }[/math]

[math]\displaystyle{ x_{2}(\varphi)=\frac{(c_{2}-c_{1}) \cdot (n-1) \cdot \cos(\varphi / 2) + r_{1} (\varphi) \cdot (n \cdot \cos(\varphi) - \cos (\varphi / 2) )}{n - \cos (\varphi / 2))} }[/math]

[math]\displaystyle{ y_{2}(\varphi)= \left [ r_{1}(\varphi)+x_{2}(\varphi) \right ] \cdot \tan (\varphi / 2) }[/math],

где с₂ — константа, длина отрезка, который лежит на оси вращения линзы, соединяющего точку O и дистальную поверхность линзы, причем точка O должна лежать на оси вращения; n — показатель преломления материала асферической линзы. При этом вне линзы лучи идут в среде с показателем преломления, равным единице.

Асферическая линза, поверхности вращения которой описаны вышеприведенными уравнениями, имеет свойство преобразовывать излучение расположенного на оси вращения точечного источника в пучок плоских световых волн при прохождении фронта волн в направлении от проксимальной S1 к дистальной S2 поверхности и наоборот, из источника, генерирующего систему плоских волн (отдаленный точечный источник, например Солнце) в фокус O при обратном ходе лучей. Для получения такого идеального геометрического хода лучей нужно устранение или минимизация явления дисперсии показателя преломления материала линзы. Это достигается подбором материала линзы или фильтрами пропускания частот.

Максимальная толщина такой линзы равна:

[math]\displaystyle{ d = \frac{2 \cdot r_{1}(\varphi_{m}) \cdot \sin^{2} (\varphi_{m} / 2) }{n-1} }[/math],

где [math]\displaystyle{ \varphi_{m} }[/math] — угол наибольшего отклонения излучения точечного источника от оси вращения охватываемого линзой. Углы падения θ₁ и выхода θ₂ из поверхностей линзы луча из источника в точке O с угловым отклонением φ от оси вращения:

[math]\displaystyle{ \theta_{1} = \theta_{2} = \arccos \left ( \frac{n \cdot \cos(\varphi/2) - 1}{\sqrt{1+n^2 - 2 \cdot n\cdot \cos(\varphi / 2)}} \right ) }[/math]

Применение

В общем случае, при расчёте оптической системы с заданными аберрациями одна асферическая поверхность может заменить 2 — 3 сферических, что приводит к резкому сокращению числа деталей системы. При этом применение асферических поверхностей, хотя и существенно расширяет возможности разработчика оптических систем, ограничивается сложностью изготовления и контроля, так как типовая технология изготовления сферических поверхностей, основанная на притирании детали и инструмента, неприменима из-за непостоянства кривизны детали.

В современных фотографических объективах широко применяются асферические линзы. При этом было замечено, что применение асферических линз в светосильных объективах в ряде случаях приводит к ухудшению боке, а именно, к формированию характерных концентрических («луковых») колец внутри кругов размытия.

Асферические линзы без осевой симметрии (например цилиндрические) имеют разные фокусные расстояния в разных плоскостях, проходящих через оптическую ось, то есть обладают астигматизмом для осевых пучков лучей. Такие линзы применяются, например, в очках для исправления астигматизма глаза, и в киносъёмочных (кинопроекционных) анаморфотных системах для получения различного масштаба изображения по разным направлениям.

Источники

[1] — Z. Xu, B. Bundschuh*, R. Schwarte, O. Loffeld, F. Klaus, H.Heinol, R. Klein, — Power transmittance of optimized aspherical lens with large numerical aperture, SPIE Vol. 2775, pages 639—646

Литература

• И. Я. Бубис и др., под общ. ред. С. М. Кузнецова и М. А. Окатова, Справочник технолога оптика. Л. «Машиностроение». 1983
• Русинов М. М., Техническая оптика. Л., «Машиностроение», 1979.