Алгоритм HITS

Алгоритм HITS (англ. Hyperlink Induced Topic Search), предложенный в 1999 году Джоном Клейнбергом, позволяет находить Интернет-страницы, соответствующие запросу пользователя, на основе информации, заложенной в гиперссылки[1].
Метрика HITS часто используется для ответа на широкую тему запросов и нахождения сообществ документов(англ. Tightly-Knit Community), в Интернете. Идея алгоритма основана на предположении, что гиперссылки кодируют значительное количество скрытых авторитетных страниц[2].
Авторитетный документ (авторитетная страница, автор) — это документ, соответствующий запросу пользователя, имеющий больший удельный вес среди документов данной тематики, то есть большее число документов ссылаются на данный документ[1].
Хаб-документ (хаб-страница, посредник) — это документ, содержащий много ссылок на авторитетные документы.
Страница, на которую ссылаются многие другие точки должна быть хорошим «автором». В свою очередь страница, которая указывает на многие другие, должна быть хорошим «посредником». Основываясь на этом, в алгоритме HITS для каждой веб-страницы рассчитываются две оценки: оценка авторитетности и посредническая оценка. То есть для каждой страницы рекурсивно вычисляется её значимость как «автора» и «посредника»[3][4].
Алгоритм
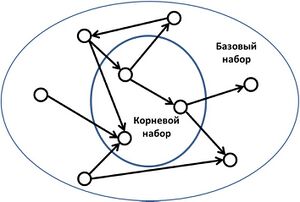
Первым шагом в алгоритме HITS, является получение наиболее релевантных страниц в поисковом запросе. Это множество называется корневым набором и может быть получено путём принятия самых популярных страниц n, возвращаемых текстовым алгоритмом поиска. Базовый набор формируется путём увеличения корневого набора со всеми веб-страницами, которые с ним связаны и с некоторыми страницами, ссылающимися на него. Веб-страницы в базовом наборе и все гиперссылки между этими страниами, образуют сосредоточенный подграф. HITS вычисления выполняются только на этом подграфе.
Оценки авторитетного документа и посредника определены в терминах друг друга во взаимной рекурсии. Оценка авторитетности страницы вычисляется как сумма значений оценок посреднических страниц, которые указывают на эту страницу. Значение оценки посредника вычисляется как сумма оценок авторитетных страниц, на которые он указывает.
Алгоритм выполняет ряд итераций, каждая из которых состоит из двух основных этапов:
- Обновление авторитетности. Обновление авторитетной оценки каждой вершины подграфа, эквивалентное сумме посреднических оценок каждой из вершин, указывающих на них.
- Хаб-обновление. Обновление посреднической оценки каждой вершины подграфа, путём суммирования авторитетных оценок каждой из вершин, на которые они указывают.
Оценка авторитетности и посредническая оценка для вершины рассчитывается по следующему алгоритму:
- Начните с вершин, оценка авторитетности и посредническая оценка которых равна 1.
- Выполнение правила обновления авторитетности.
- Выполнение правила хаб-обновления.
- Нормализация значений путём деления каждой посреднической оценки на корень квадратный из суммы квадратов всех посреднических оценок, и деления каждой оценки авторитетности на корень квадратный из суммы квадратов всех оценок авторитетности.
- Повторение со второго шага по мере необходимости.
Детализация
Чтобы начать ранжирование, [math]\displaystyle{ \forall p }[/math], [math]\displaystyle{ \mathrm{auth}(p) = 1 }[/math] и [math]\displaystyle{ \mathrm{hub}(p) = 1 }[/math]. Рассмотрим два типа обновлений: правило обновления авторитетности и хаб-обновление. Для того чтобы вычислить оценки авторитетности/посредника применяются повторяющиеся итерации правил обновления авторитетности и хаб-обновления. K-шаг применения алгоритма подразумевает под собой применение k-раз первого правила обновления авторитетности и затем правило хаб-обновления.
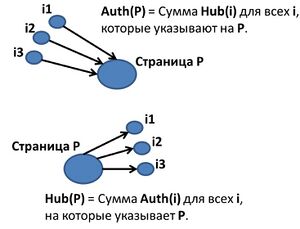
Правило обновления авторитетности
[math]\displaystyle{ \forall p }[/math], мы получаем [math]\displaystyle{ \mathrm{auth}(p) }[/math] = [math]\displaystyle{ \displaystyle\sum_{i=1}^n \mathrm{hub}(i) }[/math] где n — общее количество страниц, связанных с p и i — страница, связанная с p. Таким образом, оценка авторитетности страницы вычисляется как сумма значений оценок посреднических страниц, которые указывают на эту страницу.
Правило хаб-обновления
[math]\displaystyle{ \forall p }[/math], мы получаем [math]\displaystyle{ \mathrm{hub}(p) }[/math] = [math]\displaystyle{ \displaystyle\sum_{i=1}^n \mathrm{auth}(i) }[/math] где n — общее количество страниц, на которые указывает p и i — страница, на которую указывает p. Таким образом, посредническая оценка страницы вычисляется как сумма значений оценок авторитетности страниц, на которых она ссылается.
В зависимости от этих значений рассчитывается важность веб-страниц для конкретного запроса и затем отображается пользователю. Рейтинг модуля HITS вычисляет ранг веб-страницы в автономном режиме после того, как они были загружены и сохранены в локальной базе данных.[5]
Нормализация
Окончательные оценки вершин определяются после бесконечного повторения алгоритма. Прямое и последовательное применение правил хаб-обновления и обновления авторитетности, приводит к расходящимся значениям, которые необходимо нормализовать матрицой после каждой итерации. Таким образом, значения, полученные в результате этого процесса в конечном итоге сходятся.
Алгоритм HITS и PageRank
Алгоритм HITS имеет несколько важных отличий от алгоритма PageRank.[6]
- Алгоритм HITS вычисляет не только ранг каждого узла, но также дает посредническую оценку.
- Алгоритм PageRank содержит свободный параметр α, который обычно не включен в алгоритм HITS.
- Приоритетом, в результате работы алгоритма PageRank, пользуются, как правило, более старшие ресурсы, в то время как HITS алгоритм имеет меньший уклон в этом отношении.
- Алгоритм PageRank может находить единственное уникальное решение.
Несмотря на различия HITS и PageRank, в этих алгоритмах общее то, что авторитетность (вес) узла зависит от веса других узлов, а уровень «посредника» зависит от того, насколько авторитетны узлы, на которые он ссылается.
Расчет авторитетности отдельных документов сегодня широко используется в таких приложениях, как определение порядка сканирования документов в сети роботом ИПС, ранжирование результатов поиска, формирование тематических обзоров и т. п.
В настоящее время приобрели широкое распространение технологии искусственного повышения рангов отдельных веб-документов или их групп веб-сайтов путём установления гиперссылок, не имеющих отношения к их содержанию. Эти технологии, являющиеся неблагонадёжной разновидностью методов поисковой оптимизации SEO (англ. Search Engine Optimization), под названием «чёрное» SEO, основываются на приспособлении к существующим алгоритмам ранжирования веб-документов наиболее популярными (поисковыми системами).
В свою очередь, такие технологии приводят к необходимости постоянного совершенствования алгоритмов ранжирования в поисковых системах, ориентации на содержательную составляющую веб-документов при определении их рангов.[4]
Недостатки HITS
При оценке алгоритма HITS было проведено много исследований и показано, что в то время как алгоритм хорошо работает для большинства запросов, он не работает для некоторых других. Существует несколько причин[7]:
- Посредники и авторы.
Нецелесообразность четкого различия между «посредниками» и «авторами», поскольку многие посреднические страницы также являются и авторскими.
- Сдвиг тематики(англ. Topic drift).
Доминирующее расположение некоторых тематически тесно связанных документов в результате работы алгоритма HITS. В некоторых случаях, эти документы могут быть нерелевантны поставленному запросу. Было зафиксировано, что в одном случае, когда искомым элементом запроса был «Ягуар», алгоритм HITS сходился к футбольной команде под названием Jaguars.
Для решения этой проблемы был предложен алгоритм PHITS[4], как некоторое расширение стандартного алгоритма HITS. В рамках этого алгоритма предполагается: [math]\displaystyle{ D }[/math] — множество цитирующих документов, [math]\displaystyle{ C }[/math] — множество ссылок, [math]\displaystyle{ Z }[/math] — множество классов (факторов). Предполагается также, что событие [math]\displaystyle{ d\in{D} }[/math] происходит с вероятностью [math]\displaystyle{ P(d) }[/math]. Условные вероятности [math]\displaystyle{ P(c|z) }[/math] и [math]\displaystyle{ P(z|d) }[/math] используются для описания зависимостей между наличием ссылки [math]\displaystyle{ c\in{C} }[/math] , латентным фактором [math]\displaystyle{ z\in{Z} }[/math] и документом [math]\displaystyle{ d\in{D} }[/math].
Оценивается функция правдоподобия:
- [math]\displaystyle{ L(C|D)=\prod^\ _{c\in{C},d\in{D}}P(d,c)=\prod^\ _{c\in{C},d\in{D}}P(d)P(c|d) }[/math],
- [math]\displaystyle{ P(c|d)=\sum_{z\in{Z}} P(c|z)P(z|d) }[/math]
Цель алгоритма PHITS состоит в том, чтобы подобрать [math]\displaystyle{ P(z) }[/math], [math]\displaystyle{ P(c|z) }[/math], [math]\displaystyle{ P(z|d) }[/math] для максимизации [math]\displaystyle{ L(C|D) }[/math] .
После этого:
[math]\displaystyle{ P(c|z) }[/math] – ранги "авторов";
[math]\displaystyle{ P(z|d) }[/math] – ранги "посредников".
Для вычисления рангов необходимо задать количество факторов в множестве [math]\displaystyle{ Z }[/math], и тогда [math]\displaystyle{ P(c|z) }[/math] будет характеризовать качество страницы как «автора» в контексте тематики. К недостаткам метода надо отнести то, что итеративный процесс чаще всего останавливается не на абсолютном, а на локальном максимуме функции правдоподобия [math]\displaystyle{ L }[/math]. Вместе с тем в ситуациях, когда в множестве найденных веб-страниц нет явного доминирования тематики запроса, PHITS превосходит алгоритм HITS.
- Автоматически генерируемые ссылки.
Некоторые из ссылок генерируются компьютером, но алгоритм HITS по-прежнему дает им равные значения.
- Нерелевантные документы.
Некоторые запросы могут возвращать на высокое место в рейтинге нерелевантные документы, что приводит к ошибочным результатам работы алгоритма HITS.
Примечания
- ↑ Перейти обратно: 1,0 1,1 Крижановский, 2008, с. 27.
- ↑ The metric of HITS, 2005, с. 55.
- ↑ Kleinberg, 1999.
- ↑ Перейти обратно: 4,0 4,1 4,2 Algorithm HITS, 2009.
- ↑ Hubs and authorities, 2010, с. 5.
- ↑ PageRank and HITS, 2010, с. 257.
- ↑ Problems with the HITS algorithm, 2011, с. 255.
Литература
- Ландэ Д.В.,Снарский А.А.,Безсуднов И.В. Интернетика. Навигация в сложных сетях: модели и алгоритмы. — Либроком, 2009. — 264 с. — ISBN 978-5-397-00497-8.
- Cronin B. Annual Review of Information Science and Technology (англ.). — 2004. — 674 p. — ISBN 1573872091.
- Kleinberg J. Authoritative sources in a hyperlinked environment (англ.). — 1999.
- Клейнберг Дж. Алгоритм HITS: авторитетные источники в гиперссылочной среде / перевод С. Неиленко. — 1999. Архивировано 12 октября 2013 года.
- Gupta G.K. Introduction to Data Mining with Case Studies: 2nd Edition (англ.). — PHI Learning Pvt. Ltd., 2011. — 491 p. — ISBN 978-81-203-4326-9.
- Leo J.G., Jonathan R.P. Discrete Calculus. Applied Analysis on Graphs for Computational Science (англ.). — Springer, 2010. — 366 p. — ISBN 978-1-84996-289-6. (недоступная ссылка)
- Scime A. Web Mining: Applications and Techniques (англ.). — Idea Group Inc., 2005. — 433 p. — ISBN 1591404150.
- Крижановский А.А. Кандидатская диссертация. Математическое и программное обеспечение построения списков семантически близких слов на основе рейтинга вики-текстов. — СПб., 2008. — С. 27—30. — 188 с.
- Chandranna A.K. An Online Versions of Hyperlinked-Induced Topics Search (HITS) Algorithm (англ.). — 2010.