Алгоритм Чена

Алгоритм Чена — алгоритм построения выпуклой оболочки конечного множества точек на плоскости. Является комбинацией двух более медленных алгоритмов (сканирование по Грэхему [math]\displaystyle{ O(n \log n) }[/math] и заворачивание по Джарвису [math]\displaystyle{ O(n h) }[/math]). Недостатком сканирования по Грэхему является необходимость сортировки всех точек по полярному углу, что занимает достаточно много времени [math]\displaystyle{ O(n \log n) }[/math]. Заворачивание по Джарвису требует перебора всех точек для каждой из [math]\displaystyle{ h }[/math] точек выпуклой оболочки, что в худшем случае занимает [math]\displaystyle{ O(n^2) }[/math]. Назван по имени Тимоти М. Чана.

Алгоритм Чана построения выпуклой оболочки. Трудоёмкость [math]\displaystyle{ O(n\log h) }[/math], где [math]\displaystyle{ h }[/math] — количество точек в выпуклой оболочке.

Описание алгоритма

Идея алгоритма Чена заключается в изначальном делении всех точек на группы по [math]\displaystyle{ m }[/math] штук в каждой. Соответственно, количество групп равно [math]\displaystyle{ r = \left \lceil n/m \right \rceil }[/math]. Для каждой из групп строится выпуклая оболочка сканированием по Грэхему за [math]\displaystyle{ O(m \log m) }[/math], то есть для всех групп понадобится [math]\displaystyle{ O(r m \log m) = O(n \log m) }[/math] времени.

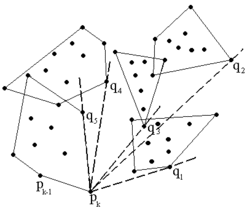
Затем, начиная с самой левой нижней точки, для получившихся в результате разбиения оболочек строится общая выпуклая оболочка по Джарвису. При этом следующая подходящая для выпуклой оболочки точка находится за [math]\displaystyle{ O(r \log m) }[/math], так как для того, чтобы найти точку с максимальным тангенсом по отношению к рассматриваемой точке в [math]\displaystyle{ m }[/math]-угольнике достаточно затратить [math]\displaystyle{ O(\log m) }[/math] (точки в [math]\displaystyle{ m }[/math]-угольнике были отсортированы по полярному углу во время выполнения алгоритма сканирования Грэхема). В итоге, на обход требуется [math]\displaystyle{ O(h r \log m) = O\left(\left(hn/m\right)\log m\right) }[/math] времени.

То есть алгоритм Чана работает за [math]\displaystyle{ O\left(\left(n + hn/m\right)\log m\right) }[/math], при этом, если получить [math]\displaystyle{ m = h }[/math], то за [math]\displaystyle{ O(n \log h) }[/math].

Hull(P, m)
 1)взять [math]\displaystyle{ r = \left \lceil n/m \right \rceil }[/math]. Разделить [math]\displaystyle{ P }[/math] на [math]\displaystyle{ r }[/math] дизъюнктных подмножеств [math]\displaystyle{ P_1,\;P_2,\;\ldots,\;P_r }[/math] мощности не более [math]\displaystyle{ m }[/math];
 2)for i = 1 to r do:
     (a) вычислить выпуклую оболочку Graham([math]\displaystyle{ P_i }[/math]), сохранить вершины в отсортированном по полярному углу массиве;
 3)в качестве [math]\displaystyle{ p_1 }[/math] взять самую левую и нижнюю точку из [math]\displaystyle{ P }[/math];
 4)for k = 1 to m do
     (a) for i = 1 to r do
             найти и запомнить точку [math]\displaystyle{ q_i }[/math] из [math]\displaystyle{ P_i }[/math] с максимальным углом [math]\displaystyle{ p_{k-1}p_{k}q_i }[/math];
     (b) взять в качестве [math]\displaystyle{ p_{k+1} }[/math] точку [math]\displaystyle{ q }[/math] из [math]\displaystyle{ {q_1,\;q_2,\;\ldots,\;q_r} }[/math] с максимальным углом [math]\displaystyle{ p_{k-1}p_{k}q }[/math];
     (c) if [math]\displaystyle{ p_{k+1} = p_1 }[/math] return [math]\displaystyle{ {p_1,\;\ldots,\;p_k} }[/math];
 5) return [math]\displaystyle{ m }[/math] маленькое, попробуйте еще;

Выбор числа точек m

Ясно, что обход по Джарвису, а следовательно и весь алгоритм, будет корректно работать только если [math]\displaystyle{ m \geqslant h }[/math], но как заранее узнать, сколько точек будет в выпуклой оболочке? Надо запускать алгоритм несколько раз, подбирая [math]\displaystyle{ m }[/math] и, если [math]\displaystyle{ m \lt h }[/math], то алгоритм будет возвращать ошибку. Если делать подбор бинарным поиском по [math]\displaystyle{ n }[/math], то в итоге получится время [math]\displaystyle{ O((n \log h)\log n) = O(n \log n) }[/math], что достаточно долго.

Процесс можно ускорить, если начать с маленького значения и после значительно его увеличивать, пока не получится [math]\displaystyle{ m \geqslant h }[/math]. Например, взять [math]\displaystyle{ 2^{2^t} }[/math]. При этом [math]\displaystyle{ t }[/math]-я итерация займет [math]\displaystyle{ O(n \log 2^{2^t}) = O(n 2^t) }[/math]. Процесс поиска завершится, когда [math]\displaystyle{ 2^{2^t} \geqslant h }[/math], то есть [math]\displaystyle{ t = \lceil \mathrm{lg}\, \mathrm{lg}\, h \rceil }[/math] ([math]\displaystyle{ \mathrm{lg} }[/math] — двоичный логарифм).

В итоге [math]\displaystyle{ \sum_{t=1}^{\mathrm{lg}\, \mathrm{lg}\, h} n 2^t = n \sum_{t=1}^{\mathrm{lg}\, \mathrm{lg}\, h} 2^t \leqslant n 2^{1 + \mathrm{lg}\, \mathrm{lg}\, h} = 2 n \,\mathrm{lg}\, h = O(n \log h) }[/math].

ChanHull(P)
 for t = 1 to n do:
     (a) взять [math]\displaystyle{ m = \min(2^{2^t},\; n) }[/math];
     (b) L = Hull(P, m);
     (c) if L != «[math]\displaystyle{ m }[/math] маленькое, попробуйте еще» return L;

Литература

• David M. Mount. Computational Geometry. — University of Maryland, 2002. — 122 с.