Квадрат (алгебра)
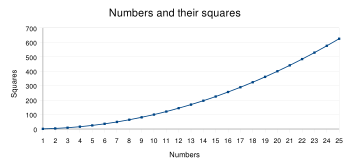
Квадра́т числа [math]\displaystyle{ x }[/math] — результат умножения числа на себя: [math]\displaystyle{ x \cdot x }[/math]. Обозначение: [math]\displaystyle{ x^2 }[/math].
Вычисление [math]\displaystyle{ x^2 }[/math] — математическая операция, называемая возведе́нием в квадра́т. Эта операция представляет собой частный случай возведения в степень, а именно — возведение числа [math]\displaystyle{ x }[/math] в степень 2.
Далее приведено начало числовой последовательности для квадратов целых неотрицательных чисел (последовательность A000290 в OEIS):
- 0, 1, 4, 9, 16, 25, 36, 49, 64, 81, 100, 121, 144, 169, 196, 225, 256, 289, 324, 361, 400, 441, 484, 529, 576, 625, 676, 729, 784, 841, 900, 961, 1024, 1089, 1156, 1225, 1296, 1369, 1444, 1521, 1600, 1681, 1764, 1849, 1936, 2025, 2116, 2209, 2304, 2401, 2500, …
Исторически натуральные числа из этой последовательности называли «квадратными».
Способы представления
Квадрат натурального числа [math]\displaystyle{ n }[/math] можно представить в виде суммы первых [math]\displaystyle{ n }[/math] нечетных чисел:
- 1: [math]\displaystyle{ 1 = 1 }[/math]
- 2: [math]\displaystyle{ 4 = 1 + 3 }[/math]
- …
- 7: [math]\displaystyle{ 49 = 1 + 3 + 5 + 7 + 9 + 11 + 13 }[/math]
- …
Ещё один способ представления квадрата натурального числа:
[math]\displaystyle{ n^2 = 1 + 1 + 2 + 2 + \ldots + (n - 1) + (n - 1) + n }[/math]
Пример:
- 1: [math]\displaystyle{ 1 = 1 }[/math]
- 2: [math]\displaystyle{ 4 = 1 + 1 + 2 }[/math]
- …
- 4: [math]\displaystyle{ 16 = 1 + 1 + 2 + 2 + 3 + 3 + 4 }[/math]
- …
Сумма квадратов первых [math]\displaystyle{ n }[/math] натуральных чисел вычисляется по формуле:
[math]\displaystyle{ \sum_{k=1}^n k^2 = 1^2 + 2^2 + 3^2 + \ldots + n^2 = \frac {n(n + 1)(2n + 1)} {6} }[/math]
Способ 1, метод приведения:
- Рассмотрим сумму кубов натуральных чисел от 1 до [math]\displaystyle{ n+1 }[/math]:
- [math]\displaystyle{ \sum_{k=1}^n k^3 + (n+1)^3 = \sum_{k=0}^n (k+1)^3 = \sum_{k=0}^n (k^3 + 3k^2 + 3k + 1) = \sum_{k=0}^n k^3 + \sum_{k=0}^n 3k^2 + \sum_{k=0}^n 3k + \sum_{k=0}^n 1 = \sum_{k=0}^n k^3 +3\sum_{k=0}^n k^2 +3\sum_{k=0}^n k + \sum_{k=0}^n 1 }[/math]
- Получим:
- [math]\displaystyle{ (n+1)^3 = 3\sum_{k=0}^n k^2 +3\sum_{k=0}^n k + \sum_{k=0}^n 1 = 3\sum_{k=0}^n k^2 + 3\frac{(n+1)n} {2} + (n + 1) }[/math]
- Умножим на 2 и перегруппируем:
- [math]\displaystyle{ 6\sum_{k=0}^n k^2 = 2(n + 1)^3 - 3(n + 1)n - 2(n + 1) = (n + 1)(2(n + 1)^2 - 3n - 2) = (n + 1)(2n^2 + n) = n(n + 1)(2n + 1) }[/math]
- [math]\displaystyle{ \sum_{k=0}^n k^2 = \frac {n(n + 1)(2n + 1)} {6} }[/math] (В рассуждениях использована формула: [math]\displaystyle{ \sum_{k=0}^n k = \frac{(n + 1)n} {2} }[/math], вывод которой аналогичен приведенному)
Способ 2, метод неизвестных коэффициентов:
- Заметим, что сумма функций степени [math]\displaystyle{ N }[/math] может быть выражена как функция [math]\displaystyle{ N+1 }[/math] степени. Исходя из этого факта предположим:
- [math]\displaystyle{ \sum_{k=0}^n k^2 = f(n) = An^3 + Bn^2 + Cn + D }[/math]
- [math]\displaystyle{ f(0) = 0 ; f(1) = 1 ; f(2) = 5 ; f(3) = 14 }[/math]
- Получим систему линейных уравнений относительно искомых коэффициентов:
- [math]\displaystyle{ \begin{cases} 0A + 0B + 0C + D = 0 \\ A + B + C + D= 1 \\ 8A + 4B + 2C + D = 5\\ 27A + 9B + 3C + D = 14 \\ \end{cases} }[/math]
- Решив её, получим [math]\displaystyle{ A = \frac{1} {3}, B = \frac{1} {2}, C = \frac{1} {6}, D = 0 }[/math]
- Таким образом:
- [math]\displaystyle{ \sum_{k=0}^n k^2 = f(n) = \frac{1} {3}n^3 + \frac{1} {2}n^2 + \frac{1} {6}n + 0 = \frac {n(n + 1)(2n + 1)} {6} }[/math]
Квадрат комплексного числа
Квадрат комплексного числа в алгебраической форме можно вычислить по формуле:
- [math]\displaystyle{ \left(a+bi\right)^2 = \left(a^2 - b^2\right) + 2abi. }[/math]
Аналогичная формула для комплексного числа в тригонометрической форме:
- [math]\displaystyle{ \left(r\left(\cos\phi+i\sin\phi\right)\right)^2 = r^2\left(\cos{2\phi}+i\sin{2\phi}\right). }[/math]
Геометрический смысл
Квадрат числа равен площади квадрата со стороной, равной этому числу.
Литература
- Грэхем Р., Кнут Д., Паташник О. — Конкретная математика. Основание информатики. Пер. с англ. —М.: Мир, 1998. —703 с.
См. также
- Извлечение квадратного корня — обратная операция по отношению к возведению в квадрат.
- Квадратное число
- Куб числа
- Обобщение на более высокие степени на Вольфраме Архивная копия от 2 июля 2012 на Wayback Machine.