Когерентность (физика)
Когерентность (от лат. cohaerens — «находящийся в связи») — в физике скоррелированность (согласованность) нескольких колебательных или волновых процессов во времени, проявляющаяся при их сложении. Колебания когерентны, если разность их фаз постоянна во времени, и при сложении колебаний получается колебание той же частоты.
Классический пример двух когерентных колебаний — это два синусоидальных колебания одинаковой частоты.
Когерентность волны означает, что в различных пространственных точках волны колебания происходят синхронно, то есть разность фаз между двумя точками не зависит от времени. Отсутствие когерентности, следовательно — ситуация, когда разность фаз между двумя точками не постоянна, а меняется со временем. Такая ситуация может иметь место, если волна была сгенерирована не единым излучателем, а совокупностью одинаковых, но независимых (то есть нескоррелированных) излучателей.
Изучение когерентности световых волн приводит к понятиям временно́й и пространственной когерентности. При распространении электромагнитных волн в волноводах могут иметь место фазовые сингулярности. В случае волн на воде когерентность волны определяет так называемая вторая периодичность.
Без когерентности невозможно наблюдать такое явление, как интерференция.
Радиус когерентности — расстояние, при смещении на которое вдоль псевдо-волновой поверхности, случайное изменение фазы достигает значения порядка π.
Процесс декогеренции — нарушение когерентности, вызываемое взаимодействием частиц с окружающей средой.
Временная когерентность
Понятие временно́й когерентности можно связать с контрастом интерференционной картины, наблюдаемой в результате интерференции двух волн, исходящих из одной и той же точки поперечного сечения пучка (полученных методом деления амплитуд). Временна́я когерентность волны характеризует сохранение взаимной когерентности при временном отставании одного из таких лучей по отношению к другому. При этом мерой временной когерентности служит время когерентности — максимально возможное время отставания одного луча по отношению к другому, при котором их взаимная когерентность ещё сохраняется. Временная когерентность определяется степенью монохроматичности.
Временной аспект когерентности имеет исключительно важное значение при рассмотрении явлений взаимодействия электромагнитных волн ввиду того, что в строгом смысле на практике монохроматических волн и волн с абсолютно одинаковыми частотами не существует из-за статистического характера излучения электромагнитных волн. Монохроматические волны представляют собой бесконечный по продолжительности и локализации пространственно-временной процесс, что очевидно невозможно с точки зрения предположений о конечности энергии источников электромагнитных волн, а ввиду конечного времени излучения, его спектр также имеет ненулевую ширину.
Если разность фаз двух колебаний изменяется очень медленно, то говорят, что колебания остаются когерентными в течение некоторого времени [math]\displaystyle{ \tau_{coh} }[/math]. Это время [math]\displaystyle{ \tau_{coh} }[/math] называют временем когерентности.
Можно сравнить фазы одного и того же колебания в разные моменты времени [math]\displaystyle{ t_{1} }[/math] и [math]\displaystyle{ t_{2} }[/math], разделённые интервалом [math]\displaystyle{ \tau_{coh} }[/math]. Если негармоничность колебания проявляется в беспорядочном, случайном изменении во времени его фазы, то при достаточно большом [math]\displaystyle{ \tau_{coh} }[/math] изменение фазы колебания может отклониться от гармонического закона. Это означает, что через время когерентности [math]\displaystyle{ \tau_{coh} }[/math] гармоническое колебание «забывает» свою первоначальную фазу и становится некогерентным «само себе».
Для описания подобных процессов (а также процессов излучения конечной длительности) вводят понятие цуг волн — «отрезок» монохроматической волны, конечной длины. Длительность цуга [math]\displaystyle{ \tau_{coh} }[/math] и будет временем когерентности, а длина [math]\displaystyle{ l_{coh}=c\tau_{coh} }[/math] — длиной когерентности ([math]\displaystyle{ c }[/math] — скорость распространения волны). По истечении одного гармонического цуга он как бы заменяется другим с той же частотой, но другой фазой.
На практике монохроматические волны представляются в виде цугов конечной длительности по времени, представляющих собой гармонические во времени функции, ограниченные во времени и пространстве.
Эксперимент с интерферометром Майкельсона
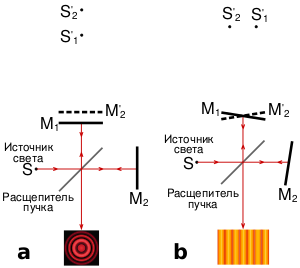
Проиллюстрируем понятие временной когеретности на примере эксперимента с интерферометром Майкельсона[1]. Предположим, что источник S испускает квазимонохроматический свет, то есть ширина полосы частот [math]\displaystyle{ \Delta \nu }[/math] мала по сравнению со средней частотой. Предположим, что путь при отражении от зеркала [math]\displaystyle{ M_2 }[/math] на расстояние 2d длиннее, чем при отражении от зеркала [math]\displaystyle{ M_1 }[/math]. Тогда разность хода [math]\displaystyle{ 2d=\Delta l=c \Delta t }[/math].
Интерференционные полосы будут возникать в том случае, когда выполнено условие
[math]\displaystyle{ \Delta t\Delta \nu \leq 1 }[/math].
Время [math]\displaystyle{ \Delta t }[/math] называется временем когерентности, а разность хода [math]\displaystyle{ \Delta l=c \Delta t \sim \frac{c}{\Delta \nu} }[/math] — продольной длиной когерентности.
Так как [math]\displaystyle{ \Delta \nu\sim \frac{c \Delta\lambda}{\overline\lambda^2} }[/math], где [math]\displaystyle{ \overline\lambda }[/math] — средняя длина волны, то можно написать
[math]\displaystyle{ \Delta l=\frac{\overline\lambda}{\Delta\lambda}\overline\lambda }[/math]. Каждая частотная компонента создает в пространстве свое распределение интенсивности, и распределения, созданные разными частотами, будут иметь разные условия максимумов и минимумов. В какой-то момент максимумы одних частот начинают накладываться на минимумы для других, и интерференционная картина смазывается.
Например, доплеровское уширение спектральной линии составляет порядка [math]\displaystyle{ 10^{-1}-10^{-2}\AA }[/math], тогда длина когеретности будет порядка нескольких миллиметров.
Получим условие [math]\displaystyle{ \Delta t\Delta \nu \leq 1 }[/math] на примере прямоугольного спектра. В интерферометре Майкельсона интенсивность на экране выражается формулой
[math]\displaystyle{ I =2I_0+2I_0 \cos(2kd \cos(\alpha))=2I_0+2I_0 \cos\left(\frac{2 \pi \nu}{ c} 2d \cos(\alpha)\right) }[/math]
здесь [math]\displaystyle{ \alpha=r/L }[/math], где r — радиус кольца (радиус точки на экране), а L — расстояние до зеркала, 2d- разность пути двух интерферирующих лучей.
Пусть частота принимает значения от [math]\displaystyle{ \nu-\Delta\nu/2 }[/math] до [math]\displaystyle{ \nu+\Delta\nu/2 }[/math] и спектр прямоугольный.
Сложим интенсивности от всех входящих частотных компонент
[math]\displaystyle{ I_{int} =2I_0+2I_0\frac{1}{\Delta\nu}\int_{\nu-\Delta\nu/2}^{\nu+\Delta\nu/2}\cos\left(\frac{2 \pi y}{ c} 2d \cos(\alpha)\right)dy=2I_0+2I_0\frac{1}{\Delta\nu}\frac{\sin\left(\frac{2 \pi (\nu+\Delta\nu/2)}{c} 2d \cos(\alpha)\right)-\sin\left(\frac{2 \pi (\nu-\Delta\nu/2)}{c} 2d \cos(\alpha)\right)}{\frac{2 \pi }{c} 2d \cos(\alpha)}= }[/math]

[math]\displaystyle{ =2I_0+2I_0\frac{\sin\left(\frac{\pi (\Delta\nu)}{c} 2d \cos(\alpha)\right)}{\frac{\pi\Delta\nu }{c} 2d \cos(\alpha)}\cos\left(2kd \cos(\alpha)\right) }[/math]
отсюда видно, что график интенсивности теперь содержит огибающую [math]\displaystyle{ \sin(x)/x }[/math], и видность колец значительно ослабевает при [math]\displaystyle{ x \approx 2 \pi }[/math].
тогда
[math]\displaystyle{ \frac{\pi\Delta\nu }{c} 2d \cos(\alpha) \approx 2 \pi }[/math]
поскольку [math]\displaystyle{ \cos(\alpha) \approx 1 }[/math], приходим к условию [math]\displaystyle{ \frac{2d}{c} \Delta\nu=\Delta t \Delta\nu \approx 1 }[/math] для наблюдения интерференции.
Пространственная когерентность
Пространственная когерентность — когерентность колебаний, которые совершаются в один и тот же момент времени в разных точках плоскости, перпендикулярной направлению распространения волны.
Понятие пространственной когерентности введено для[источник не указан 4609 дней] объяснения явления интерференции (на экране) от двух разных источников (от двух точек удлиненного источника, от двух точек круглого источника и т. п.).
Так, при определённом расстоянии от источников разность оптического хода будет такой, что фазы двух волн будут отличаться. В результате этого приходящие волны от различных частей источника в центр экрана будут уменьшать значение мощности по сравнению с максимальным, которое имело бы место, если бы все волны имели одинаковую фазу. На расстоянии, где разность оптического хода приведёт к тому, что фазы двух волн будут различаться ровно на π, сумма двух волн будет минимальна[2].
Пространственная когерентность на примере опыта Юнга

Рассмотрим эксперимент типа опыта Юнга, предполагая, что источник света протяженный (в одномерном случае длины [math]\displaystyle{ \Delta l }[/math]) и квазимонохроматический, при этом каждая точка источника излучает независимо от соседней (все точки некогерентны между собой). Возникновение полос от такого источника при интерференции на двух щелях будет проявлением пространственной когерентности[1]. Установлено, что полосы будут наблюдаться если выполнено условие
[math]\displaystyle{ \Delta l \Delta \theta \leq \lambda }[/math]
где [math]\displaystyle{ \Delta \theta \approx \frac{d}{H} }[/math] — угол под которым видны две щели из источника.
В случае двумерного квадратного источника со стороной [math]\displaystyle{ \Delta l }[/math] отверстия должны быть расположены на экране в пределах области с площадью
[math]\displaystyle{ \Delta A \approx (H \Delta \theta)^2 \approx \frac{H^2 \lambda^2}{\Delta l^2} }[/math]
Эта область называется площадью когерентности в плоскости экрана, а корень из неё иногда называют поперечной длиной когерентности или радиусом когерентности.
Можно показать[3], что условие действительно выполнено, сложив интенсивность интерференционных картин, получающихся при интерференции от каждой точки протяженного источника по отдельности.
При этом разность путей [math]\displaystyle{ \Delta s_{tot} }[/math] при прохождении света от точки источника до каждой из щелей вычисляется так же, как и в опыте Юнга [math]\displaystyle{ \Delta s_{tot}=\frac{xd}{L}+\frac{y \cdot d}{H} }[/math], где y — координата точки на источнике.
[math]\displaystyle{ I =2I_0+2I_0 \cos\left(k\frac{xd}{L}+k\frac{yd}{H}\right) }[/math]
[math]\displaystyle{
I_{int} =2I_0+2I_0\frac{1}{\Delta l}\int_{-\Delta l/2}^{\Delta l/2}\cos\left(k\frac{xd}{L}+k\frac{yd}{H}\right)dy =2I_0+2I_0\frac{\sin\left(k\frac{\Delta l \cdot d}{2H}\right)}{k\frac{\Delta l \cdot d}{2H}}\cos\left(k\frac{xd}{L}\right)
}[/math]
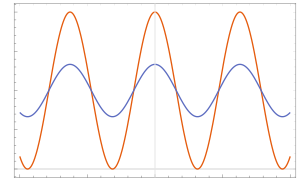
В этом случае интенсивность на экране имеет вид косинуса, но амплитуда его уменьшается по закону sinc в зависимости от протяженности источника.
Видность существенно падает, когда [math]\displaystyle{ k\frac{\Delta l \cdot d}{2H}=k\frac{\Delta l \Delta \theta}{2}\approx 2 \pi }[/math], что соответствует условию [math]\displaystyle{ \Delta l \Delta \theta \leq \lambda }[/math].
Радиус и площадь когерентности также можно выразить через угол, под которым видно источник из точки на экране. [math]\displaystyle{ \Delta A = \frac{H^2 \lambda^2}{\Delta l^2}= \frac{\lambda^2}{ \Omega} }[/math], где [math]\displaystyle{ \Omega }[/math] — телесный угол, под которым видно протяженный в двух направлениях источник, и, аналогично, [math]\displaystyle{ r_{coh}=\frac{\lambda}{\varphi} }[/math].
Примечания
- ↑ 1,0 1,1 Мандель Л., Вольф Э.Оптическая когерентность и квантовая оптика. М.: Физматлит, 2000.
- ↑ Г. Колфилд. Оптическая голография = Handbook of Optical Holography (англ.) / С. Б. Гуревич. — М.: «Мир», 1982. — Vol. 1. [1] Архивная копия от 24 июня 2016 на Wayback Machine
- ↑ И. В. Митин, Лабораторный практикум по физике. Оптика. Изучение влияния размеров источника света на видность интерференционной картины Физический факультет МГУ. [2] Архивная копия от 10 июля 2019 на Wayback Machine
В статье не хватает ссылок на источники (см. также рекомендации по поиску). |