Топологическая сортировка

Топологическая сортировка — упорядочивание вершин бесконтурного ориентированного графа согласно частичному порядку, заданному ребрами орграфа на множестве его вершин.

Пример

Для графа [math]\displaystyle{ G=\Bigl ( \bigl \{2, 3, 5, 7, 8, 9, 10, 11 \bigr \}, \bigl \{(3, 8), (3, 10), (5, 11), (7, 11), (7, 8), (8, 9), (11, 2), (11, 9), (11, 10)\bigr \}\Bigr ) }[/math]

Бесконтурный ориентированный граф

существует несколько согласованных последовательностей его вершин, которые могут быть получены при помощи топологической сортировки, например:

• [math]\displaystyle{ 7, 5, 11, 3, 8, 2, 9, 10 }[/math]
• [math]\displaystyle{ 3, 7, 5, 8, 11, 10, 9, 2 }[/math]

Видно, что в последовательности могут быть переставлены любые две стоящие рядом вершины, которые не входят в отношение частичного порядка [math]\displaystyle{ E }[/math].

Алгоритм Кана (1962)

Один из первых алгоритмов, и наиболее приспособленный к исполнению вручную.

Пусть дан бесконтурный ориентированный простой граф [math]\displaystyle{ G=(V, E) }[/math]. Через [math]\displaystyle{ A(v), v \in V }[/math] обозначим множество таких вершин [math]\displaystyle{ u \in V }[/math], что [math]\displaystyle{ \exists~ (u, v) \in E }[/math]. То есть [math]\displaystyle{ A(v) }[/math] — множество всех вершин, из которых есть дуга в вершину [math]\displaystyle{ v }[/math]. Пусть [math]\displaystyle{ P }[/math] — искомая последовательность вершин.

пока [math]\displaystyle{ |P| \lt  |V| }[/math]
  выбрать любую вершину [math]\displaystyle{ v }[/math] такую, что [math]\displaystyle{ A(v) = \varnothing }[/math] и [math]\displaystyle{ v \notin P }[/math]
  [math]\displaystyle{ P \gets P, v }[/math]
  удалить [math]\displaystyle{ v }[/math] из всех [math]\displaystyle{ A(u), u \neq v }[/math]

Наличие хотя бы одного контура в графе приведёт к тому, что на определённой итерации цикла не удастся выбрать новую вершину [math]\displaystyle{ v }[/math].

Пример работы алгоритма

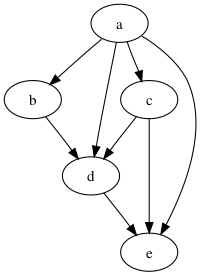
Пусть задан граф [math]\displaystyle{ G = \Bigl ( \bigl \{a, b, c, d, e \bigr \}, \bigl \{(a, b), (a, c), (a, d), (a, e), (b, d), (c, d), (c, e), (d,e) \bigr \} \Bigr ) }[/math]. В таком случае алгоритм выполнится следующим образом:

шаг	[math]\displaystyle{ v }[/math]	[math]\displaystyle{ A(a) }[/math]	[math]\displaystyle{ A(b) }[/math]	[math]\displaystyle{ A(c) }[/math]	[math]\displaystyle{ A(d) }[/math]	[math]\displaystyle{ A(e) }[/math]	[math]\displaystyle{ P }[/math]
0	[math]\displaystyle{ - }[/math]	[math]\displaystyle{ \varnothing }[/math]	[math]\displaystyle{ a }[/math]	[math]\displaystyle{ a }[/math]	[math]\displaystyle{ a, b, c }[/math]	[math]\displaystyle{ a, c, d }[/math]	[math]\displaystyle{ \varnothing }[/math]
1	[math]\displaystyle{ a }[/math]	[math]\displaystyle{ \varnothing }[/math]	[math]\displaystyle{ \varnothing }[/math]	[math]\displaystyle{ \varnothing }[/math]	[math]\displaystyle{ b, c }[/math]	[math]\displaystyle{ c, d }[/math]	[math]\displaystyle{ a }[/math]
2	[math]\displaystyle{ c }[/math]	[math]\displaystyle{ \varnothing }[/math]	[math]\displaystyle{ \varnothing }[/math]	[math]\displaystyle{ \varnothing }[/math]	[math]\displaystyle{ b }[/math]	[math]\displaystyle{ d }[/math]	[math]\displaystyle{ a, c }[/math]
3	[math]\displaystyle{ b }[/math]	[math]\displaystyle{ \varnothing }[/math]	[math]\displaystyle{ \varnothing }[/math]	[math]\displaystyle{ \varnothing }[/math]	[math]\displaystyle{ \varnothing }[/math]	[math]\displaystyle{ d }[/math]	[math]\displaystyle{ a, c, b }[/math]
4	[math]\displaystyle{ d }[/math]	[math]\displaystyle{ \varnothing }[/math]	[math]\displaystyle{ \varnothing }[/math]	[math]\displaystyle{ \varnothing }[/math]	[math]\displaystyle{ \varnothing }[/math]	[math]\displaystyle{ \varnothing }[/math]	[math]\displaystyle{ a, c, b, d }[/math]
5	[math]\displaystyle{ e }[/math]	[math]\displaystyle{ \varnothing }[/math]	[math]\displaystyle{ \varnothing }[/math]	[math]\displaystyle{ \varnothing }[/math]	[math]\displaystyle{ \varnothing }[/math]	[math]\displaystyle{ \varnothing }[/math]	[math]\displaystyle{ a, c, b, d, e }[/math]

На втором шаге вместо [math]\displaystyle{ c }[/math] может быть выбрана вершина [math]\displaystyle{ b }[/math], поскольку порядок между [math]\displaystyle{ b }[/math] и [math]\displaystyle{ c }[/math] не задан.

Алгоритм Тарьяна (1976)

На компьютере топологическую сортировку можно выполнить за O(n) времени и памяти, если обойти все вершины, используя поиск в глубину, и выводить вершины в момент выхода из неё.

Другими словами алгоритм состоит в следующем:

• Изначально все вершины белые.
• Для каждой вершины делаем шаг алгоритма.

Шаг алгоритма:

• Если вершина чёрная, ничего делать не надо.
• Если вершина серая — найден цикл, топологическая сортировка невозможна.
• Если вершина белая
  • Красим её в серый
  • Применяем шаг алгоритма для всех вершин, в которые можно попасть из текущей
  • Красим вершину в чёрный и помещаем её в начало окончательного списка.

Пример

Пример будет на том же графе, однако порядок, в котором выбираем вершины для обхода — c, d, e, a, b.

Шаг	Текущая	Белые	Стек (серые)	Выход (чёрные)
0	—	a, b, c, d, e	—	—
1	c	a, b, d, e	c	—
2	d	a, b, e	c, d	—
3	e	a, b	c, d, e	—
4	d	a, b	c, d	e
5	c	a, b	c	d, e
6	—	a, b	—	c, d, e
7	d	a, b	—	c, d, e
8	e	a, b	—	c, d, e
9	a	b	a	c, d, e
10	b	—	a, b	c, d, e
11	a	—	a	b, c, d, e
12	—	—	—	a, b, c, d, e
13	b	—	—	a, b, c, d, e

Применение

При помощи топологической сортировки строится корректная последовательность выполнения действий, всякое из которых может зависеть от другого: последовательность прохождения учебных курсов студентами, установки программ при помощи пакетного менеджера, сборки исходных текстов программ при помощи Makefile'ов.

Можно построить список отображения объектов в изометрической проекции зная парные порядковые отношения между объектами (какой из двух объектов должен быть прорисован раньше).

См. также

• Алгоритм Демукрона

Ссылки

• Пример алгоритма топологической сортировки на Python, C++, Pascal
• Топологическая сортировка при помощи поиска в глубину — реализация на C++
• Топологическая сортировка на Pascal за O(n + m) от Никлауса Вирта

Литература

• Шаблон:Source
• Кормен, Т., Лейзерсон, Ч., Ривест, Р., Штайн, К. Глава 22.4. Топологическая сортировка // Алгоритмы: построение и анализ = Introduction to Algorithms / Под ред. И. В. Красикова. — 2-е изд. — М.: Вильямс, 2005. — С. 632-635. — ISBN 5-8459-0857-4.