Теорема Пифагора

Эта статья находится на начальном уровне проработки, в одной из её версий выборочно используется текст из источника, распространяемого под свободной лицензией
Материал из энциклопедии Руниверсалис
Схема, объясняющая доказательство теоремы Пифагора через равнодополняемость[⇨]
Почтовая марка Никарагуа 1971 года и её оборот. Теорема Пифагора (длина сторон прямоугольного треугольника)

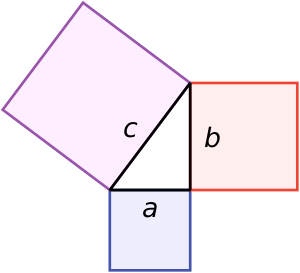
Теоре́ма Пифаго́ра — одна из основополагающих теорем евклидовой геометрии, устанавливающая соотношение между сторонами прямоугольного треугольника: сумма квадратов длин катетов равна квадрату длины гипотенузы.

Соотношение в том или ином виде предположительно было известно различным древним цивилизациям задолго до нашей эры; первое геометрическое доказательство приписывается Пифагору. Утверждение появляется как Предложение 47 в «Началах» Евклида[⇨].

Также может быть выражена как геометрический факт о том, что площадь квадрата, построенного на гипотенузе, равна сумме площадей квадратов, построенных на катетах. Верно и обратное утверждение[⇨]: треугольник, у которого сумма квадратов длин двух сторон равна квадрату длины третьей стороны, является прямоугольным.

Существует ряд обобщений данной теоремы[⇨] — для произвольных треугольников, для фигур в пространствах высших размерностей. В неевклидовых геометриях теорема не выполняется[⇨].

История

По мнению историка математики Морица Кантора, в Древнем Египте во времена царя Аменемхета I (около XXIII век до н. э.) было известно о прямоугольном треугольнике со сторонами 3, 4, 5 — его использовали гарпедонапты — «натягиватели верёвок»[1]. В древневавилонском тексте, относимом ко временам Хаммурапи (XX век до н. э.), приведено приближённое вычисление гипотенузы[2]. По мнению Ван-дер-Вардена, очень вероятно, что соотношение в общем виде было известно в Вавилоне уже около XVIII века до н. э.

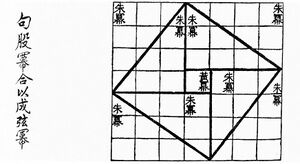
Рисунок из книги Чжоу би суань цзин (500—200 лет до нашей эры)

В древнекитайской книге «Чжоу би суань цзин», относимой к периоду V—III веков до н. э., приводится треугольник со сторонами 3, 4 и 5, притом изображение можно трактовать как графическое обоснование соотношения теоремы[3]. В китайском сборнике задач «Математика в девяти книгах» (X—II веков до н. э.) применению теоремы посвящена отдельная книга.

Общепринято, что доказательство соотношения дано древнегреческим философом Пифагором (570—490 до н. э.). Имеется свидетельство Прокла (412—485 н. э.), что Пифагор использовал алгебраические методы, чтобы находить пифагоровы тройки[⇨][4], но при этом в течение пяти веков после смерти Пифагора прямых упоминаний о доказательстве его авторства не находится. Однако когда Плутарх и Цицерон пишут о теореме Пифагора, из содержания следует, будто авторство Пифагора общеизвестно и несомненно[5][6]. Существует предание, сообщённое Диогеном Лаэртским, согласно которому Пифагор якобы отпраздновал открытие своей теоремы гигантским пиром, заклав на радостях сотню быков[7].

Приблизительно в 400 году до н. э., согласно Проклу, Платон дал метод нахождения пифагоровых троек, сочетающий алгебру и геометрию. Около 300 года до н. э. в «Началах» Евклида появилось старейшее аксиоматическое доказательство теоремы Пифагора[8].

Формулировки

Сумма площадей квадратов, опирающихся на катеты [math]\displaystyle{ a }[/math] и [math]\displaystyle{ b }[/math], равна площади квадрата, построенного на гипотенузе [math]\displaystyle{ c }[/math]

Основная формулировка содержит алгебраические действия — в прямоугольном треугольнике, длины катетов которого равны [math]\displaystyle{ a }[/math] и [math]\displaystyle{ b }[/math], а длина гипотенузы — [math]\displaystyle{ c }[/math], выполнено соотношение

[math]\displaystyle{ a^2 + b^2 = c^2. }[/math]

Возможна и эквивалентная геометрическая формулировка, прибегающая к понятию площади фигуры: в прямоугольном треугольнике площадь квадрата, построенного на гипотенузе, равна сумме площадей квадратов, построенных на катетах. В таком виде теорема сформулирована в «Началах» Евклида.

Обратная теорема Пифагора — утверждение о прямоугольности всякого треугольника, длины сторон которого связаны соотношением [math]\displaystyle{ a^2 + b^2 = c^2 }[/math]. Как следствие, для всякой тройки положительных чисел [math]\displaystyle{ a }[/math], [math]\displaystyle{ b }[/math] и [math]\displaystyle{ c }[/math], такой, что [math]\displaystyle{ a^2 + b^2 = c^2 }[/math], существует прямоугольный треугольник с катетами [math]\displaystyle{ a }[/math] и [math]\displaystyle{ b }[/math] и гипотенузой [math]\displaystyle{ c }[/math].

Доказательства

В научной литературе зафиксировано не менее 400 доказательств теоремы Пифагора[9], что объясняется как фундаментальным значением для геометрии, так и элементарностью результата. Основные направления доказательств: алгебраическое использование соотношений элементов треугольника (таков, например, популярный метод подобия[⇨]), метод площадей[⇨], существуют также различные экзотические доказательства (например, с помощью дифференциальных уравнений).

Через подобные треугольники

Podobnye treugolniki proof.png

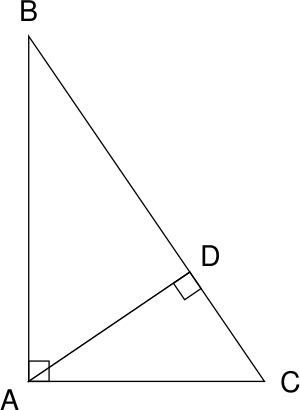
Одним из наиболее популярных в учебной литературе доказательств алгебраической формулировки является доказательство с использованием техники подобия треугольников, при этом оно почти непосредственно выводится из аксиом и не задействует понятие площади фигуры[10]. В нём для треугольника [math]\displaystyle{ \triangle ABC }[/math] с прямым углом при вершине [math]\displaystyle{ C }[/math] со сторонами [math]\displaystyle{ a, b, c }[/math], противолежащими вершинам [math]\displaystyle{ A, B, C }[/math] соответственно, проводится высота [math]\displaystyle{ CH }[/math], при этом (согласно признаку подобия по равенству двух углов) возникают соотношения подобия: [math]\displaystyle{ \triangle ABC \sim \triangle ACH }[/math] и [math]\displaystyle{ \triangle ABC \sim \triangle CBH }[/math], из чего непосредственно следуют соотношения

[math]\displaystyle{ \frac{a}{c} = \frac{|HB|}{a}, \quad \frac{b}{c} = \frac{|AH|}{b}. }[/math]

При перемножении крайних членов пропорций выводятся равенства

[math]\displaystyle{ a^2 = c \cdot |HB|, \quad b^2 = c \cdot |AH|, }[/math]

покомпонентное сложение которых даёт требуемый результат:

[math]\displaystyle{ a^2 + b^2 = c \cdot \big(|HB|+|AH|\big) = c^2 \quad \Leftrightarrow \quad a^2 + b^2 = c^2. }[/math]

Доказательства методом площадей

Большое число доказательств задействуют понятие площади. Несмотря на видимую простоту многих из них, такие доказательства используют свойства площадей фигур, доказательства которых сложнее доказательства самой теоремы Пифагора.

Доказательство через равнодополняемость

Схема доказательства через равнодополняемость

Доказательство через равнодополняемость использует четыре копии прямоугольного треугольника с катетами [math]\displaystyle{ a, b }[/math] и гипотенузой [math]\displaystyle{ c }[/math], расположенные таким образом, чтобы образовывать квадрат со стороной [math]\displaystyle{ a+b }[/math] и внутренний четырёхугольник со сторонами длиной [math]\displaystyle{ c }[/math]. Внутренний четырёхугольник в этой конфигурации является квадратом, так как сумма двух противоположных прямому острых углов — 90°, а развёрнутый угол — 180°. Площадь внешнего квадрата равна [math]\displaystyle{ (a+b)^2 }[/math], он состоит из внутреннего квадрата площадью [math]\displaystyle{ c^2 }[/math] и четырёх прямоугольных треугольников, каждый площадью [math]\displaystyle{ \frac{ab}{2} }[/math], в результате из соотношения [math]\displaystyle{ (a+b)^2=4\cdot\frac{ab}{2}+c^2 }[/math] при алгебраическом преобразовании следует утверждение теоремы.

Доказательство Евклида

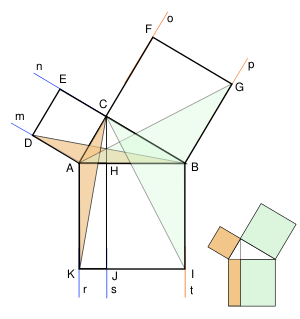
Чертёж к доказательству Евклида. Основное направление доказательства — установление конгруэнтности [math]\displaystyle{ \triangle ACK \cong \triangle ABD }[/math], площадь которых составляет половину площади прямоугольников [math]\displaystyle{ AHJK }[/math] и [math]\displaystyle{ ACED }[/math] соответственно

Классическое доказательство Евклида направлено на установление равенства площадей между прямоугольниками, образованными из рассечения квадрата над гипотенузой высотой из прямого угла с квадратами над катетами[11].

Конструкция, используемая для доказательства следующая: для прямоугольного треугольника [math]\displaystyle{ \triangle ABC }[/math] с прямым углом [math]\displaystyle{ C }[/math], квадратов над катетами [math]\displaystyle{ ACED }[/math] и [math]\displaystyle{ BCFG }[/math] и квадрата над гипотенузой [math]\displaystyle{ ABIK }[/math] строится высота [math]\displaystyle{ CH }[/math] и продолжающий её луч [math]\displaystyle{ s }[/math], разбивающий квадрат над гипотенузой на два прямоугольника [math]\displaystyle{ AHJK }[/math] и [math]\displaystyle{ BHJI }[/math]. Доказательство нацелено на установление равенства площадей прямоугольника [math]\displaystyle{ AHJK }[/math] с квадратом над катетом [math]\displaystyle{ AC }[/math]; равенство площадей второго прямоугольника, составляющего квадрат над гипотенузой, и прямоугольника над другим катетом устанавливается аналогичным образом.

Равенство площадей прямоугольника [math]\displaystyle{ AHJK }[/math] и [math]\displaystyle{ ACED }[/math] устанавливается через конгруэнтность треугольников [math]\displaystyle{ \triangle ACK }[/math] и [math]\displaystyle{ \triangle ABD }[/math], площадь каждого из которых равна половине площади прямоугольников [math]\displaystyle{ AHJK }[/math] и [math]\displaystyle{ ACED }[/math] соответственно в связи со следующим свойством: площадь треугольника равна половине площади прямоугольника, если у фигур есть общая сторона, а высота треугольника к общей стороне является другой стороной прямоугольника. Конгруэнтность треугольников следует из равенства двух сторон (стороны квадратов) и углу между ними (составленного из прямого угла и угла при [math]\displaystyle{ A }[/math]).

Таким образом, доказательством устанавливается, что площадь квадрата над гипотенузой, составленного из прямоугольников [math]\displaystyle{ AHJK }[/math] и [math]\displaystyle{ BHJI }[/math], равна сумме площадей квадратов над катетами.

Доказательство Леонардо да Винчи

Чертёж к доказательству, приписываемому Леонардо да Винчи

К методу площадей относится также доказательство, приписываемое Леонардо да Винчи. По данным немецкого математика Франца Леммермейера (нем. Franz Lemmermeyer), в действительности это доказательство было придумано Иоганном Тобиасом Майером[12]. Пусть дан прямоугольный треугольник [math]\displaystyle{ \triangle ABC }[/math] с прямым углом [math]\displaystyle{ C }[/math] и квадраты [math]\displaystyle{ ACED }[/math], [math]\displaystyle{ BCFG }[/math] и [math]\displaystyle{ ABHJ }[/math] (см. рисунок). В этом доказательстве на стороне [math]\displaystyle{ HJ }[/math] последнего во внешнюю сторону строится треугольник, конгруэнтный [math]\displaystyle{ \triangle ABC }[/math], притом отражённый как относительно гипотенузы, так и относительно высоты к ней (то есть [math]\displaystyle{ JI = BC }[/math] и [math]\displaystyle{ HI = AC }[/math]). Прямая [math]\displaystyle{ CI }[/math] разбивает квадрат, построенный на гипотенузе на две равные части, поскольку треугольники [math]\displaystyle{ \triangle ABC }[/math] и [math]\displaystyle{ \triangle JHI }[/math] равны по построению. Доказательство устанавливает конгруэнтность четырёхугольников [math]\displaystyle{ CAJI }[/math] и [math]\displaystyle{ DABG }[/math], площадь каждого из которых, оказывается, с одной стороны, равной сумме половин площадей квадратов на катетах и площади исходного треугольника, с другой стороны — половине площади квадрата на гипотенузе плюс площадь исходного треугольника. Итого, половина суммы площадей квадратов над катетами равна половине площади квадрата над гипотенузой, что равносильно геометрической формулировке теоремы Пифагора.

Через площади подобных треугольников

Следующее доказательство основано на том, что площади подобных треугольников относятся как квадраты соответственных сторон[13].

Altitude of a right triangle.svg

Пусть [math]\displaystyle{ ABC }[/math] есть прямоугольный треугольник, [math]\displaystyle{ AD }[/math] — перпендикуляр, опущенный на гипотенузу из вершины прямого угла. Треугольники [math]\displaystyle{ ABC }[/math], [math]\displaystyle{ DBA }[/math] подобны, так как имеют по прямому углу и ещё общий угол [math]\displaystyle{ B }[/math]. Значит

[math]\displaystyle{ \frac{\text{площадь}~DBA}{\text{площадь}~ABC}= \frac{AB^2}{BC^2}. }[/math]

Точно также получаем, что

[math]\displaystyle{ \frac{\text{площадь}~DAC}{\text{площадь}~ABC}= \frac{AC^2}{BC^2}. }[/math]

Поскольку треугольники [math]\displaystyle{ DBA }[/math] и [math]\displaystyle{ DAC }[/math] вместе составляют [math]\displaystyle{ \triangle ABC }[/math], сумма площадей [math]\displaystyle{ \triangle DBA }[/math] и [math]\displaystyle{ \triangle DAC }[/math] равна площади [math]\displaystyle{ \triangle ABC }[/math]. Отсюда

[math]\displaystyle{ \frac{AB^2+AC^2}{BC^2}=1 }[/math]

или [math]\displaystyle{ AB^2+AC^2=BC^2. }[/math]

Доказательство методом бесконечно малых

Доказательство методом бесконечно малых

Существует несколько доказательств, прибегающих к технике дифференциальных уравнений. В частности, Харди приписывается доказательство, использующее бесконечно малые приращения катетов [math]\displaystyle{ a }[/math] и [math]\displaystyle{ b }[/math] и гипотенузы [math]\displaystyle{ c }[/math]. Например, приращение катета [math]\displaystyle{ da }[/math] при постоянном катете [math]\displaystyle{ b }[/math] приводит к приращению гипотенузы [math]\displaystyle{ dc }[/math], так что

[math]\displaystyle{ \frac{da}{dc} = \frac{c}{a}. }[/math]

Методом разделения переменных из них выводится дифференциальное уравнение [math]\displaystyle{ c \,dc = a \,da }[/math], интегрирование которого даёт соотношение [math]\displaystyle{ c^2 = a^2 + \mathrm{const} }[/math]. Применение начальных условий [math]\displaystyle{ a = 0,\ c = b }[/math] определяет константу как [math]\displaystyle{ b^2 }[/math], что в результате даёт утверждение теоремы.

Квадратичная зависимость в окончательной формуле появляется благодаря линейной пропорциональности между сторонами треугольника и приращениями, тогда как сумма связана с независимыми вкладами от приращения разных катетов.

Вариации и обобщения

Подобные геометрические фигуры на трёх сторонах

Обобщение для подобных треугольников, сумма площадей зелёных фигур равна площади синей
Теорема Пифагора с использованием подобных прямоугольных треугольников

Важное геометрическое обобщение теоремы Пифагора дал Евклид в «Началах», перейдя от площадей квадратов на сторонах к площадям произвольных подобных геометрических фигур[14]: сумма площадей таких фигур, построенных на катетах, будет равна площади подобной им фигуры, построенной на гипотенузе.

Главная идея этого обобщения заключается в том, что площадь подобной геометрической фигуры пропорциональна квадрату любого своего линейного размера и в частности квадрату длины любой стороны. Следовательно, для подобных фигур с площадями [math]\displaystyle{ A }[/math], [math]\displaystyle{ B }[/math] и [math]\displaystyle{ C }[/math], построенных на катетах с длинами [math]\displaystyle{ a }[/math] и [math]\displaystyle{ b }[/math] и гипотенузе [math]\displaystyle{ c }[/math] соответственно, имеет место соотношение:

[math]\displaystyle{ \frac{A}{a^2} = \frac{B}{b^2} = \frac{C}{c^2}\, \Rightarrow \, A + B = \frac{a^2}{c^2}C + \frac{b^2}{c^2}C }[/math].

Так как по теореме Пифагора [math]\displaystyle{ a^2 + b^2 = c^2 }[/math], то выполнено [math]\displaystyle{ A + B = C }[/math].

Кроме того, если возможно доказать без привлечения теоремы Пифагора, что для площадей трёх подобных геометрических фигур на сторонах прямоугольного треугольника выполнено соотношение [math]\displaystyle{ A + B = C }[/math], то с использованием обратного хода доказательства обобщения Евклида можно вывести доказательство теоремы Пифагора. Например, если на гипотенузе построить конгруэнтный начальному прямоугольный треугольник площадью [math]\displaystyle{ C }[/math], а на катетах — два подобных ему прямоугольных треугольника с площадями [math]\displaystyle{ A }[/math] и [math]\displaystyle{ B }[/math], то оказывается, что треугольники на катетах образуются в результате деления начального треугольника его высотой, то есть сумма двух меньших площадей треугольников равна площади третьего, таким образом [math]\displaystyle{ A + B = C }[/math] и, применяя соотношение для подобных фигур, выводится теорема Пифагора.

Теорема косинусов

Основная статья: Теорема косинусов

Теорема Пифагора — это частный случай более общей теоремы косинусов, которая связывает длины сторон в произвольном треугольнике[15]:

[math]\displaystyle{ a^2+b^2-2ab\cos{\theta}=c^2 }[/math],

где [math]\displaystyle{ \theta }[/math] — угол между сторонами [math]\displaystyle{ a }[/math] и [math]\displaystyle{ b }[/math]. Если угол равен 90°, то [math]\displaystyle{ \cos \theta = 0 }[/math], и формула упрощается до обычной теоремы Пифагора.

Произвольный треугольник

Обобщение, установленное Сабитом ибн Куррой. Нижний рисунок демонстрирует подобие треугольника [math]\displaystyle{ \triangle DBA }[/math] треугольнику [math]\displaystyle{ \triangle ABC }[/math]

Существует обобщение теоремы Пифагора на произвольный треугольник, оперирующее исключительно соотношением длин сторон. Считается, что оно впервые было установлено сабийским астрономом Сабитом ибн Куррой[16]. В нём для произвольного треугольника со сторонами [math]\displaystyle{ a, b, c }[/math] в него вписывается равнобедренный треугольник с основанием на стороне [math]\displaystyle{ c }[/math], вершиной, совпадающей с вершиной исходного треугольника, противолежащей стороне [math]\displaystyle{ c }[/math] и углами при основании, равными углу [math]\displaystyle{ \theta }[/math], противолежащему стороне [math]\displaystyle{ c }[/math]. В результате образуются два треугольника, подобных исходному: первый — со сторонами [math]\displaystyle{ a }[/math], дальней от неё боковой стороной вписанного равнобедренного треугольника, и [math]\displaystyle{ r }[/math] — части стороны [math]\displaystyle{ c }[/math]; второй — симметрично к нему от стороны [math]\displaystyle{ b }[/math] со стороной [math]\displaystyle{ s }[/math] — соответствующей частью стороны [math]\displaystyle{ c }[/math]. В результате оказывается выполнено соотношение[17][18]

[math]\displaystyle{ a^2 + b^2 = c(r + s), }[/math]

вырождающееся в теорему Пифагора при [math]\displaystyle{ \theta = \pi/2 }[/math]. Соотношение является следствием подобия образованных треугольников:

[math]\displaystyle{ \frac{c}{a} = \frac{a}{r}, \quad \frac{c}{b} = \frac{b}{s} \quad \Rightarrow \quad cr + cs = a^2 + b^2. }[/math]

Теорема Паппа о площадях

Теорема Паппа о площадях, позволяющая для произвольного треугольника и произвольных параллелограммов на двух его сторонах построить параллелограмм на третьей стороне таким образом, чтобы его площадь была равна сумме площадей двух заданных параллелограммов, также может быть рассмотрена как обобщение теоремы Пифагора[19]: в случае, когда исходный треугольник — прямоугольный, а на катетах в качестве параллелограммов заданы квадраты, квадрат, построенный на гипотенузе оказывается удовлетворяющим условиям теоремы Паппа о площадях.

Многомерные обобщения

Обобщением теоремы Пифагора для трёхмерного евклидова пространства является теорема де Гуа: если в одной вершине тетраэдра сходятся три прямых угла, то квадрат площади грани, лежащей напротив этой вершины, равен сумме квадратов площадей других трёх граней. Этот вывод может быть обобщён и как «n-мерная теорема Пифагора» для евклидовых пространств высших размерностей[20] — для граней ортогонального [math]\displaystyle{ n }[/math]-мерного симплекса с площадями [math]\displaystyle{ S_1, \dots, S_n }[/math] ортогональных граней и противолежащей им грани площадью [math]\displaystyle{ S_0 }[/math] выполнено соотношение:

[math]\displaystyle{ S_0^2 = \sum_{i=1}^n S_i^2 }[/math].

Ещё одно многомерное обобщение возникает из задачи нахождения квадрата длины диагонали прямоугольного параллелепипеда: для её вычисления необходимо дважды применить теорему Пифагора, в результате она составит сумму квадратов длин трёх смежных сторон параллелепипеда. В общем случае, длина диагонали [math]\displaystyle{ n }[/math]-мерного прямоугольного параллелепипеда со смежными сторонами с длинами [math]\displaystyle{ a_1, \dots, a_n }[/math] составляет:

[math]\displaystyle{ d^2 = \sum_{i=1}^n a_i^2 }[/math],

как и в трёхмерном случае, результат является следствием последовательного применения теоремы Пифагора к прямоугольным треугольникам в перпендикулярных плоскостях.

Обобщением теоремы Пифагора для бесконечномерного пространства является равенство Парсеваля[21].

Неевклидова геометрия

Теорема Пифагора выводится из аксиом евклидовой геометрии и недействительна для неевклидовой геометрии[22] — выполнение теоремы Пифагора равносильно постулату Евклида о параллельности[23][24].

В неевклидовой геометрии соотношение между сторонами прямоугольного треугольника обязательно будет в форме, отличной от теоремы Пифагора. Например, в сферической геометрии все три стороны прямоугольного треугольника, которые ограничивают собой октант единичной сферы, имеют длину [math]\displaystyle{ \pi/2 }[/math], что противоречит теореме Пифагора.

При этом теорема Пифагора справедлива в гиперболической и эллиптической геометрии, если требование о прямоугольности треугольника заменить условием, что сумма двух углов треугольника должна равняться третьему[25].

Сферическая геометрия

Основная статья: Сферическая теорема Пифагора
Сферический треугольник

Для любого прямоугольного треугольника на сфере радиусом [math]\displaystyle{ R }[/math] (например, если угол [math]\displaystyle{ \gamma }[/math] в треугольнике прямой) со сторонами [math]\displaystyle{ a, b, c }[/math] соотношение между сторонами имеет вид[26]

[math]\displaystyle{ \cos\frac{c}{R} = \cos\frac{a}{R} \cdot \cos\frac{b}{R}. }[/math]

Это равенство может быть выведено как особый случай сферической теоремы косинусов, которая справедлива для всех сферических треугольников:

[math]\displaystyle{ \cos\frac{c}{R} = \cos\frac{a}{R} \cdot \cos\frac{b}{R} + \sin\frac{a}{R} \cdot \sin\frac{b}{R} \cdot \cos\gamma. }[/math]

Применяя ряд Тейлора в функции косинуса ([math]\displaystyle{ \cos x \approx 1 - \dfrac{x^2}{2} }[/math]) можно показать, что если радиус [math]\displaystyle{ R }[/math] стремится к бесконечности, а аргументы [math]\displaystyle{ \dfrac{a}{R} }[/math], [math]\displaystyle{ \dfrac{b}{R} }[/math] и [math]\displaystyle{ \dfrac{c}{R} }[/math] стремятся к нулю, то сферическое соотношение между сторонами в прямоугольном треугольнике приближается к теореме Пифагора.

Геометрия Лобачевского

Гиперболический треугольник

В геометрии Лобачевского для прямоугольного треугольника со сторонами [math]\displaystyle{ a, b, c }[/math] со стороной [math]\displaystyle{ c }[/math], противолежащей прямому углу, соотношение между сторонами будет следующим[27]:

[math]\displaystyle{ \operatorname{ch} c=\operatorname{ch} a \cdot \operatorname{ch} b }[/math],

где [math]\displaystyle{ \operatorname{ch} }[/math] — гиперболический косинус[28]. Эта формула является частным случаем гиперболической теоремы косинусов, которая справедлива для всех треугольников[29]:

[math]\displaystyle{ \operatorname{ch}c= \operatorname{ch} a \cdot \operatorname{ch} b - \operatorname{sh} a \cdot \operatorname{sh} b \cdot \cos \gamma }[/math],

где [math]\displaystyle{ \gamma }[/math] — угол, вершина которого противоположна стороне [math]\displaystyle{ c }[/math].

Используя ряд Тейлора для гиперболического косинуса ([math]\displaystyle{ \operatorname{ch}x \approx 1 + \dfrac{x^2}{2} }[/math]) можно показать, что если гиперболический треугольник уменьшается (то есть, когда [math]\displaystyle{ a }[/math], [math]\displaystyle{ b }[/math] и [math]\displaystyle{ c }[/math] стремятся к нулю), то гиперболические соотношения в прямоугольном треугольнике приближаются к соотношению классической теоремы Пифагора.

Применение

Расстояние в двумерных прямоугольных системах

Важнейшее применение теоремы Пифагора — определение расстояния между двумя точками в прямоугольной системе координат: расстояние [math]\displaystyle{ s }[/math] между точками с координатами [math]\displaystyle{ (a, b) }[/math] и [math]\displaystyle{ (c, d) }[/math] равно

[math]\displaystyle{ s = \sqrt{(a - c)^2 + (b - d)^2}. }[/math]

Для комплексных чисел теорема Пифагора даёт естественную формулу для нахождения модуля комплексного числа — для [math]\displaystyle{ z = x + yi }[/math] он равен длине радиус-вектора на комплексной плоскости к точке [math]\displaystyle{ (x, y) }[/math]:

[math]\displaystyle{ |z| = \sqrt{x^2 + y^2}. }[/math]

Расстояние между комплексными числами [math]\displaystyle{ z_1 = x_1 + y_1 i }[/math] и [math]\displaystyle{ z_2 = x_2 + y_2 i }[/math] также представляется в форме теоремы Пифагора[30]:

[math]\displaystyle{ |z_1 - z_2| = \sqrt{(x_1 - x_2)^2 + (y_1 - y_2)^2}. }[/math]

Расстояние между двумя точками в плоскости Лобачевского

[math]\displaystyle{ ds^2 = dx^2 + \operatorname{ch}^2\left(\frac{y}{R}\right) dy^2 }[/math].

Здесь R — радиус кривизны плоскости Лобачевского, ch — гиперболический косинус.

Евклидова метрика

Евклидова метрика — функция расстояния в евклидовых пространствах, определяемая по теореме Пифагора, непосредственным её применением в двумерном случае, и последовательным в многомерном; для точек [math]\displaystyle{ n }[/math]-мерного пространства [math]\displaystyle{ p = (p_1, \dots, p_n) }[/math] и [math]\displaystyle{ q = (q_1, \dots, q_n) }[/math] расстояние [math]\displaystyle{ d(p, q) }[/math] между ними определяется следующим образом:

[math]\displaystyle{ d(p, q) = \sqrt{\sum_{i=1}^n{(p_i - q_i)^2}} }[/math].

Теория чисел

Пифагорова тройка — набор из трёх натуральных чисел [math]\displaystyle{ (x,\;y,\;z) }[/math], которые могут быть длинами сторон прямоугольного треугольника, то есть натуральные числа, удовлетворяющие диофантову уравнению [math]\displaystyle{ x^2 + y^2 = z^2 }[/math]. Пифагоровы тройки играют важную роль в теории чисел, задача их эффективного нахождения породила широкий пласт работ, начиная с древнейших времён и вплоть до современности. Формулировка Великой теоремы Ферма аналогична задаче нахождения пифагоровых троек для степени более 2.

Единственная пифагорова тройка, состоящая из трёх последовательных чисел — это 3, 4 и 5: [math]\displaystyle{ 3^2+4^2=5^2 }[/math][31].

В массовой культуре

С одним из изображений доказательства теоремы связано популярное в русском школьном фольклоре выражение «Пифагоровы штаны на все стороны равны», получившее особенную известность благодаря комической опере 1915 года «Иванов Павел»[32][33].

Примечания

  1. ↑ Кантор ссылается на папирус 6619 Берлинского музея
  2. ↑ History topic: Pythagoras’s theorem in Babylonian mathematics. Дата обращения: 1 июня 2009. Архивировано 6 июня 2011 года.
  3. ↑ Наука, техническая и военная мысль, здравоохранение и образование // Духовная культура Китая: энциклопедия в 5 томах / Титаренко М. Л. — М.: Восточная литература РАН, 2009. — Т. 5. — С. 939—941. — 1055 с. — ISBN 9785020184299. Архивная копия от 4 марта 2016 на Wayback Machine
  4. ↑ Euclid, 1956, p. 351.
  5. ↑ Heath, 1921, vol I, p. 144.
  6. ↑ Kurt Von Fritz. The Discovery of Incommensurability by Hippasus of Metapontum (англ.) // The Annals of Mathematics, Second Series : journal. — Annals of Mathematics, 1945. — April (vol. 46, no. 2). — P. 242—264. — JSTOR 1969021.: «Принадлежит ли эта формула лично перу Пифагора…, но мы можем уверенно считать, что она принадлежит древнейшему периоду пифагорейской математики».
  7. ↑ Георг Гегель. Лекции по истории философии. — Litres, 2016-09-08. — С. 282. — 1762 с. — ISBN 9785457981690.
  8. ↑ Asger Aaboe. Episodes from the early history of mathematics (англ.). — Mathematical Association of America, 1997. — P. 51. — ISBN 0883856131. Архивная копия от 9 августа 2016 на Wayback Machine. — «…it is not until Euclid that we find a logical sequence of general theorems with proper proofs.».
  9. ↑ Elisha Scott Loomis. Pythagorean Proposition
  10. ↑ См. например Геометрия по Киселёву Архивная копия от 1 марта 2021 на Wayback Machine, § 196.
  11. ↑ См. например Геометрия по Киселёву Архивная копия от 1 марта 2021 на Wayback Machine, § 259.
  12. ↑ Franz Lemmermeyer. Leonardo da Vinci’s Proof of the Pythagorean Theorem (англ.). The College Mathematics Journal 47(5):361 (November 2016). Дата обращения: 22 октября 2021. Архивировано 7 июня 2022 года.
  13. ↑ См. например Геометрия по Киселёву Архивная копия от 1 марта 2021 на Wayback Machine, § 263.
  14. ↑ Euclid’s Elements: book VI, proposition VI 31: «In right-angled triangles the figure on the side subtending the right angle is equal to the similar and similarly described figures on the sides containing the right angle».
  15. ↑ Lawrence S. Leff. Cited work. — Barron's Educational Series, 2005. — С. 326. — ISBN 0764128922.
  16. ↑ Howard Whitley Eves. § 4.8: …generalization of Pythagorean theorem // Great moments in mathematics (before 1650) (англ.). — Mathematical Association of America, 1983. — P. 41. — ISBN 0883853108. Архивная копия от 9 августа 2016 на Wayback Machine
  17. ↑ Aydin Sayili. Thâbit ibn Qurra's Generalization of the Pythagorean Theorem (англ.) // Isis : journal. — 1960. — March (vol. 51, no. 1). — P. 35—37. — doi:10.1086/348837. — JSTOR 227603.
  18. ↑ Judith D. Sally, Paul Sally. Exercise 2.10 (II) // Cited work. — 2007. — С. 62. — ISBN 0821844032. Архивная копия от 9 августа 2016 на Wayback Machine
  19. ↑ George Jennings. Figure 1.32: The generalized Pythagorean theorem // Modern geometry with applications: with 150 figures (англ.). — 3rd. — Springer  (англ.) (рус., 1997. — P. 23. — ISBN 038794222X.
  20. ↑ Rajendra Bhatia. Matrix analysis. — Springer  (англ.) (рус., 1997. — С. 21. — ISBN 0387948465.
  21. ↑ Шилов Г. Е. Математический анализ. Специальный курс. — М.: Физматлит, 1961. — C. 194
  22. ↑ Stephen W. Hawking. Cited work. — 2005. — С. 4. — ISBN 0762419229. Архивная копия от 17 августа 2016 на Wayback Machine
  23. ↑ Eric W. Weisstein. CRC concise encyclopedia of mathematics. — 2nd. — 2003. — С. 2147. — ISBN 1584883472. Архивная копия от 17 августа 2016 на Wayback Machine. — «The parallel postulate is equivalent to the Equidistance postulate, Playfair axiom, Proclus axiom, the Triangle postulate and the Pythagorean theorem.».
  24. ↑ Alexander R. Pruss. The principle of sufficient reason: a reassessment (англ.). — Cambridge University Press, 2006. — P. 11. — ISBN 052185959X. Архивная копия от 9 августа 2016 на Wayback Machine. — «We could include… the parallel postulate and derive the Pythagorean theorem. Or we could instead make the Pythagorean theorem among the other axioms and derive the parallel postulate.».
  25. ↑ Victor Pambuccian. Maria Teresa Calapso’s Hyperbolic Pythagorean Theorem (англ.) // The Mathematical Intelligencer : journal. — 2010. — December (vol. 32). — P. 2. — doi:10.1007/s00283-010-9169-0.
  26. ↑ Barrett O'Neill. Exercise 4 // Elementary differential geometry. — 2nd. — Academic Press, 2006. — С. 441. — ISBN 0120887355.
  27. ↑ Saul Stahl. Theorem 8.3 // The Poincaré half-plane: a gateway to modern geometry (англ.). — Jones & Bartlett Learning  (англ.) (рус., 1993. — P. 122. — ISBN 086720298X.
  28. ↑ Микиша А. М., Орлов В. Б. Толковый математический словарь. Основные термины. — М. Русский язык, 1989 г.
  29. ↑ Jane Gilman. Hyperbolic triangles // Two-generator discrete subgroups of PSL (2, R) (англ.). — American Mathematical Society Bookstore, 1995. — ISBN 0821803611.
  30. ↑ Alfred Gray, Elsa Abbena, Simon Salamon. Modern differential geometry of curves and surfaces with Mathematica (англ.). — 3rd. — CRC Press, 2006. — P. 194. — ISBN 1584884487.
  31. ↑ Siegel E. This One Equation, 10² + 11² + 12² = 13² + 14², Takes Pythagoras To A Whole New Level (англ.). Forbes (6 марта 2020). Дата обращения: 28 апреля 2020. Архивировано 4 апреля 2020 года.
  32. ↑ Легендарная опера: текст и ноты. LiveJournal (4 августа 2016). Дата обращения: 9 января 2020. Архивировано 9 июня 2020 года.
  33. ↑ Словарь современных цитат. Litres, 20 мар. 2019 г. С. 9.

Литература

  • Ван-дер-Варден Б. Л. Пробуждающаяся наука. Математика Древнего Египта, Вавилона и Греции. — М., 1959.
  • Глейзер Г. И. История математики в школе. — М., 1982.
  • Еленьский Щ. По следам Пифагора. — М.: Детгиз, 1961. — 486 с. : ил., карт.
  • Клауди Альсина. Секта чисел. Теорема Пифагора. — М.: Де Агостини, 2014. — 152 с. — (Мир математики: в 45 томах, том 5). — ISBN 978-5-9774-0633-8.
  • Литцман В. Теорема Пифагора. — М., 1960.
    • Сайт о теореме Пифагора с большим числом доказательств, материал взят из книги В. Литцмана, большое число чертежей представлено в виде отдельных графических файлов.
  • Скопец З. А. Геометрические миниатюры. — М., 1990
  • Euclid. The Elements (3 vols.) / Translated by Johan Ludvig Heiberg with an introduction and commentary by Thomas L. Heath. — Reprint of 1908. — Dover, 1956. — Vol. 1 (Books I and II). — ISBN 0-486-60088-2.
  • Heath S. A History of Greek Mathematics (2 Vols.). — Edition of Dover Publications, Inc. (1981). — Clarendon Press, Oxford, 1921. — ISBN 0-486-24073-8.

Ссылки

Источник — https://xn--h1ajim.xn--p1ai/index.php?title=Теорема_Пифагора&oldid=10461259