Составное число

Натуральные числа от нуля до ста. Составные числа отмечены зелёным.

Составно́е число́ — натуральное число, имеющее делители, отличные от единицы и самого себя. Каждое составное число является произведением двух или более натуральных чисел, бо́льших единицы. Все натуральные числа делятся на три непересекающиеся категории: простые, составные и единица.

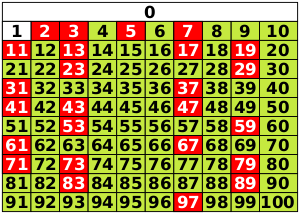
Начало последовательности составных чисел (A002808)::

4, 6, 8, 9, 10, 12, 14, 15, 16, 18, 20, 21, 22, 24, 25, 26, 27, 28, 30, 32, 33, 34, 35, 36, 38, 39, 40, 42, 44, 45, 46, 48, 49, 50, 51, 52, 54, 55, 56, 57, 58, 60, 62, 63, 64, 65, 66, 68, 69, 70, 72, 74, 75, 76, 77, 78, 80, 81, 82, 84, 85, 86, 87, 88, 90, 91, 92, 93, 94, 95, 96, 98, 99, 100, ...

Связанные понятия

Каждое натуральное число, большее единицы, имеет по крайней мере два делителя, которые называются тривиальными: единицу и самого себя. Число является составным, если оно имеет нетривиальные делители.

Составное натуральное число называется:

• полупростым, если его можно представить в виде произведения двух простых чисел (не обязательно различных);
• сфеническим, если его можно представить в виде произведения трёх простых чисел (не обязательно различных);
• полнократным, если его можно представить в виде произведения [math]\displaystyle{ a^2b^3, }[/math] где [math]\displaystyle{ a,b }[/math] — натуральные числа. Равносильное определение: число [math]\displaystyle{ N }[/math] полнократно, если для любого его простого делителя [math]\displaystyle{ p }[/math] число [math]\displaystyle{ p^2 }[/math] также является делителем [math]\displaystyle{ N }[/math];
• сверхсоставным, если у него больше делителей, чем у любого меньшего числа (два первых сверхсоставных числа не являются составными, это 1 и 2).

Свойства

Основная теорема арифметики утверждает, что любое составное число может быть разложено в произведение простых множителей, причём единственным способом (с точностью до порядка множителей).

Покажем, что в натуральном ряду можно найти последовательности подряд идущих составных чисел любой длины. Пусть n — произвольное натуральное число. Обозначим:

[math]\displaystyle{ N=(n+1)! = 1 \cdot 2 \cdot 3 \cdot 4 \dots \cdot (n+1). }[/math]

Тогда n последовательных чисел [math]\displaystyle{ N+2, N+3, N+4 \dots N+(n+1) }[/math] содержит только составные числа: [math]\displaystyle{ N+2 }[/math] делится на 2, [math]\displaystyle{ N+3 }[/math] делится на 3 и т. д.

Разложение числа на множители

Чтобы определить, является ли заданное натуральное число [math]\displaystyle{ N }[/math] простым или составным, надо найти его нетривиальные делители или доказать, что таких не существует. В случае небольшого [math]\displaystyle{ N }[/math] поиск его делителей — несложная задача, для этого можно использовать признаки делимости или специальные алгоритмы, указанные в статьях Тест простоты и Факторизация целых чисел. Нахождение делителей больших чисел (актуальная задача криптографии) может оказаться проблемой, превышающей возможности современных компьютеров.

Вариации и обобщения

Понятия простого и составного числа можно определить не только для натуральных чисел, но и для других алгебраических структур; чаще всего рассматриваются коммутативные кольца без делителей нуля (области целостности).

Пример 1. Кольцо целых чисел содержит два делителя единицы (обратимых элемента): [math]\displaystyle{ +1 }[/math] и [math]\displaystyle{ -1. }[/math] Поэтому все целые числа, за исключением делителей единицы, имеют не два, а по меньшей мере четыре тривиальных делителя; например, у числа 7 делителями являются [math]\displaystyle{ 1; 7; -1; -7. }[/math] В связи с этим формулировку основной теорему арифметики необходимо скорректировать: любое составное число может быть разложено в произведение простых множителей, причём единственным способом, с точностью до порядка множителей и делителей единицы.

Простые целые числа, как и прежде — это те, у которых нет нетривиальных делителей. Таким образом, кольцо целых чисел делится на три непересекающиеся части: простые, составные и делители единицы.

Пример 2. Кольцо гауссовых целых чисел образовано комплексными числами [math]\displaystyle{ a+bi, }[/math] у которых [math]\displaystyle{ a,b }[/math] — обычные целые числа. Для чисел такого вида можно определить деление нацело по общим правилам. Делителей единицы здесь четыре: [math]\displaystyle{ 1; -1; i; -i. }[/math]

Простые гауссовы числа — это часть обычных простых чисел и «простые гауссовы» (например, [math]\displaystyle{ 1+i }[/math]). См. критерий простоты гауссова числа. Простое натуральное число может не быть простым гауссовым; например, число 5 как гауссово число является составным: [math]\displaystyle{ 5 = (2+i)(2-i). }[/math] Основная теорема арифметики формулируется точно так же, как указано выше для целых чисел.

Пример 3. Кольцо многочленов [math]\displaystyle{ R[x] }[/math] образовано многочленами с вещественными коэффициентами. Делителями единицы являются здесь ненулевые числовые константы (рассматриваемые как многочлены нулевой степени). Аналогами простых чисел здесь будут все неразложимые (неприводимые) многочлены, то есть многочлены 1-й степени и те многочлены 2-й степени, у которых нет вещественных корней (потому что их дискриминант отрицателен). Следовательно, аналогом составных чисел выступают все многочлены степени больше второй, а также многочлены второй степени с неотрицательным дискриминантом. И здесь основная теорема арифметики имеет место и формулируется точно так же, как указано выше для целых чисел.

Литература

• Зайцев В. В., Рыжков В. В., Сканави М. И. Элементарная математика. Повторительный курс. — Издание третье, стереотипное. — М.: Наука, 1976. — 591 с.
• Составное число // Большая российская энциклопедия [Электронный ресурс]. — 2004—2017.

Ссылки

• Списки простых и факторизованных составных чисел