Распределение Пуассона
| Распределение Пуассона | |
|---|---|
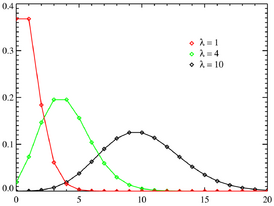 Функция вероятности Функция вероятности | |
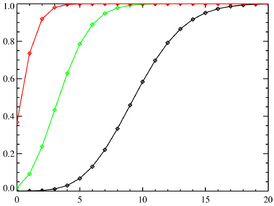 Функция распределения Функция распределения | |
| Обозначение | [math]\displaystyle{ \mathrm{P}(\lambda) }[/math] |
| Параметры | [math]\displaystyle{ \lambda \in (0,\infty) }[/math] |
| Носитель | [math]\displaystyle{ k \in \{0,1,2,\ldots\} }[/math] |
| Функция вероятности | [math]\displaystyle{ \frac{e^{-\lambda} \lambda^k}{k!} }[/math] |
| Функция распределения | [math]\displaystyle{ \frac{\Gamma(k+1, \lambda)}{k!} }[/math] |
| Математическое ожидание | [math]\displaystyle{ \lambda }[/math] |
| Медиана | [math]\displaystyle{ \approx\lfloor\lambda+1/3-0.02/\lambda\rfloor }[/math] |
| Мода | [math]\displaystyle{ \lfloor\lambda\rfloor }[/math] |
| Дисперсия | [math]\displaystyle{ \lambda }[/math] |
| Коэффициент эксцесса | [math]\displaystyle{ \lambda^{-1} }[/math] |
| Дифференциальная энтропия | [math]\displaystyle{ \lambda[1\!-\!\ln(\lambda)]\!+\!e^{-\lambda}\sum_{k=0}^\infty \frac{\lambda^k\ln(k!)}{k!} }[/math] |
| Производящая функция моментов | [math]\displaystyle{ \exp(\lambda (e^t-1)) }[/math] |
| Характеристическая функция | [math]\displaystyle{ \exp(\lambda (e^{it}-1)) }[/math] |
Распределе́ние Пуассо́на — распределение дискретного типа случайной величины, представляющей собой число событий, произошедших за фиксированное время, при условии, что данные события происходят с некоторой фиксированной средней интенсивностью и независимо друг от друга.
Распределение Пуассона играет ключевую роль в теории массового обслуживания.
Определение
При распределении вероятностей Пуассона с математическим ожиданием [math]\displaystyle{ \lambda }[/math] событий в данном интервале (плоскости, пространстве) вероятность [math]\displaystyle{ k }[/math] событий в том же интервале (плоскости, пространстве) будет равна:
- [math]\displaystyle{ \frac{\lambda^k e^{-\lambda}}{k!} . }[/math]
Выберем фиксированное число [math]\displaystyle{ \lambda \gt 0 }[/math] и определим дискретное распределение, задаваемое следующей функцией вероятности - теоремой Пуассона:
- [math]\displaystyle{ p(k) \equiv \mathbb{P}(Y=k) = \frac{\lambda^k}{k!}\, e^{-\lambda} }[/math],
где
- [math]\displaystyle{ k }[/math] — количество событий,
- [math]\displaystyle{ \lambda }[/math] — математическое ожидание случайной величины (среднее количество событий за фиксированный промежуток времени),
- [math]\displaystyle{ k! }[/math] обозначает факториал числа [math]\displaystyle{ k }[/math],
- [math]\displaystyle{ e = 2{,}718281828\ldots }[/math] — основание натурального логарифма.
Тот факт, что случайная величина [math]\displaystyle{ Y }[/math] имеет распределение Пуассона с математическим ожиданием [math]\displaystyle{ \lambda }[/math], записывается: [math]\displaystyle{ Y \sim~ \mathrm{P}(\lambda) }[/math].
Моменты
Производящая функция моментов распределения Пуассона имеет вид:
- [math]\displaystyle{ E_Y(t)=e^{\lambda\left(e^t-1\right)} }[/math],
откуда
- [math]\displaystyle{ \mathbb{M}[Y]=\lambda }[/math],
- [math]\displaystyle{ \mathbb{D}[Y]=\lambda }[/math].
Для факториальных моментов распределения справедлива общая формула:
- [math]\displaystyle{ \mathbb{M}Y^{[k]}= \sum_{i=0}^k \lambda^i \left\{\begin{matrix} k \\ i \end{matrix}\right\} }[/math],
где [math]\displaystyle{ k=1,2,... }[/math] Фигурные же скобки обозначают Числа Стирлинга второго рода.
А так как моменты и факториальные моменты линейным образом связаны, то часто для пуассоновского распределения исследуются именно факториальные моменты, из которых при необходимости можно вывести и обычные моменты.
Свойства распределения Пуассона
- Сумма независимых пуассоновских случайных величин также имеет распределение Пуассона. Пусть [math]\displaystyle{ Y_i\sim\mathrm{P}(\lambda_i),\; i=1,\ldots,n }[/math]. Тогда
- [math]\displaystyle{ Y = \sum\limits_{i=1}^n Y_i \sim \mathrm{P}\left(\sum\limits_{i=1}^n \lambda_i\right) }[/math].
- Пусть [math]\displaystyle{ Y_i \sim \mathrm{P}(\lambda_i),\; i=1,2 }[/math], и [math]\displaystyle{ Y = Y_1 + Y_2 }[/math]. Тогда условное распределение [math]\displaystyle{ Y_1 }[/math] при условии, что [math]\displaystyle{ Y = y }[/math], биномиально. Более точно:
- [math]\displaystyle{ Y_1\mid Y = y \sim \mathrm{Bin}\left(y, \frac{\lambda_1}{\lambda_1+\lambda_2}\right) }[/math].
- C увеличением [math]\displaystyle{ \lambda }[/math] распределение Пуассона стремится к распределению Гаусса со среднеквадратичным отклонением [math]\displaystyle{ \sigma=\sqrt{\lambda} }[/math] и сдвигом [math]\displaystyle{ \lambda }[/math]. Чтобы доказать это, нужно применить формулу Стирлинга для факториала, а затем воспользоваться разложением в ряд Тейлора [math]\displaystyle{ \ln(\lambda/k)^k }[/math] в окрестности [math]\displaystyle{ k=\lambda }[/math] и тем, что в пределах пика распределения [math]\displaystyle{ \sqrt{k}\approx\sqrt{\lambda} }[/math]. Тогда получается
- [math]\displaystyle{ p(k)\approx\frac{1}{\sqrt{2\pi\lambda}}\exp\left(-\frac{(k-\lambda)^2}{2\lambda}\right) }[/math]
Асимптотическое стремление к распределению
Довольно часто в теории вероятностей рассматривают не само распределение Пуассона, а последовательность распределений, асимптотически равных ему. Более формально, рассматривают последовательность случайных величин [math]\displaystyle{ \xi_1, \xi_2, \dots }[/math], принимающих целочисленные значения, такую что для всякого [math]\displaystyle{ k }[/math] выполнено [math]\displaystyle{ P\{\xi_n=k\} \sim \frac{\lambda^k e^{-\lambda}}{k!} }[/math] при [math]\displaystyle{ n \to \infty }[/math].
Простейшим примером является случай, когда [math]\displaystyle{ \xi_n }[/math] имеет биномиальное распределение с вероятностью успеха [math]\displaystyle{ \frac{\lambda}{n} }[/math] в каждом из [math]\displaystyle{ n }[/math] испытаний.
Обратная связь с факториальными моментами
Рассмотрим последовательность случайных величин [math]\displaystyle{ \xi_1, \xi_2, \dots, }[/math] принимающих целые неотрицательные значения. Если [math]\displaystyle{ \mu_r({\xi_n}) \sim \lambda^r }[/math] при [math]\displaystyle{ n \to \infty }[/math] и любом фиксированном [math]\displaystyle{ r }[/math] (где [math]\displaystyle{ \mu_r({\xi_n}) }[/math] — [math]\displaystyle{ r }[/math]-й факториальный момент), то для всякого [math]\displaystyle{ k }[/math] при [math]\displaystyle{ n \to \infty }[/math] выполнено [math]\displaystyle{ P\{\xi_n=k\} \sim \frac{\lambda^k e^{-\lambda}}{k!} }[/math].
Лемма
Для начала докажем общую формулу вычисления вероятности появления конкретного значения случайной величины через факториальные моменты. Пусть для некоторого [math]\displaystyle{ \xi }[/math] известны все [math]\displaystyle{ \mu_r(\xi) }[/math] и [math]\displaystyle{ \mu_r(\xi) \to 0 }[/math] при [math]\displaystyle{ r \to \infty }[/math]. Тогда
[math]\displaystyle{ \sum \limits_{r=k}^{\infty} {(-1)^{r-k} \frac{\mu_r(\xi)}{k!(r-k)!}} = \sum \limits_{r=k}^{\infty} {\sum \limits_{s=r}^{\infty} {(-1)^{r-k} \frac{s!}{k!(r-k)!(s-r)!} P\{\xi=s\}}}. }[/math]
Изменяя порядок суммирования, это выражение можно преобразовать в
[math]\displaystyle{ \sum \limits_{s=k}^{\infty} {P\{\xi=s\} \sum \limits_{r=k}^{s} {\frac{(-1)^{r-k} s!}{k!(r-k)!(s-r)!}}} = \sum \limits_{s=k}^{\infty} {P\{\xi=s\} \frac{s!}{k!} \sum_{t=0}^{s-k} {\frac{(-1)^t}{t!((s-k)-t)!}}}. }[/math]
Далее, из известной формулы [math]\displaystyle{ \sum \limits_{k=0}^{n} {(-1)^k C_n^k}=0 }[/math] получаем, что [math]\displaystyle{ \frac{s!}{k!} \sum_{t=0}^{s-k} {\frac{(-1)^t}{t!((s-k)-t)!}} = 0 }[/math] при [math]\displaystyle{ s\gt k }[/math] и то же выражение вырождается в [math]\displaystyle{ 1 }[/math] при [math]\displaystyle{ s=k }[/math].
Тем самым доказано, что [math]\displaystyle{ P\{\xi=k\} = \sum \limits_{r=k}^{\infty} {(-1)^{r-k} \frac{\mu_r(\xi)}{k!(r-k)!}}. }[/math]
Доказательство теоремы
Согласно лемме и условиям теоремы, [math]\displaystyle{ P\{\xi_n=k\} \sim \sum \limits_{r=k}^{\infty} {(-1)^{r-k} \frac{\lambda^r}{k!(r-k)!}} = \sum \limits_{r=0}^{\infty} {(-1)^r \frac{\lambda^{r+k}}{k!r!}} = \frac{\lambda^k}{k!} \sum \limits_{r=0}^{\infty} {\frac{(-\lambda)^r}{r!}} = \frac{\lambda^k e^{-\lambda}}{k!} }[/math] при [math]\displaystyle{ n \to \infty }[/math].
Как пример нетривиального следствия этой теоремы можно привести, например, асимптотическое стремление к [math]\displaystyle{ \mathrm{P}(\lambda) }[/math] распределения количества изолированных рёбер (двухвершинных компонент связности) в случайном [math]\displaystyle{ n }[/math]-вершинном графе, где каждое из рёбер включается в граф с вероятностью [math]\displaystyle{ p_n \sim \frac{2\lambda}{n^2} }[/math].[1]
История
Работа Симеона Дени Пуассона «Исследования о вероятности приговоров в уголовных и гражданских делах»[2], в которой было введено данное распределение, была опубликована в 1837 году[3]. Примеры других ситуаций, которые можно смоделировать, применив это распределение: поломки оборудования, длительность исполнения ремонтных работ стабильно работающим сотрудником, ошибка печати, рост колонии бактерий в чашке Петри, дефекты в длинной ленте или цепи, импульсы счётчика радиоактивного излучения, количество забиваемых футбольной командой голов и др.[4]
См. также
Примечания
- ↑ Видеолекция Школы Анализа Данных. Дата обращения: 7 декабря 2014. Архивировано 8 апреля 2014 года.
- ↑ Пуассон, 1837.
- ↑ Чукова Ю. П. Распределение Пуассона // «Квант» : науч.-поп. физ.-мат. журн. — М.: «Наука», 1988. — № 8. — С. 15‒18. — ISSN 0130-2221.
- ↑ Винс, 2012, с. 370.
Литература
- Вентцель Е. С., Овчаров Л. А. Теория вероятностей и её инженерные приложения. 2-е изд. — М.: Высшая школа, 2000. — 480 с. — ISBN 978-5-406-00565-1. — С. 135.
- Винс, Ральф. Математика управления капиталом: Методы анализа риска для трейдеров и портфельных менеджеров = The mathematics of money management risk analysis techniques for traders. — М.: Альпина Паблишер, 2012. — 400 с. — ISBN 978-5-9614-1894-1.
- Пуассон С. Д. Исследования о вероятности приговоров в уголовных и гражданских делах = Poisson S.-D. Recherches sur la probabilité des jugements en matière criminelle et en matière civile. — Berlin: NG Verlag (Viatcheslav Demidov Inhaber), 2013. — 330 p. — ISBN 978-3-942944-29-8. [Poisson.pdf]. Архивировано 1 ноября 2014 года.
- Guerriero V. Power Law Distribution: Method of Multi-scale Inferential Statistics. — Journal of Modern Mathematics Frontier, 2012, 1. — P. 21—28. Архивная копия от 21 февраля 2018 на Wayback Machine
Ссылки
Для улучшения этой статьи по математике желательно: |