Распределение Вейбулла
| Распределение Вейбулла | |
|---|---|
 Плотность вероятности Плотность вероятности | |
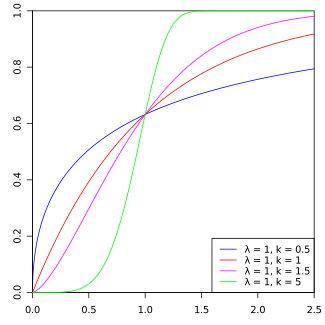 Функция распределения Функция распределения | |
| Обозначение | [math]\displaystyle{ \mathrm{W}(k,\lambda) }[/math] |
| Параметры |
[math]\displaystyle{ \lambda\gt 0 }[/math] - коэффициент масштаба, [math]\displaystyle{ k\gt 0 }[/math] - коэффициент формы |
| Носитель | [math]\displaystyle{ x \in [0; +\infty) }[/math] |
| Плотность вероятности | [math]\displaystyle{ (k/\lambda) (x/\lambda)^{(k-1)} e^{-(x/\lambda)^k} }[/math] |
| Функция распределения | [math]\displaystyle{ 1- e^{-(x/\lambda)^k} }[/math] |
| Математическое ожидание | [math]\displaystyle{ \lambda \Gamma\left(1+\frac{1}{k}\right) }[/math] |
| Медиана | [math]\displaystyle{ \lambda(\ln2)^{1/k}\, }[/math] |
| Мода | [math]\displaystyle{ \frac{\lambda(k-1)^{\frac{1}{k}}}{k^{\frac{1}{k}}}, }[/math] для [math]\displaystyle{ k\gt 1 }[/math] |
| Дисперсия | [math]\displaystyle{ \lambda^2\Gamma\left(1+\frac{2}{k}\right) - \mu^2 }[/math] |
| Коэффициент асимметрии | [math]\displaystyle{ \frac{\Gamma(1+\frac{3}{k})\lambda^3-3\mu\Gamma(1+\frac{2}{k})\lambda^2+2\mu^3}{\sigma^3} }[/math] |
| Коэффициент эксцесса | [math]\displaystyle{ \frac{\lambda^4\Gamma\left(1+\frac4k\right)-4\lambda^3\mu\Gamma\left(1+\frac3k\right)+ 6\lambda^2\mu^2\Gamma\left(1+\frac2k\right)-3\mu^4}{\sigma^4} }[/math] |
| Дифференциальная энтропия | [math]\displaystyle{ \gamma\left(1\!-\!\frac{1}{k}\right)+\ln\left(\frac{\lambda}{k}\right)+1 }[/math] |
| Производящая функция моментов | [math]\displaystyle{ \sum_{n=0}^\infty \frac{t^n\lambda^n}{n!}\Gamma(1+n/k), \ k\geq1 }[/math] |
| Характеристическая функция | [math]\displaystyle{ \sum_{n=0}^\infty \frac{(it)^n\lambda^n}{n!}\Gamma(1+n/k) }[/math] |
Распределе́ние Ве́йбулла в теории вероятностей — двухпараметрическое семейство абсолютно непрерывных распределений. Названо в честь Валодди Вейбулла, детально охарактеризовавшего его в 1951, хотя впервые его определил Фреше в 1927, а применено оно было ещё в 1933 для описания распределения размеров частиц.
Определение
Пусть распределение случайной величины [math]\displaystyle{ X }[/math] задаётся плотностью [math]\displaystyle{ f_X(x) }[/math], имеющей вид:
- [math]\displaystyle{ f_X(x) = \left\{ \begin{matrix} \frac{k}{\lambda} \left(\frac{x}{\lambda}\right)^{k-1} e^{-\left(\frac{x}{\lambda}\right)^k}, & x \ge 0 \\ 0, & x \lt 0 \end{matrix} \right.. }[/math]
Тогда говорят, что [math]\displaystyle{ X }[/math] имеет распределение Вейбулла. Пишут: [math]\displaystyle{ X \sim \mathrm{W}(k,\lambda) }[/math].
Если величину X принять за наработку до отказа, тогда получается распределение, в котором интенсивность отказов пропорциональна времени. Тогда:
- k < 1 показывает, что интенсивность отказов уменьшается со временем
- k = 1 показывает, что интенсивность отказов не меняется со временем
- k > 1 показывает, что интенсивность отказов увеличивается со временем
В материаловедении коэффициент k известен как модуль Вейбулла.
Свойства
Функция плотности
Вид функции плотности распределения Вейбулла сильно зависит от значения k. Для 0 < k < 1 плотность стремится к бесконечности при [math]\displaystyle{ x\to 0+ }[/math] и строго убывает. Для k = 1 плотность стремится к 1/λ при [math]\displaystyle{ x\to 0+ }[/math] и строго убывает. Для k > 1 плотность стремится к 0 при [math]\displaystyle{ x\to 0+ }[/math], возрастает до достижения своей моды и убывает после. Плотность имеет бесконечный отрицательный угловой коэффициент в x = 0 при 0 < k < 1 , бесконечный положительный угловой коэффициент в x = 0 при 1 < k < 2, и нулевой угловой коэффициент в x = 0 при k > 2. При k = 2 плотность имеет конечный положительный угловой коэффициент в x = 0. При [math]\displaystyle{ k\to \infty }[/math] распределение Вейбулла сходится к дельта-функции, центрированной в x = λ. Кроме того, коэффициент асимметрии и коэффициент вариации зависят только от коэффициента формы.
Функция распределения
Функция распределения Вейбулла:
- [math]\displaystyle{ F(x;k,\lambda) = 1- e^{-(x/\lambda)^k} }[/math]
при x ≥ 0, и F(x; k; λ) = 0 при x < 0
Квантиль распределения Вейбулла:
- [math]\displaystyle{ Q(p;k,\lambda) = \lambda {(-\ln(1-p))}^{1/k} }[/math]
при 0 ≤ p < 1.
Интенсивность отказов h:
- [math]\displaystyle{ h(x;k,\lambda) = {k \over \lambda} \left({x \over \lambda}\right)^{k-1}. }[/math]
Моменты
Производящая функция моментов логарифма случайной величины, имеющей распределение Вейбулла
- [math]\displaystyle{ \mathbb{E}\left[e^{t\log X}\right] = \lambda^t\Gamma\left(\frac{t}{k}+1\right), }[/math]
где Γ — это гамма-функция. Аналогично, Характеристическая функция логарифма X задаётся
- [math]\displaystyle{ \mathbb{E}\left[e^{it\log X}\right] = \lambda^{it}\Gamma\left(\frac{it}{k}+1\right). }[/math]
Моменты случайной величины [math]\displaystyle{ X }[/math], имеющей распределение Вейбулла имеют вид
- [math]\displaystyle{ \mathbb{E}\left[X^n\right] = \lambda^n \Gamma\left(1 + \frac{n}{k}\right) }[/math], где [math]\displaystyle{ \Gamma }[/math] — гамма-функция,
откуда
- [math]\displaystyle{ \mathbb{E}[X] = \lambda \Gamma\left(1 + \frac{1}{k}\right) }[/math],
- [math]\displaystyle{ \mathrm{D}[X] = \lambda^2 \left[\Gamma\left(1 + \frac{2}{k}\right) - \Gamma^2\left(1 + \frac{1}{k}\right)\right] }[/math].
Коэффициент асимметрии задаётся функцией
- [math]\displaystyle{ \gamma_1=\frac{\Gamma\left(1+\frac{3}{k}\right)\lambda^3-3\mu\sigma^2-\mu^3}{\sigma^3} }[/math]
- [math]\displaystyle{ \gamma_2=\frac{-6\Gamma_1^4+12\Gamma_1^2\Gamma_2-3\Gamma_2^2 -4\Gamma_1\Gamma_3+\Gamma_4}{[\Gamma_2-\Gamma_1^2]^2}, }[/math]
где [math]\displaystyle{ \Gamma_i=\Gamma(1+i/k) }[/math], так же может быть записан:
- [math]\displaystyle{ \gamma_{2}=\frac{\lambda^4\Gamma(1+\frac{4}{k})-4\gamma_{1}\sigma^3\mu-6\mu^2\sigma^2-\mu^4}{\sigma^4}-3 }[/math]
Производящая функция моментов
Существует множество выражений для производящей функции моментов самой [math]\displaystyle{ X }[/math]
- [math]\displaystyle{ \mathbb{E}\left[e^{tX}\right] = \sum_{n=0}^\infty \frac{t^n\lambda^n}{n!}\Gamma\left(1+\frac{n}{k}\right). }[/math]
Так же можно работать непосредственно с интегралом
- [math]\displaystyle{ \mathbb{E}\left[e^{tX}\right] = \int_0^\infty e^{tx} \frac{k}{\lambda}\left(\frac{x}{\lambda}\right)^{k-1}e^{-(x/\lambda)^k}\,dx. }[/math]
Если коэффициент k предполагается рациональным числом, выраженным k = p/q, где p и q целые, то интеграл может быть вычислен аналитически.[1] С заменой t на -t, получается
- [math]\displaystyle{ \mathbb{E}\left[e^{-tX}\right] = \frac1{ \lambda^k\, t^k} \, \frac{ p^k \, \sqrt{q/p}} {(\sqrt{2 \pi})^{q+p-2}} \, G_{p,q}^{\,q,p} \!\left( \left. \begin{matrix} \frac{1-k}{p}, \frac{2-k}{p}, \dots, \frac{p-k}{p} \\ \frac{0}{q}, \frac{1}{q}, \dots, \frac{q-1}{q} \end{matrix} \; \right| \, \frac {p^p} {\left( q \, \lambda^k \, t^k \right)^q} \right), }[/math]
где G — это G-функция Мейера.
Информационная энтропия
Информационная энтропия задаётся таким образом
- [math]\displaystyle{ H(\lambda,k) = \gamma\left(1\!-\!\frac{1}{k}\right) + \ln\left(\frac{\lambda}{k}\right) + 1, }[/math]
где [math]\displaystyle{ \gamma }[/math] — это Постоянная Эйлера — Маскерони.
Оценка коэффициентов
Наибольшее правдоподобие
Оценка максимального правдоподобия для коэффициента [math]\displaystyle{ \lambda }[/math]
- [math]\displaystyle{ \hat \lambda^k = \frac{1}{n} \sum_{i=1}^n x_i^k }[/math]
Для [math]\displaystyle{ k }[/math]
- [math]\displaystyle{ \hat k^{-1} = \frac{\sum_{i=1}^n x_i^k \ln x_i } {\sum_{i=1}^n x_i^k } - \frac{1}{n} \sum_{i=1}^n \ln x_i }[/math]
Условная функция надёжности Вейбулла
Для 2-х параметрического распределения Вейбулла функция имеет вид:
- [math]\displaystyle{ R(t|T)={ \frac{R(T+t)}{R(T)}}={\frac{e^{-\left( {\frac{T+t }{\lambda }}\right) ^{k }}}{e^{-\left( {\frac{T }{\lambda }}\right) ^{k }}}} }[/math]
- или
- [math]\displaystyle{ R(t|T)=e^{-\left[ \left( {\frac{T+t }{\lambda }}\right) ^{k }-\left( {\frac{T}{\lambda }}\right) ^{k }\right] } }[/math]
Для 3-х параметрического:
- [math]\displaystyle{ R(t|T)={ \frac{R(T+t)}{R(T)}}={\frac{e^{-\left( {\frac{T+t-\theta }{\lambda }}\right) ^{k }}}{e^{-\left( {\frac{T-\theta }{\lambda }}\right) ^{k }}}} }[/math]
Она называется условной, потому что показывает вероятность того, что объект проработает ещё [math]\displaystyle{ t }[/math] времени при условии, что он уже проработал [math]\displaystyle{ T }[/math].
График Вейбулла
Данные распределения Вейбулла визуально могут быть оценены с использованием графика Вейбулла[2] . Это график типа Q-Q выборочной функции распределения со специальными осями. Оси — [math]\displaystyle{ \ln(-\ln(1-\hat F(x))) }[/math] и [math]\displaystyle{ \ln(x) }[/math] Причина изменения переменных в том, что выборочная функция распределения Вейбулла может быть представлена в линейном виде
- [math]\displaystyle{ \begin{align} F(x) &= 1-e^{-(x/\lambda)^k}\\ -\ln(1-F(x)) &= (x/\lambda)^k\\ \underbrace{\ln(-\ln(1-F(x)))}_{\textrm{'y'}} &= \underbrace{k\ln x}_{\textrm{'mx'}} - \underbrace{k\ln \lambda}_{\textrm{'c'}} \end{align} }[/math]
Поэтому если данные получены из распределения Вейбулла, на графике Вейбулла можно ожидать прямую линию.
Есть множество способов получения выборочной функции распределения из данных: один из методов заключается в том, чтобы получить вертикальную координату каждой точки, используя [math]\displaystyle{ \hat F = \frac{i-0.3}{n+0.4} }[/math], где [math]\displaystyle{ i }[/math] — это ранг точки данных, а [math]\displaystyle{ n }[/math] — это общее количество точек.[3]
Использование
Распределение Вейбулла используется:
- В анализе выживаемости
- В надёжности и анализе отказов
- В электротехнике для представления перенапряжения, возникающего в электрических цепях
- В промышленной инженерии
- В теории экстремальных значений
- В прогнозировании погоды
- Для описания распределения скорости ветра как распределения, обычно совпадающего с распределением Вейбулла в ветроэнергетике
- В радиолокационных системах для моделирования дисперсии уровня принимаемого сигналов, создаваемой некоторыми типами клаттеров
- В моделировании замирания сигнала в беспроводных коммуникациях
- В прогнозировании технологических изменений
- В гидрологии распределение Вейбулла применимо к экстремальным событиям, таким как выпадение годовой нормы дождей за день или разливу реки. На рисунке показано такое соответствие, а также 90 % доверительный интервал, основанный на биномиальном распределении.
- В описании размера частиц, полученных путём размельчения, помола или дробления
- Из-за доступности используется в электронных таблицах, когда основное поведение в действительности лучше описывается распределением Эрланга
Связь с другими распределениями
- Обычное распределение Вейбулла заменой переменной сводится к гамма-распределению.
- 3-параметрическое распределение Вейбулла. Имеет функцию плотности
- [math]\displaystyle{ f(x;k,\lambda, \theta)={k \over \lambda} \left({x - \theta \over \lambda}\right)^{k-1} e^{-({x-\theta \over \lambda})^k} }[/math]
где [math]\displaystyle{ x \geq \theta }[/math] и f(x; k, λ, θ) = 0 при x < θ, где [math]\displaystyle{ k \gt 0 }[/math] — коэффициент формы, [math]\displaystyle{ \lambda \gt 0 }[/math] — коэффициент масштаба и [math]\displaystyle{ \theta }[/math] — коэффициент сдвига распределения. Когда θ=0, оно сводится к 2-х параметрическому распределению Вейбулла.
- 1-параметрическое распределение Вейбулла. Выводится предполагая [math]\displaystyle{ \theta=0 }[/math] и [math]\displaystyle{ k=C=Constant }[/math]:
- [math]\displaystyle{ f(t)={ \frac{C}{\lambda }}\left( {\frac{t}{\lambda }}\right) ^{C-1}e^{-\left( {\frac{t}{ \lambda }}\right) ^{C}} }[/math]
- Распределение Вейбулла может быть получено как функция от экспоненциального.
Если [math]\displaystyle{ X }[/math] — экспоненциальное распределение [math]\displaystyle{ \operatorname{Exp}(\lambda) }[/math] для параметра [math]\displaystyle{ \lambda }[/math], то случайная величина [math]\displaystyle{ Y = X^{1/k} ~(k\gt 0) }[/math] имеет распределение Вейбулла [math]\displaystyle{ \operatorname{W}(\lambda^{1/k}, k) }[/math]. Для доказательства рассмотрим функцию распределения [math]\displaystyle{ Y }[/math]:
[math]\displaystyle{ F_Y(y) = P(Y \le y) = P(X^{1/k} \le y) = P(X \le y^k) = 1 - e^{-\lambda \cdot y^k} = 1 - e^{-(\lambda^{1/k} \cdot y)^k},~y \gt 0 }[/math]
Полученная функция — функция распределения для распределения Вейбулла.
- Метод обратного преобразования: если [math]\displaystyle{ U \sim \mathrm{U}(0,1) }[/math], то
- [math]\displaystyle{ \lambda \left(-\ln U\right)^{1/k} \sim \mathrm{W}(k,\lambda) }[/math].
- С распределением Фреше: если [math]\displaystyle{ \mathrm{X} \sim \textrm{Weibull}(k = \alpha, \lambda = m) }[/math] , то [math]\displaystyle{ \tfrac{m^2}{\mathrm{X}} \sim \textrm{Frechet}(\alpha, s, m) }[/math].
- С распределением Гумбеля: если [math]\displaystyle{ \mathrm{X} \sim \textrm{Weibull} }[/math] , то [math]\displaystyle{ \log (X) \sim \textrm{Gumbel} }[/math].
- Распределение Рэлея — частный случай распределения Вейбулла при [math]\displaystyle{ k = 2 }[/math] и [math]\displaystyle{ \lambda = \sqrt{2}\sigma }[/math][4]
- Распределение Вейбулла является частным случаем обобщённого распределения экстремальных значений[5]
- Впервые распределение Вейбулла было применено для описания распределения размера частиц. Широко использовалось в обогащении полезных ископаемых при измельчении. В этом контексте
функция распределения имеет вид
- [math]\displaystyle{ f(x;P_{\rm{80}},m) = \begin{cases} 1-e^{ln\left(0.2\right)\left(\frac{x}{P_{\rm{80}}}\right)^m} & x\geq0 ,\\ 0 & x\lt 0 ,\end{cases} }[/math]
где
- [math]\displaystyle{ x }[/math]: Размер частицы
- [math]\displaystyle{ P_{\rm{80}} }[/math]: 80-й процентиль распределения размера частиц
- [math]\displaystyle{ m }[/math]: Коэффициент, описывающий размах распределения
Примечания
- ↑ См. (Cheng, Tellambura & Beaulieu 2004) для случая целого k, и (Sagias & Karagiannidis 2005) в случае рационального.
- ↑ график Вейбулла. Дата обращения: 20 сентября 2015. Архивировано 25 марта 2008 года.
- ↑ Wayne Nelson (2004) Applied Life Data Analysis. Wiley-Blackwell ISBN 0-471-64462-5
- ↑ Rayleigh Distribution — MATLAB & Simulink — MathWorks Australia. Дата обращения: 21 сентября 2015. Архивировано 12 октября 2014 года.
- ↑ Всемирная Метеорологическая Организация. Руководство по гидрологической практике. — 6. — Швейцария, 2012. — Т. 2. — С. 165. — ISBN 978-92-63-40168-7..
Литература
- Fréchet, Maurice (1927), Sur la loi de probabilité de l'écart maximum, Annales de la Société Polonaise de Mathematique, Cracovie Т. 6: 93–116.
- Johnson, Norman L.; Kotz, Samuel & Balakrishnan, N. (1994), Continuous univariate distributions. Vol. 1 (2nd ed.), Wiley Series in Probability and Mathematical Statistics: Applied Probability and Statistics, New York: John Wiley & Sons, ISBN 978-0-471-58495-7
- Muraleedharan, G.; Rao, A.D.; Kurup, P.G. & Nair, N. Unnikrishnan (2007), Modified Weibull Distribution for Maximum and Significant Wave Height Simulation and Prediction, Coastal Engineering Т. 54 (8): 630–638, DOI 10.1016/j.coastaleng.2007.05.001
- Muraleedharan, G. & Soares, C.G. (2014), Characteristic and Moment Generating Functions of Generalised Pareto (GP3) and Weibull Distributions, Journal of Scientific Research and Reports Т. 3 (14): 1861–1874, DOI 10.9734/JSRR/2014/10087.
- Rosin, P. & Rammler, E. (1933), The Laws Governing the Fineness of Powdered Coal, Journal of the Institute of Fuel Т. 7: 29–36.
- Sagias, Nikos C. & Karagiannidis, George K. (2005), Gaussian class multivariate Weibull distributions: theory and applications in fading channels, Institute of Electrical and Electronics Engineers. Transactions on Information Theory Т. 51 (10): 3608–3619, ISSN 0018-9448, doi:10.1109/TIT.2005.855598, <http://pelopas.uop.gr/~nsagias/Files/Papers/Journals/2005/J4_2005.pdf> (недоступная ссылка)
- Weibull, W. (1951), A statistical distribution function of wide applicability, J. Appl. Mech.-Trans. ASME Т. 18 (3): 293–297, <http://www.barringer1.com/wa_files/Weibull-ASME-Paper-1951.pdf>.
- Engineering statistics handbook. National Institute of Standards and Technology (2008).
- Nelson, Jr, Ralph Dispersing Powders in Liquids, Part 1, Chap 6: Particle Volume Distribution (5 февраля 2008). Дата обращения: 5 февраля 2008. Архивировано 13 февраля 2008 года.
- Левин Б.Р. Справочник по надежности. — Справочник по надежности/Под ред. Левина Б.Р., в 3 томах, Т.1. М.: Мир, 1969 г., 339 с.. — М.: Мир, 1969. — С. 176. — 339 с.
- J. Cheng, C. Tellambura, and N. C. Beaulieu Performance analysis of digital modulations on Weibull fading channels / Proc. IEEE Veh. Technol. Conf. 2004.
Ссылки
- Примеры графиков функции распределения Вейбулла (англ.)
- Распределение Вейбулла (англ.)
- Weibull Distribution (англ.)
- Построение графиков распределения Вейбулла в excel (рус.)
Для улучшения этой статьи по математике желательно: |
