Распределение Бернулли
| Распределение Бернулли | |
|---|---|
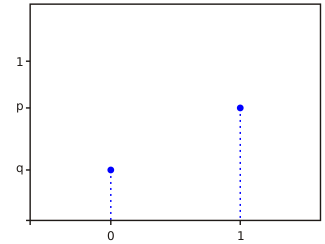 Функция вероятности Функция вероятности | |
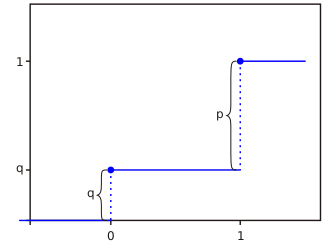 Функция распределения Функция распределения | |
| Параметры |
[math]\displaystyle{ p\in(0,1) }[/math] [math]\displaystyle{ q\equiv 1-p }[/math] |
| Носитель | [math]\displaystyle{ k=\{0,1\} }[/math] |
| Функция вероятности | [math]\displaystyle{ \begin{matrix} q & k=0 \\p~~ & k=1 \end{matrix} }[/math] |
| Функция распределения | [math]\displaystyle{ \begin{matrix} 0 & k\lt 0 \\q & 0\leq k\lt 1\\1 & k\geq 1 \end{matrix} }[/math] |
| Математическое ожидание | [math]\displaystyle{ p }[/math] |
| Мода | [math]\displaystyle{ \begin{cases} 0, & q \gt p\\ 0, 1, & q=p\\ 1, & q \lt p \end{cases} }[/math] |
| Дисперсия | [math]\displaystyle{ pq }[/math] |
| Коэффициент асимметрии | [math]\displaystyle{ \frac{q-p}{\sqrt{pq}} }[/math] |
| Коэффициент эксцесса | [math]\displaystyle{ \frac{6p^2-6p+1}{p(1-p)} }[/math] |
| Дифференциальная энтропия | [math]\displaystyle{ -q\ln q-p\ln p }[/math] |
| Производящая функция моментов | [math]\displaystyle{ q+pe^t }[/math] |
| Характеристическая функция | [math]\displaystyle{ q+pe^{it} }[/math] |
Распределе́ние Берну́лли в теории вероятностей и математической статистике — дискретное распределение вероятностей, моделирующее случайный эксперимент произвольной природы, при заранее известной вероятности успеха или неудачи.
Определение
Случайная величина [math]\displaystyle{ X }[/math] имеет распределение Бернулли, если она принимает всего два значения: [math]\displaystyle{ 1 }[/math] и [math]\displaystyle{ 0 }[/math] с вероятностями [math]\displaystyle{ p }[/math] и [math]\displaystyle{ q\equiv 1-p }[/math] соответственно. Таким образом:
- [math]\displaystyle{ \mathbb{P}(X=1) = p }[/math],
- [math]\displaystyle{ \mathbb{P}(X=0) = q }[/math].
Принято говорить, что событие [math]\displaystyle{ \{X=1\} }[/math] соответствует «успеху», а событие [math]\displaystyle{ \{X=0\} }[/math] — «неудаче». Эти названия условные, и в зависимости от конкретной задачи могут быть заменены на противоположные.
Свойства
Предельное свойство
Предельное свойство описывается теоремой Пуассона:
Пусть есть последовательность серий испытаний Бернулли, где [math]\displaystyle{ p_n }[/math] — вероятность «успеха», [math]\displaystyle{ \mu_n }[/math] — количество «успехов».
Тогда если
- [math]\displaystyle{ \lim_{n \to \infty} p_n = 0 ; }[/math]
- [math]\displaystyle{ \lim_{n \to \infty} n p_n = \lambda ; }[/math]
- [math]\displaystyle{ \lambda \gt 0, }[/math]
- то [math]\displaystyle{ \lim_{n \to \infty} P (\omega : \mu_n(\omega) = m) = e^{-\lambda} \cfrac {\lambda^m} {m!} . }[/math]
Моменты распределения Бернулли
- [math]\displaystyle{ \mathbb{E}[X] = p }[/math],
- [math]\displaystyle{ \operatorname{D}[X] = p(1-p)= pq }[/math], так как: [math]\displaystyle{ \operatorname{E}X^2-\left(\operatorname{E}X\right)^2=p-p^2 = p\cdot(1-p) = pq }[/math].
Вообще, легко видеть, что
- [math]\displaystyle{ \mathbb{E}\left[X^n\right] = \Pr(X=1)\cdot 1^n + \Pr(X=0)\cdot 0^n = p \cdot 1^n + q\cdot 0^n = p = \mathbb{E}[X], \forall n \in \mathbb{N} }[/math]
Замечание
Если независимые случайные величины [math]\displaystyle{ X_1,\ldots ,X_n }[/math], имеют распределение Бернулли с вероятностью успеха [math]\displaystyle{ p }[/math], то
- [math]\displaystyle{ Y = \sum\limits_{i=1}^nX_i }[/math]
имеет биномиальное распределение с [math]\displaystyle{ n }[/math] степенями свободы.
См. также
Литература
- Hazewinkel, Michiel, ed. (2001), "Binomial distribution", Encyclopedia of Mathematics, Springer, ISBN 978-1-55608-010-4
Для улучшения этой статьи по математике желательно: |