Преобразование геодезических систем координат

Эта статья находится на начальном уровне проработки, в одной из её версий выборочно используется текст из источника, распространяемого под свободной лицензией
Материал из энциклопедии Руниверсалис

В геодезии задача перехода между различными системами координат возникает из-за существования множества систем координат, возникающих во всем мире на протяжении долгого времени. Применение различных систем координат при решении практических задач геодезии, картографии, навигации и в геоинформационных системах неизбежно. Различают несколько типов преобразования координат: переход между различными форматами координат, переход между различными системами координат и картографическими проекциями, а также преобразование датумов. Все перечисленные виды преобразования будут рассмотрены в данной статье.[1]

Изменение формата и единиц

Обозначить географическое место обычно значит передать широту и долготу места. Числовые значения для широты и долготы могут быть представлены в нескольких различных видах единиц и форматах:[2]

шестидесятеричная система: градусы, минуты и секунды: 40° 26′ 46″ N 79° 58′ 56″ W

градусы и десятичные минуты: 40° 26.767′ N 79° 58.933′ W

десятичные градусы: 40,446° N 79,982° W

В градусе 60 минут, а в минуте 60 секунд. Поэтому для перевода из формата градусы/минуты/секунды в формат десятичных градусов можно использовать формулу:

десятичные градусы=градусы+минуты/60+секунды/3600.

Для обратного перевода из формата десятичных градусов в формат градусы/минуты/секунды можно использовать формулы:

градусы=[десятичные градусы]

минуты=[60*(десятичные градусы-градусы)]

секунды=3600*(десятичные градусы-градусы)-60*минуты

где обозначение [x] значит, что надо взять целую часть x, и обратиться к «полочной функции».

Переход между различными системами координат

Преобразование системы координат — это переход из одной системы координат в другую, причём обе системы координат основаны на одном и том же геодезическом датуме. Часто задача преобразования заключается в переходе от геодезической системы координат к прямоугольным координатам либо переход от одной картографической проекции к другой.

Из геодезической системы координат в прямоугольную

Прямоугольные координаты точек в пространстве можно вычислить по известным геодезическим координатам этих точек (широта B, долгота L, высота H) по формулам:[3]

[math]\displaystyle{ \begin{align} X & = \left( N(B) + H\right)\cos{B}\cos{L} \\ Y & = \left( N(B) + H\right)\cos{B}\sin{L} \\ Z & = \left( \frac{b^2}{a^2} N(B) + H\right)\sin{B} \end{align} }[/math]

где

[math]\displaystyle{ N(B) = \frac{a^2}{\sqrt{a^2 \cos^2 B + b^2 \sin^2 B }} = \frac{a}{\sqrt{1-e^2\sin^2B}}, }[/math]

где [math]\displaystyle{ a }[/math] и [math]\displaystyle{ b }[/math] — экваториальный (большая полуось) и полярный радиусы (малая полуось), соответственно. [math]\displaystyle{ e^2 =\frac{a^2-b^2}{a^2} }[/math] — квадрат первого эксцентриситета эллипсоида. [math]\displaystyle{ \, N(B) }[/math] радиус кривизны первого вертикала — расстояние по нормали к эллипсоиду от точки пересечения поверхности эллипсоида нормалью до оси oZ (Рис. 1).

Из прямоугольной системы координат в геодезическую

При переходе от прямоугольных пространственных координат к геодезической системе координат (такой как WGS84) геодезические широты B и высоты H зачастую требуется вычислять итеративными методами, то есть выполнением последовательных приближений. Что касается долгот L, то они вычисляются обычным путём.

Существует несколько методов для вычислений геодезических широт и высот, рассмотрим два из них.

Метод Ньютона-Рафсона

Следующее иррациональное уравнение Боуринга[4] для геодезической широты решается итерационным методом Ньютона — Рафсона:[5][6]

[math]\displaystyle{ \kappa - 1 - \frac{e^2 a \kappa}{\sqrt{p^2+(1-e^2) Z^2 \kappa^2 }} = 0, }[/math]

где [math]\displaystyle{ p=\sqrt{x^2+y^2} }[/math],

Широту B можно найти из уравнения [math]\displaystyle{ \kappa = \frac{p}{Z} \tan(B) }[/math].

Высота H рассчитывается как:

[math]\displaystyle{ H= e^{-2} (\kappa^{-1} - {\kappa_0}^{-1}) \sqrt{p^2+ Z^2 \kappa^2 }. }[/math]

Итерация может быть преобразована к следующему виду:

[math]\displaystyle{ \kappa_{i+1} = \frac{c_i+\left(1- e^2\right) Z^2 \kappa_i ^3 }{c_i- p^2} = 1 + \frac{p^2+\left(1- e^2\right) Z^2 \kappa_i ^3 }{c_i- p^2} , }[/math]

где [math]\displaystyle{ c_i = \frac{\left(p^2+\left(1-e^2\right) Z^2 \kappa_i ^2\right)^{3/2}}{a e^2} , }[/math] [math]\displaystyle{ \kappa_0= \left( 1-e^2 \right)^{-1} . }[/math]

Постоянная [math]\displaystyle{ \, \kappa_0 }[/math] является хорошим начальным значением для итерации, когда [math]\displaystyle{ H\approx0 }[/math]. Боуринг показал, что в таком случаи уже первая итерация дает достаточно точное решение. Он использовал дополнительные тригонометрические функции в своей первоначальной формулировке.

Решение Ferrari

Вышеизложенное уравнение для [math]\displaystyle{ \kappa }[/math] можно решить методом Феррари:[7][8]

[math]\displaystyle{ \begin{align} \zeta &= (1 - e^2) z^2 / a^2 ,\\[6pt] \rho &= (p^2 / a^2 + \zeta - e^4) / 6 ,\\[6pt] s &= e^4 \zeta p^2 / ( 4 \rho^3 a^2) ,\\[6pt] t &= \sqrt[3]{1 + s + \sqrt{s (s + 2)}} ,\\[6pt] u &= \rho (1 + t + 1 / t) ,\\[6pt] v &= \sqrt{u^2 + e^4 \zeta} ,\\[6pt] w &= e^2 (u + v - \zeta) / (2 v) ,\\[6pt] \kappa &= 1 + e^2 (\sqrt{u + v + w^2} + w) / (u + v). \end{align} }[/math]

Применение решения Феррари

Существует ряд методов и алгоритмов, но наиболее точным, согласно Чжу[9], является следующая последовательность, установленная Хейккиненом[10]. Предполагается, что геодезические параметры известны.

[math]\displaystyle{ \begin{matrix} r &=& \sqrt{X^2+Y^2}\\ e'^2 &=& (a^2 - b^2) / b^2\\ F &=& 54b^2Z^2\\ G &=& r^2 + (1-e^2)Z^2 - e^2(a^2 - b^2)\\ c &=& \frac{e^4Fr^2}{G^3}\\ s &=& \sqrt[3]{1+c+\sqrt{c^2 + 2c}}\\ P &=& \frac{F}{3\left(s+\frac{1}{s}+1\right)^2G^2}\\ Q &=& \sqrt{1+2e^4P}\\ r_0 & =& \frac{-(Pe^2r)}{1+Q} + \sqrt{\frac12 a^2\left(1+1/Q\right) - \frac{P(1-e^2)Z^2}{Q(1+Q)} - \frac12 Pr^2}\\ U &=& \sqrt{(r - e^2r_0)^2 + Z^2} \\ V &=& \sqrt{(r-e^2r_0)^2 + (1-e^2)Z^2}\\ z_0 &=& \frac{b^2Z}{aV}\\ H &=& U\left(1-\frac{b^2}{aV}\right)\\ B & = & \arctan\left[ \frac{Z+e'^2z_0}{r}\right] \\ L &=& \arctan2[Y,X] \end{matrix} }[/math]

Примечание: arctan2 [Y, X] — обратная касательная к четырем квадрантам.

Степенной ряд

Для малых е2 степенной ряд [math]\displaystyle{ \kappa = \sum_{i\ge 0} \alpha_i e^{2i} }[/math] начинается с

[math]\displaystyle{ \alpha_0 = 1; }[/math]
[math]\displaystyle{ \alpha_1=\frac{a}{\sqrt{Z^2+p^2}}; }[/math]
[math]\displaystyle{ \alpha_2=\frac{aZ^2\sqrt{Z^2+p^2}+2a^2p^2}{2(Z^2+p^2)^2}. }[/math]

Переход из геодезической системы координат в ENU и обратно

Преобразование из геодезических координат в топоцентрические координаты ENU состоит их двух этапов:

  1. Преобразование координат из геодезической системы в прямоугольную.
  2. Преобразование координат из прямоугольной в топоцентрическую систему координат ENU.

Преобразование координат из прямоугольной в топоцентрическую систему координат ENU

Чтобы преобразовать прямоугольные координаты в топоцентрические необходимо знать начальную точку топоцентрической системы координат, обычно она располагается в некоторой точке наблюдений. Если наблюдение производится в точке [math]\displaystyle{ \{X_r, Y_r, Z_r\} }[/math] , а наблюдаемый объект в [math]\displaystyle{ \{X_p, Y_p, Z_p\} }[/math] тогда радиус-вектор этого направления в системе координат ENU имеет вид:

[math]\displaystyle{ \begin{bmatrix} x \\ y \\ z\\ \end{bmatrix} = \begin{bmatrix} -\sin L_r & \cos L_r & 0 \\ -\sin B_r\cos L_r & -\sin B_r\sin L_r & \cos B_r \\ \cos B_r\cos L_r & \cos B_r\sin L_r& \sin B_r \end{bmatrix} \begin{bmatrix} X_p - X_r \\ Y_p-Y_r \\ Z_p - Z_r \end{bmatrix} }[/math]

Преобразование координат из топоцентрической системы координат ENU в прямоугольную.

Путём обратного преобразования координат из прямоугольной системы получим топоцентрическую систему координат:

[math]\displaystyle{ \begin{bmatrix} X\\ Y\\ Z\\ \end{bmatrix} = \begin{bmatrix} -\sin\lambda & -\sin\phi\cos\lambda &\cos\phi\cos\lambda \\ \cos\lambda & -\sin\phi\sin\lambda & \cos\phi\sin\lambda \\ 0 & \cos\phi& \sin\phi \end{bmatrix} \begin{bmatrix} x \\ y \\ z \end{bmatrix} + \begin{bmatrix} X_r \\ Y_r \\ Z_r \end{bmatrix} }[/math]

Переход к другой картографической проекции

Преобразование координат и положений на карте между различными картографическими проекциями карты, привязанные к одной и тоже геодезической поверхности, может быть выполнено либо с помощью формул прямого перехода из одной проекции в другую, либо сначала проекция [math]\displaystyle{ A }[/math] преобразуется в промежуточную систему координат, такую ​​как прямоугольная, а уже из неё в проекцию [math]\displaystyle{ B }[/math]. Используемые формулы могут быть сложными, в некоторых случаях преобразование не имеет решения в замкнутой форме, и необходимо использовать приближенные методы. Обычно для выполнения задач преобразования координат используются компьютерные программы, например, с программой GEOTRANS, поддерживаемой DoD и NGA.[11]

Преобразования датумов

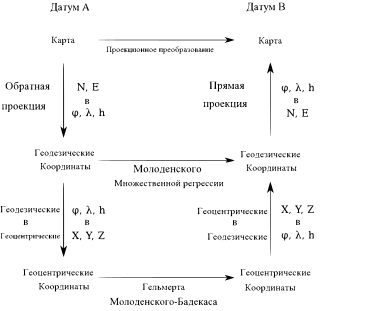
Переход-между-основами.svg

Преобразования между датумами могут быть выполнены различными способами. Существуют преобразования, которые позволяют совершить прямой переход от геодезических координат одного датума к геодезическим координатам другого датума. Существуют менее прямые переходы, которые преобразуют геодезические координаты в геоцентрические (ECEF), преобразуют геоцентрические координаты из одного датума в другой, затем преобразуют геоцентрические координаты другого датума обратно в геодезические. Также существуют проекционные преобразования, которые позволяют совершить прямой переход из одной (датум, проекция) пары к другой (датум, проекция) паре.

Проекционные преобразования

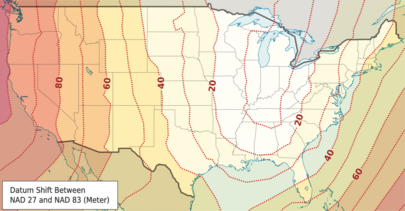
Базовое смещение между NAD27 и NAD83 — На карте показана приблизительная величина (в метрах) общего сдвига между одним и тем же набором значений координат на север и восток в NAD27 и NAD83

Проекционные преобразования позволяют совершить прямой переход от координат на карте для одной (картографическая проекция, датум) пары к координатам на карте для другой (картографическая проекция, датум) пары. Как пример можно привести метод NADCON для преобразования от Северо — Американского датума (North American Datum) (NAD) 1927 года к датуму NAD[en] 1983 года[12]. Высокоточная эталонная сеть (The High Accuracy Reference Network) (HARN), высокоточная версия преобразований NADCON, имеет точность приблизительно 5 сантиметров. Национальное преобразование версия 2(The National Transformation version 2) (NTv2) является канадской версией NADCON для перехода между NAD 1927 и NAD 1983[en]. Методы HARN также известны, как NAD 83/91 и Высокоточные проекционные сети (High Precision Grid Networks) (HPGN)[13]. Впоследствии, Австралия и Новая Зеландия адаптировали для себя формат NTv2 для того, чтобы создать методы проекционных преобразований для переходов между их собственными местными датумами.

Как и преобразования с помощью уравнений множественной регрессии, проекционные методы используют интерполяцию низких порядков для преобразования координат карты, но в двух пространствах вместо трех. NOAA предоставляет программное обеспечение (как часть NGS Geodetic Toolkit) для производства преобразований NADCON.[14][15]

Преобразование Молоденского

Преобразование Молоденского позволяет совершить прямой переход между геодезическими координатами разных датумов без необходимости промежуточного перехода к геоцентрическим координатам.[16] Для него требуются три смещения между центрами систем координат и разницы между большими полуосями и параметрами сжатия референц-эллипсоидов.

Преобразование Молоденского используется Национальным агентством геопространственной разведки (National Geospatial-Intelligence Agency) (NGA) в их техническом сообщении TR8350.2, а также в программе GEOTRANS, поддерживаемой агентством.[17] Преобразование Молоденского было популярно до прихода эры современных компьютеров, и метод является частью многих геодезических программ.

Уравнения множественной регрессии

Преобразования датумов с использованием эмпирических методов множественной регрессии были созданы для достижения большей точности для маленьких географических регионов чем стандартные преобразования Молоденского. Данные преобразования используются для преобразования местных датумов, которые создаются для континентов или меньших регионов, в глобальные датумы, такие как WGS 84.[18] В стандарте NIMA TM 8350.2, Приложение D[19] перечислены преобразования с помощью уравнений множественной регрессии от нескольких местных датумов к WGS 84, с точностью около 2 метров.[20]

Метод уравнений множественной регрессии позволяет совершить прямое преобразование геодезических координат без промежуточного перевода в геоцентрические координаты. Геодезические координаты [math]\displaystyle{ \phi_B, \lambda_B, h_B }[/math] в новом датуме B моделируются как полиномы вплоть до девятой степени в геодезических координатах [math]\displaystyle{ \phi_A, \lambda_A, h_A }[/math]изначального датума A. Например, приращение [math]\displaystyle{ \phi_B }[/math]может быть разложено как (показано разложение только до квадратичных членов):

[math]\displaystyle{ \Delta \phi = a_0 + a_1 U + a_2 V + a_3 U^2 + a_4 UV + a_5 V^2 + \cdots }[/math]

где

[math]\displaystyle{ \begin{align} a_i & = \mbox {параметры подобранные множественной регрессией} \\ U & = K(\phi_A - \phi_m) \\ V & = K(\lambda_A - \lambda_m) \\ K & = \mbox {фактор масштаба} \\ \phi_m,\lambda_m & = \mbox {начало датума }A \\ \end{align} }[/math]

для [math]\displaystyle{ \Delta\lambda }[/math] и [math]\displaystyle{ \Delta h }[/math] выстраиваются схожие уравнения. При достаточном количестве пар координат (A, B) для точек в обоих датумах для хорошей статистики используются множественные методы регрессии для подбора параметров этих полиномов. Полиномы, вместе с подобранными коэффициентами, формируют уравнения множественной регрессии.

Преобразование Гельмерта

Использование преобразования Гельмерта[en] при переходе от геодезических координат датума [math]\displaystyle{ A }[/math] к геодезическим координатам датума [math]\displaystyle{ B }[/math] происходит в три шага:

1 Преобразование геодезических координат датума [math]\displaystyle{ A }[/math] в геоцентрические;

2 Применение преобразования Гельмерта, с соответствующими параметрами преобразования для [math]\displaystyle{ A\to B }[/math], для перехода от геоцентрических координат датума [math]\displaystyle{ A }[/math] к геоцентрическим координатам датума [math]\displaystyle{ B }[/math];

3 Преобразование геоцентрических координат в геодезические координаты для датума [math]\displaystyle{ B }[/math].

Для геоцентрических координат XYZ преобразование Гельмерта[en] имеет форму:[21]

[math]\displaystyle{ \begin{bmatrix} X_B \\ Y_B \\ Z_B \end{bmatrix} = \begin{bmatrix} c_x \\ c_y \\ c_z \end{bmatrix} + (1 + s\times10^{-6}) \cdot \begin{bmatrix} 1&-r_z&r_y \\ r_z&1&-r_x \\ -r_y & r_x & 1 \end{bmatrix} \cdot \begin{bmatrix} X_A \\ Y_A \\ Z_A \end{bmatrix}. }[/math]

Преобразование Гельмерта это преобразование с семью элементами, с тремя параметрами смещения [math]\displaystyle{ c_x, c_y, c_z }[/math], тремя параметрами разворота [math]\displaystyle{ r_x, r_y, r_z }[/math] и одним масштабным параметром [math]\displaystyle{ s }[/math]. Преобразование Гельмерта это приближенный метод, который можно считать точным только, когда параметры преобразования малы по сравнению с величинами векторов геоцентрической системы координат. С такими условиями преобразование можно считать обратимым.[22]

Преобразование Гельмерта с четырнадцатью параметрами, с линейной зависимостью от времени для каждого параметра, может быть использовано для наблюдений за изменением во времени географических координат из-за геоморфологических процессов, таких как континентальный дрейф[23] и землетрясения.[24] Оно было преобразовано в программное обеспечение, такое как инструмент Horizontal Time Dependent Positioning (HTDP) в программном обеспечении U.S. NGS.[25]

Преобразование Молоденского — Бадекаса

Для исключения связи между смещениями и разворотами преобразования Гельмерта могут быть использованы три дополнительных параметра, чтобы получить новый XYZ центр разворота ближе к преобразуемым координатам. Это преобразование с десятью параметрами называется преобразованием Молоденского — Бадекаса, его не стоит путать с более простым преобразованием Молоденского.

Как при использовании преобразования Гельмерта, использование преобразования Молоденского — Бадекаса состоит из трех шагов:

  1. Преобразование геодезических координат датума [math]\displaystyle{ A }[/math] в геоцентрические.
  2. Применение преобразования Молоденского — Бадекаса, с соответствующими параметрами преобразования для [math]\displaystyle{ A\to B }[/math], для перехода от геоцентрических координат датума [math]\displaystyle{ A }[/math] к геоцентрическим координатам датума [math]\displaystyle{ B }[/math].
  3. Преобразование геоцентрических координат в геодезические координаты для датума [math]\displaystyle{ B }[/math].

Преобразование имеет форму[26]:

[math]\displaystyle{ \begin{bmatrix} X_B \\ Y_B \\ Z_B \end{bmatrix} = \begin{bmatrix} X_A \\ Y_A \\ Z_A \end{bmatrix} + \begin{bmatrix} \Delta X_A \\ \Delta Y_A \\ \Delta Z_A \end{bmatrix} + \begin{bmatrix} 1&-r_z&r_y \\ r_z&1&-r_x \\ -r_y & r_x & 1 \end{bmatrix} \cdot \begin{bmatrix} X_A-X^0_A \\ Y_A-Y^0_A \\ Z_A-Z^0_A \end{bmatrix} + \Delta S \begin{bmatrix} X_A-X^0_A \\ Y_A-Y^0_A \\ Z_A-Z^0_A \end{bmatrix}. }[/math]
где [math]\displaystyle{ (X^0_A,~Y^0_A,~Z^0_A) }[/math] — начало отсчёта для разворота и масштабного преобразования, а [math]\displaystyle{ \Delta S }[/math] — масштабный фактор.

Преобразование Молоденского — Бадекаса используется для преобразования местных геодезических датумов в глобальные датумы, такие как WGS 84. В отличие от преобразования Гельмерта, преобразование Молоденского — Бадекаса необратимо из-за того, что начало отсчёта для разворота относится к изначальному датуму.

См. также

Ссылки на литературу

  1. ↑ Roger Foster Dan Mullaney Basic Geodesy Article 018: Conversions and Transformations (4 марта 2014). Дата обращения: 9 декабря 2019. Архивировано 27 ноября 2020 года.
  2. ↑ Ordnance Survey Great Britain. Coordinate transformer. Дата обращения: 9 декабря 2019. Архивировано 12 августа 2013 года.
  3. ↑ B. Hofmann-Wellenhof H. Lichtenegger J. Collins. GPS - theory and practice. — 282 с. — ISBN 3-211-82839-7.
  4. ↑ Bowring B. R. Transformation from Spatial to Geographical Coordinates // Surv. Rev.. — 1976. — Т. 23, № 181. — С. 323—327. — doi:10.1179/003962676791280626.
  5. ↑ Fukushima, T. Fast Transform from Geocentric to Geodetic Coordinates (англ.) // J. Geod. : journal. — 1999. — Vol. 73, no. 11. — P. 603—610. — doi:10.1007/s001900050271. (Appendix B)
  6. ↑ Sudano, J. J. (1997). «An exact conversion from an earth-centered coordinate system to latitude, longitude and altitude». doi:10.1109/NAECON.1997.622711
  7. ↑ Direct Transformation from Geocentric to Geodetic Coordinates // Vermeille, H.H J. Geod.. — 2002. — Т. 76. — С. 451—454. — doi:10.1007/s00190-002-0273-6.
  8. ↑ Irene PoloBlanco Gonzalez-Vega. A symbolic analysis of Vermeille and Borkowski polynomials for transforming 3D Cartesian to geodetic coordinates // J. Geod.. — 2009. — Т. 83. — С. 1071—1081. — doi:10.1007/s00190-009-0325-2.
  9. ↑ J.Zhu. Conversion of Earth-centered Earth-fixed coordinates to geodetic coordinates // IEEE Transactions on Aerospace and Electronic Systems. — 1994. — Т. 30. — С. 957—961. — doi:10.1109/7.303772.
  10. ↑ M.Heikkinen. Geschlossene formeln zur berechnung räumlicher geodätischer koordinaten aus rechtwinkligen koordinaten // Z. Vermess.. — 1982. — Т. 107. — С. 207—211.
  11. ↑ MSP GEOTRANS 3.3 (Geographic Translator) (недоступная ссылка). NGA: Coordinate Systems Analysis Branch. Дата обращения: 9 декабря 2019. Архивировано 15 марта 2014 года.
  12. ↑ ArcGIS Help 10.1: Grid-based methods. ESRI. Дата обращения: 9 декабря 2019. Архивировано 4 декабря 2019 года.
  13. ↑ NADCON/HARN Datum ShiftMethod. bluemarblegeo.com. Дата обращения: 9 декабря 2019. Архивировано 6 марта 2014 года.
  14. ↑ NADCON - Version 4.2. NOAA. Дата обращения: 9 декабря 2019. Архивировано 6 мая 2021 года.
  15. ↑ Donald M. Mulcare. NGS Toolkit, Part 8: The National Geodetic Survey NADCON Tool (недоступная ссылка). Professional Surveyor Magazine. Архивировано 6 марта 2014 года.
  16. ↑ ArcGIS Help 10.1: Equation-based methods. ESRI. Дата обращения: 9 декабря 2019. Архивировано 4 декабря 2019 года.
  17. ↑ Datum Transformations. National Geospatial-Intelligence Agency. Дата обращения: 9 декабря 2019. Архивировано 9 октября 2014 года.
  18. ↑ User's Handbook on Datum Transformations Involving WGS 84. — 3rd. — Monaco : International Hydrographic Bureau, August 2008.
  19. ↑ DEPARTMENT OF DEFENSE WORLD GEODETIC SYSTEM 1984 Its Definition and Relationships with Local Geodetic Systems. National Imagery and Mapping Agency (NIMA). Дата обращения: 9 декабря 2019. Архивировано 11 апреля 2014 года.
  20. ↑ Taylor Chuck. High-Accuracy Datum Transformations. Дата обращения: 9 декабря 2019. Архивировано 4 января 2013 года.
  21. ↑ Equations Used for Datum Transformations. Land Information New Zealand (LINZ). Дата обращения: 9 декабря 2019. Архивировано 6 марта 2014 года.
  22. ↑ Geomatics Guidance Note Number 7, part 2 Coordinate Conversions and Transformations including Formulas (недоступная ссылка). International Association of Oil and Gas Producers (OGP). Архивировано 6 марта 2014 года.
  23. ↑ Paul Bolstad. GIS Fundamentals, 4th Edition. — Atlas books. — 93 с. — ISBN 978-0-9717647-3-6.
  24. ↑ Addendum to NIMA TR 8350.2: Implementation of the World Geodetic System 1984 (WGS 84) Reference Frame G1150. National Geospatial-Intelligence Agency. Дата обращения: 9 декабря 2019. Архивировано 11 мая 2012 года.
  25. ↑ HTDP - Horizontal Time-Dependent Positioning. U.S. National Geodetic Survey (NGS). Дата обращения: 9 декабря 2019. Архивировано 25 ноября 2019 года.
  26. ↑ Molodensky-Badekas (7+3) Transformations. National Geospatial Intelligence Agency (NGA). Дата обращения: 9 декабря 2019. Архивировано 19 июля 2013 года.

Примечания

Источник — https://xn--h1ajim.xn--p1ai/index.php?title=Преобразование_геодезических_систем_координат&oldid=12605929