Момент силы
| Момент силы | |
|---|---|
| [math]\displaystyle{ \vec{M}=\left[\vec{r}\times\vec{F}\right] }[/math] | |
| Размерность | L2MT−2 |
| Единицы измерения | |
| СИ | Н·м |
| СГС | Дина-сантиметр |
| Примечания | |
| Псевдовектор | |
Моме́нт си́лы (момент силы относительно точки) — векторная физическая величина, характеризующая действие силы на механический объект, которое может вызвать его вращательное движение. Определяется как векторное произведение радиус-вектора точки приложения силы [math]\displaystyle{ \vec{r} }[/math] и вектора силы [math]\displaystyle{ \vec{F} }[/math]. Моменты сил, образующиеся в разных условиях, в технике могут иметь названия: кру́тящий момент, враща́тельный момент, вертя́щий момент, враща́ющий момент, скру́чивающий момент.
Момент силы обозначается символом [math]\displaystyle{ \vec{M} }[/math] или, реже, [math]\displaystyle{ \vec{\tau} }[/math] (тау).
Единица измерения в СИ: Н⋅м. Величина момента силы зависит от выбора начала отсчёта радиус-векторов O.
Понятие момента силы используется, в основном, в области задач статики и задач, связанных с вращением деталей (рычагов и др.) в технической механике. Особенно важен случай вращения твёрдого тела вокруг фиксированной оси — тогда O выбирают на этой оси, а вместо самого момента рассматривают его проекцию на ось [math]\displaystyle{ M_{\parallel} }[/math]; такая проекция называется моментом силы относительно оси.
Наличие момента силы влечёт изменение момента импульса тела [math]\displaystyle{ \vec{L} }[/math] относительно того же начала O со временем [math]\displaystyle{ t }[/math]: имеет место соотношение [math]\displaystyle{ d\vec{L}/dt = \vec{M} }[/math]. В статике равенство нулю суммы моментов всех приложенных к телу сил является одним из условий (наряду с равенством нулю суммы сил) реализации состояния покоя.
Определение, общие сведения
В физике момент силы играет роль вращающего воздействия на тело.
В простейшем случае, если сила [math]\displaystyle{ \vec{F} }[/math] приложена к рычагу перпендикулярно ему и оси вращения, то момент силы определяется как произведение величины [math]\displaystyle{ F }[/math] на расстояние [math]\displaystyle{ x }[/math] от места приложения силы до оси вращения рычага, называемое «плечом силы»:
- [math]\displaystyle{ M = [{\rm force}] \cdot [{\rm force\,arm}] = Fx }[/math].
Например, сила в 3 ньютона, приложенная на расстоянии 2 м от оси, создаёт такой же момент, что и сила в 1 ньютон с плечом 6 м.
Если действуют две силы, говорят о моменте пары сил (такая формулировка восходит к трудам Архимеда). При этом равновесие достигается в ситуации [math]\displaystyle{ F_1x_1 = F_2x_2 }[/math].
Для случаев более сложных движений и более сложных объектов определение момента как произведения [math]\displaystyle{ Fx }[/math] требует универсализации.
Момент силы иногда называют вращающим или крутящим моментом. «Вращающий» момент понимается в технике как внешнее усилие, прикладываемое к объекту, а «крутящий» — как внутреннее, возникающее в самом объекте под действием приложенных нагрузок (этим понятием оперируют в сопромате).
Момент силы относительно точки
В общем случае момент силы [math]\displaystyle{ \vec{F} }[/math], приложенной к телу, определяется как векторное произведение
- [math]\displaystyle{ \vec M = \left[\vec r\times\vec F\right] }[/math],
где [math]\displaystyle{ \vec{r} }[/math] — радиус-вектор точки приложения силы. Вектор [math]\displaystyle{ \vec{M} }[/math] перпендикулярен векторам [math]\displaystyle{ \vec{r} }[/math] и [math]\displaystyle{ \vec{F} }[/math].
Начало отсчета радиус-векторов O может быть любым. Обычно O выбирают в чем-либо выделенной точке: в месте закрепления подвеса, в центре масс, на оси вращения и т.д.. Если одновременно анализируется момент импульса тела [math]\displaystyle{ \vec{L} }[/math], то начало O всегда выбирается одинаковым для [math]\displaystyle{ \vec{L} }[/math] и [math]\displaystyle{ \vec{M} }[/math].
Если не оговорено иное, то «момент силы» — это момент силы относительно точки (O), а не некоей оси.
В случае нескольких приложенных сосредоточенных сил их моменты векторно суммируются:
- [math]\displaystyle{ \vec M = \sum_i\left[\vec{r}_i\times\vec{F}_i\right] }[/math],
где [math]\displaystyle{ \vec{r}_i }[/math] — радиус-вектор точки приложения [math]\displaystyle{ i }[/math]-й силы [math]\displaystyle{ \vec{F}_i }[/math]. В случае силы, распределённой с плотностью [math]\displaystyle{ d\vec{F}/dV }[/math],
- [math]\displaystyle{ \vec M = \int\limits_V\left[\vec{r}\times\frac{d\vec{F}}{dV}\right]dV }[/math].
Если [math]\displaystyle{ d\vec{F}/dV }[/math] (Н/м3) — обобщённая функция, которая может содержать и дельтаобразные члены, то последней формулой охватываются и две предыдущие.
Момент силы относительно оси
Моментом силы относительно оси называется алгебраическое значение проекции момента [math]\displaystyle{ \vec{M} }[/math] на ось, то есть
- [math]\displaystyle{ M_{\parallel} = \vec{M}\cdot \vec{e}_o }[/math],
где [math]\displaystyle{ \vec{e}_o }[/math] — единичный вектор вдоль оси, а начало отсчёта O выбрано на оси. Момент силы относительно оси может быть рассчитан как
- [math]\displaystyle{ M_{\parallel} = \pm\left|\vec{r}_{\perp}\times\vec{F}_{\perp}\right| }[/math],
где через [math]\displaystyle{ \vec{r}_{\perp} }[/math] и [math]\displaystyle{ \vec{F}_{\perp} }[/math] обозначены составляющие радиус-вектора и силы в плоскости, перпендикулярной оси.
В отличие от момента силы [math]\displaystyle{ \vec{M} }[/math], величина момента силы относительно оси [math]\displaystyle{ M_{\parallel} }[/math] не претерпевает изменения при сдвиге точки O вдоль оси.
Для краткости символ параллельности и знак могут опускаться, а [math]\displaystyle{ M_{\parallel} }[/math] (как и [math]\displaystyle{ \vec{M} }[/math]) именоваться «моментом силы».
Единицы измерения
Момент силы имеет размерность «сила, умноженная на расстояние» и единицу измерения ньютон-метр в системе СИ. 1 Н·м — это момент, который производит сила 1 Н на рычаг длиной 1 м, приложенная к концу рычага и направленная перпендикулярно ему.
Формально, размерность [math]\displaystyle{ \vec{M} }[/math] (Н·м) совпадает с размерностями энергии и механической работы. Но использование единицы «джоуль» в данном контексте нежелательно, так как этим затушёвывается физический смысл.
Некоторые примеры
Формула момента рычага
Момент силы, действующей на рычаг, равен
- [math]\displaystyle{ \vec{M} = r F \sin\alpha\cdot\vec{e}_o }[/math]
или, если записать момент силы относительно оси,
- [math]\displaystyle{ M_{\parallel} = r F\sin\alpha }[/math],
где [math]\displaystyle{ \alpha }[/math] — угол между направлением силы и рычагом. Плечо силы равно [math]\displaystyle{ r\sin\alpha }[/math]. Максимальное значение момента достигается при перпендикулярности рычага и силы, то есть при [math]\displaystyle{ \alpha = \pi/2 }[/math]. При сонаправленности [math]\displaystyle{ \vec{F} }[/math] и рычага момент равен нулю.
Статическое равновесие
Для того чтобы объект находился в равновесии, должна равняться нулю не только сумма всех сил, но и сумма моментов всех сил вокруг любой точки.
Для двумерного случая с горизонтальными и вертикальными силами требование сводится к тому, чтобы нулевыми были сумма сил в двух измерениях: [math]\displaystyle{ \Sigma F_{horizontal}=0,\, \Sigma F_{vertical}=0 }[/math] и момент силы в третьем измерении: [math]\displaystyle{ \Sigma M=0 }[/math].
Движение твёрдого тела
Движение твёрдого тела можно представить как движение конкретной точки и вращения вокруг неё.
Момент импульса относительно точки O твёрдого тела может быть описан через произведение момента инерции и угловой скорости относительно центра масс и линейного движения центра масс.
- [math]\displaystyle{ \vec{L_o} = I_c\,\vec\omega + [M(\vec{r_o} - \vec{r_c}), \vec{v_c}]. }[/math]
Будем рассматривать вращающиеся движения в системе координат Кёнига, так как описывать движение твёрдого тела в мировой системе координат гораздо сложнее.
Продифференцируем это выражение по времени. И если [math]\displaystyle{ I }[/math] — постоянная величина во времени, то
- [math]\displaystyle{ \vec M = I\frac{d\vec\omega}{dt} = I\vec\alpha, }[/math]
где [math]\displaystyle{ \vec\alpha }[/math] — угловое ускорение, измеряемое в радианах в секунду за секунду (рад/с2). Пример: вращается однородный диск.
Если тензор инерции меняется со временем, то движение относительно центра масс описывается с помощью динамического уравнения Эйлера:
- [math]\displaystyle{ \vec{M_c} = I_c\frac{d\vec\omega}{dt} + [\vec w, I_c\vec w]. }[/math]
Связь с другими величинами
С моментом импульса
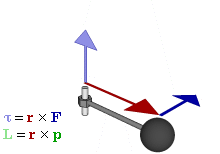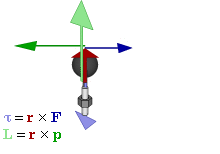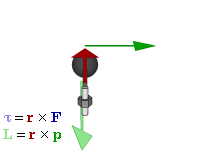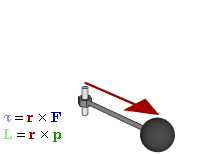
Момент силы — производная момента импульса [math]\displaystyle{ \vec L = \vec{r}\times\vec{p} }[/math] относительно точки O по времени:
- [math]\displaystyle{ \vec M = \frac{d\vec L}{dt} }[/math],
Аналогичную формулу можно записать для моментов относительно оси:
- [math]\displaystyle{ M_{\parallel} = \frac{dL_{\parallel}}{dt} }[/math].
Если момент силы [math]\displaystyle{ \vec{M} }[/math] или [math]\displaystyle{ M_{\parallel} }[/math] равен нулю, момент импульса относительно соответствующей точки или оси сохраняется.
С мощностью
Если сила совершает действие на каком-либо расстоянии, то она совершает механическую работу и развивает мощность [math]\displaystyle{ \vec{F}\cdot\vec{v} }[/math] (где [math]\displaystyle{ \vec{v} }[/math] — скорость материальной точки). Так же и в случае момента силы: если он совершает действие через «угловое расстояние», развивается мощность
- [math]\displaystyle{ P = \vec M \cdot \vec\omega }[/math].
В системе СИ мощность [math]\displaystyle{ P }[/math] измеряется в ваттах, угловая скорость [math]\displaystyle{ \vec{\omega} }[/math] — в радианах в секунду.
С механической работой
Если под действием момента силы [math]\displaystyle{ \vec{M} }[/math] происходит поворот тела на угол [math]\displaystyle{ d\varphi }[/math], то совершается механическая работа
- [math]\displaystyle{ dA = \left|\vec{M}\right|d\varphi }[/math].
Для поворота, скажем, рычага вокруг фиксированной оси на угол [math]\displaystyle{ \varphi_2-\varphi_1 }[/math] получим
- [math]\displaystyle{ A = \int_{\varphi_1}^{\varphi_2} \left|\vec M\right| d\varphi = \left|\vec M\right| (\varphi_2-\varphi_1) = \left|\vec M\right|\int_{t_1}^{t_2} \omega(t)dt }[/math].
В системе СИ работа [math]\displaystyle{ A }[/math] измеряется в джоулях, угол — в радианах.
Размерность работы (и энергии) совпадает с размерностью момента силы («ньютон-метр» и джоуль — это одни и те же единицы). Момент силы 1 Н·м, при повороте рычага или вала на 1 радиан совершает работу в 1 Дж, а при повороте на один оборот совершает механическую работу и сообщает энергию [math]\displaystyle{ 2\pi }[/math] джоуля.
Измерение момента силы
Измерение момента силы осуществляется с помощью специальных приборов — торсиометров. Принцип их действия обычно основан на измерении угла закручивания упругого вала, передающего крутящий момент, либо на измерении деформации некоторого упругого рычага. Измерения деформации и угла закручивания производится различными датчиками деформации — тензометрическими, магнитоупругими, а также измерителями малых перемещений — оптическими, ёмкостными, индуктивными, ультразвуковыми, механическими.
Существуют специальные динамометрические ключи для измерения крутящего момента затягивания резьбовых соединений и регулируемые и нерегулируемые ограничители крутящего момента, так называемые «трещотки», применяемые в гаечных ключах, шуруповёртах, винтовых микрометрах и др.
Из истории понятия
Для того чтобы понять, откуда появилось понятие момента сил и как к нему пришли, стоит рассмотреть действие силы на рычаг, поворачивающийся относительно неподвижной оси. Работа, совершаемая при действии силы [math]\displaystyle{ \vec F }[/math] на рычаг [math]\displaystyle{ \vec r }[/math], совершающий вращательное движение вокруг неподвижной оси, может быть рассчитана исходя из следующих соображений.
Пусть под действием силы конец рычага смещается на бесконечно малый отрезок [math]\displaystyle{ dl }[/math], которому соответствует бесконечно малый угол [math]\displaystyle{ d\varphi }[/math]. Обозначим через [math]\displaystyle{ d\vec{l} }[/math] вектор, который направлен вдоль бесконечно малого отрезка [math]\displaystyle{ dl }[/math] и равен ему по модулю. Угол между векторами [math]\displaystyle{ \vec F }[/math] и [math]\displaystyle{ d\vec{l} }[/math] равен [math]\displaystyle{ \beta }[/math], а угол между векторами [math]\displaystyle{ \vec r }[/math] и [math]\displaystyle{ \vec F }[/math] равен [math]\displaystyle{ \alpha }[/math].
Следовательно, бесконечно малая работа [math]\displaystyle{ dA }[/math], совершаемая силой [math]\displaystyle{ \vec F }[/math] на бесконечно малом участке [math]\displaystyle{ dl }[/math], равна скалярному произведению вектора [math]\displaystyle{ d\vec{l} }[/math] и вектора силы, то есть [math]\displaystyle{ dA = \vec F \cdot d\vec{l} }[/math].
Теперь попытаемся выразить модуль вектора [math]\displaystyle{ d\vec{l} }[/math] через радиус-вектор [math]\displaystyle{ \vec r }[/math], а проекцию вектора силы [math]\displaystyle{ \vec F }[/math] на вектор [math]\displaystyle{ d\vec{l} }[/math] — через угол [math]\displaystyle{ \alpha }[/math].
Так как для бесконечно малого перемещения рычага [math]\displaystyle{ dl }[/math] можно считать, что траектория перемещения перпендикулярна рычагу [math]\displaystyle{ \vec r }[/math], используя соотношения для прямоугольного треугольника, можно записать следующее равенство: [math]\displaystyle{ dl = r \mathrm{tg}\,d\varphi }[/math], где в случае малого угла справедливо [math]\displaystyle{ \mathrm{tg}\,d\varphi = d\varphi }[/math] и, следовательно, [math]\displaystyle{ \left|d\vec{l}\right| = \left|\vec r\right| d\varphi }[/math].
Для проекции вектора силы [math]\displaystyle{ \vec F }[/math] на вектор [math]\displaystyle{ d\vec{l} }[/math] видно, что угол [math]\displaystyle{ \beta =\frac{\pi}{2} - \alpha }[/math], а так как [math]\displaystyle{ \cos{\left(\frac{\pi}{2} - \alpha\right)} = \sin\alpha }[/math], получаем, что [math]\displaystyle{ \left|\vec F\right|\cos\beta = \left|\vec F\right|\sin\alpha }[/math].
Теперь запишем бесконечно малую работу через новые равенства: [math]\displaystyle{ dA = \left|\vec r\right|d\varphi\left|\vec F\right|\sin\alpha }[/math], или [math]\displaystyle{ dA = \left|\vec r\right|\left|\vec F\right|\sin\alpha\, d\varphi }[/math].
Видно, что произведение [math]\displaystyle{ \left|\vec r\right|\left|\vec F\right|\sin\alpha }[/math] есть не что иное, как модуль векторного произведения векторов [math]\displaystyle{ \vec r }[/math] и [math]\displaystyle{ \vec F }[/math], то есть [math]\displaystyle{ \left|\vec r\times\vec F\right| }[/math], которое и было принято обозначить за момент силы [math]\displaystyle{ M }[/math], или модуль вектора момента силы [math]\displaystyle{ \left|\vec M\right| }[/math].
Теперь полная работа записывается просто: [math]\displaystyle{ A = \int\limits_0^\varphi \left|\vec r\times\vec F\right| d\varphi }[/math], или [math]\displaystyle{ A = \int\limits_0^\varphi \left|\vec M\right| d\varphi }[/math].
См. также
В статье не хватает ссылок на источники (см. также рекомендации по поиску). |

