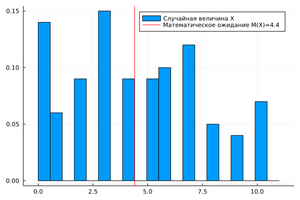
Математическое ожидание

Математи́ческое ожида́ние (en:Expected_value) — понятие в теории вероятностей, означающее среднее (взвешенное по вероятностям возможных значений) значение случайной величины. Математическое ожидание характеризует распределение вероятностей для случайной величины [math]\displaystyle{ X }[/math].

В случае непрерывной случайной величины подразумевается взвешивание по плотности распределения (более строгие определения см. ниже). Математическое ожидание случайного вектора равно вектору, компоненты которого равны математическим ожиданиям компонентов случайного вектора.

Обозначается через [math]\displaystyle{ \mathbb{E}[X] }[/math] (например, от англ. Expected value или нем. Erwartungswert); в русскоязычной литературе также встречается обозначение [math]\displaystyle{ M[X] }[/math] (возможно, от англ. Mean value или нем. Mittelwert, а возможно от «Математическое ожидание»). В статистике часто используют обозначение [math]\displaystyle{ \mu }[/math].

Для случайной величины, принимающей значения только 0 или 1 математическое ожидание равно [math]\displaystyle{ p }[/math] — вероятности «единицы». Математическое ожидание суммы таких случайных величин равно [math]\displaystyle{ np }[/math], где [math]\displaystyle{ n }[/math] — количество таких случайных величин. При этом вероятности появления определенного кол-ва единиц рассчитываются по биномиальному распределению. Поэтому в литературе, скорее всего, легче найти запись, что мат. ожидание биномиального распределения равно [math]\displaystyle{ np }[/math] .

Некоторые случайные величины не имеют математического ожидания, например, случайные величины, имеющие распределение Коши.

На практике математическое ожидание обычно оценивается как среднее арифметическое наблюдаемых значений случайной величины (выборочное среднее, среднее по выборке). Доказано, что при соблюдении определенных слабых условий (в частности, если выборка является случайной, то есть наблюдения являются независимыми) выборочное среднее стремится к истинному значению математического ожидания случайной величины при стремлении объема выборки (количества наблюдений, испытаний, измерений) к бесконечности.

Определение

Определение для дискретной случайной величины

Пример. Математическое ожидание случайной величины [math]\displaystyle{ X }[/math], принимающей значения [math]\displaystyle{ [0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10] }[/math] с разной вероятностью. Математическое ожидание [math]\displaystyle{ \mathbb{E}(X)=4,4 }[/math]

Если [math]\displaystyle{ X }[/math] — дискретная случайная величина, имеющая распределение

[math]\displaystyle{ \mathbb{P}(X=x_i) = p_i }[/math] , [math]\displaystyle{ \sum\limits_{i=1}^{\infty} p_i = 1 }[/math],

то прямо из определения интеграла Лебега следует, что

[math]\displaystyle{ \mathbb{E}[X]=\sum\limits_{i=1}^{\infty} x_i\, p_i }[/math].

Математическим ожиданием дискретной случайной величины называется сумма ряда при условии сходимости ряда.

Математическое ожидание целочисленной величины

• Если [math]\displaystyle{ X }[/math] — положительная целочисленная случайная величина (частный случай дискретной), имеющая распределение вероятностей

[math]\displaystyle{ \mathbb{P}(X=j) = p_j }[/math] , [math]\displaystyle{ j=0,1,\dotsc }[/math], [math]\displaystyle{ \sum\limits_{j=0}^{\infty} p_j = 1 }[/math],

то её математическое ожидание может быть выражено через производящую функцию последовательности [math]\displaystyle{ \{p_i\} }[/math]

[math]\displaystyle{ P(s)=\sum_{k=0}^\infty\;p_k s^k }[/math]

как значение первой производной в единице: [math]\displaystyle{ \mathbb{E}[X] = P'(1) }[/math]. Если математическое ожидание [math]\displaystyle{ X }[/math] бесконечно, то [math]\displaystyle{ \lim_{s\to 1}P'(s)=\infty }[/math] и мы будем писать [math]\displaystyle{ P'(1)=\mathbb{E}[X]=\infty }[/math]

Теперь возьмём производящую функцию [math]\displaystyle{ Q(s) }[/math] последовательности «хвостов» распределения [math]\displaystyle{ \{q_k\} }[/math]

[math]\displaystyle{ q_k=\mathbb{P}(X\gt k)=\sum_{j=k+1}^\infty{p_j} }[/math] , [math]\displaystyle{ Q(s)=\sum_{k=0}^\infty q_k s^k. }[/math]

Эта производящая функция связана с определённой ранее функцией [math]\displaystyle{ P(s) }[/math] свойством: [math]\displaystyle{ Q(s)=\frac{1-P(s)}{1-s} }[/math] при [math]\displaystyle{ |s|\lt 1 }[/math]. Из этого по теореме о среднем следует, что математическое ожидание равно просто значению этой функции в единице:

[math]\displaystyle{ \mathbb{E}[X]=P'(1)=Q(1) }[/math]

Общее определение через интеграл Лебега

Пусть задано вероятностное пространство [math]\displaystyle{ (\Omega,\mathfrak{A},\mathbb{P}) }[/math] и определённая на нём случайная величина [math]\displaystyle{ X }[/math]. То есть, по определению, [math]\displaystyle{ X\colon\Omega \to \mathbb{R} }[/math] — измеримая функция. Если существует интеграл Лебега от [math]\displaystyle{ X }[/math] по пространству [math]\displaystyle{ \Omega }[/math], то он называется математическим ожиданием, или средним (ожидаемым) значением и обозначается [math]\displaystyle{ M[X] }[/math] или [math]\displaystyle{ \mathbb{E}[X] }[/math].

[math]\displaystyle{ \mathbb{E}[X]=\int\limits_{\Omega}\! X(\omega)\, \mathbb{P}(d\omega). }[/math]

Определение через функцию распределения случайной величины

Если [math]\displaystyle{ F_X(x) }[/math] — функция распределения случайной величины, то её математическое ожидание задаётся интегралом Лебега — Стилтьеса:

[math]\displaystyle{ \mathbb{E}[X]=\int\limits_{-\infty}^{\infty}\!x\, dF_X(x) }[/math], [math]\displaystyle{ x \in \mathbb R }[/math].

Определение для абсолютно непрерывной случайной величины (через плотность распределения)

Математическое ожидание абсолютно непрерывной случайной величины, распределение которой задаётся плотностью [math]\displaystyle{ f_X(x) }[/math], равно

[math]\displaystyle{ \mathbb{E}[X]=\int\limits_{-\infty}^{\infty}\! x f_X(x)\, dx }[/math].

Математическое ожидание случайного вектора

Пусть [math]\displaystyle{ X=(X_1,\dots,X_n)^{\top}\colon\Omega \to \mathbb{R}^n }[/math] — случайный вектор. Тогда по определению

[math]\displaystyle{ \mathbb{E}[X]=(\mathbb{E}[X_1],\dots,\mathbb{E}[X_n])^{\top} }[/math],

то есть математическое ожидание вектора определяется покомпонентно.

Математическое ожидание преобразования случайной величины

Пусть [math]\displaystyle{ g\colon\mathbb{R}\to \mathbb{R} }[/math] — борелевская функция, такая что случайная величина [math]\displaystyle{ Y = g(X) }[/math] имеет конечное математическое ожидание. Тогда для него справедлива формула

[math]\displaystyle{ \mathbb{E}\left[g(X)\right] = \sum\limits_{i=1}^{\infty} g(x_i) p_i, }[/math]

если [math]\displaystyle{ X }[/math] имеет дискретное распределение;

[math]\displaystyle{ \mathbb{E}\left[g(X)\right] = \int\limits_{-\infty}^{\infty}\!g(x) f_X(x)\, dx, }[/math]

если [math]\displaystyle{ X }[/math] имеет абсолютно непрерывное распределение.

Если распределение [math]\displaystyle{ \mathbb{P}^X }[/math] случайной величины [math]\displaystyle{ X }[/math] общего вида, то

[math]\displaystyle{ \mathbb{E}\left[g(X)\right] = \int\limits_{-\infty}^{\infty}\!g(x)\, \mathbb{P}^X(dx). }[/math]

В специальном случае, когда [math]\displaystyle{ g(X) = X^k }[/math], математическое ожидание [math]\displaystyle{ \mathbb{E}[g(X)] = \mathbb{E}[X^k] }[/math] называется [math]\displaystyle{ k }[/math]-м моментом случайной величины.

Свойства математического ожидания

• Математическое ожидание числа (не случайной, фиксированной величины, константы) есть само число.

[math]\displaystyle{ \mathbb{E}[a] = a }[/math]

[math]\displaystyle{ a \in \mathbb{R} }[/math] — константа;

• Математическое ожидание линейно, то есть

[math]\displaystyle{ \mathbb{E}[aX+bY] = a\mathbb{E}[X]+b\mathbb{E}[Y] }[/math],

где [math]\displaystyle{ X,Y }[/math] — случайные величины с конечным математическим ожиданием, а [math]\displaystyle{ a,b\in \mathbb{R} }[/math] — произвольные константы;

В частности, математическое ожидание суммы (разности) случайных величин равно сумме (соответственно — разности) их математических ожиданий.

• Математическое ожидание сохраняет неравенства, то есть если [math]\displaystyle{ 0 \leqslant X \leqslant Y }[/math] почти наверняка, и [math]\displaystyle{ Y }[/math] — случайная величина с конечным математическим ожиданием, то математическое ожидание случайной величины [math]\displaystyle{ X }[/math] также конечно, и более того

[math]\displaystyle{ 0 \leqslant \mathbb{E}[X] \leqslant \mathbb{E}[Y] }[/math].

• Математическое ожидание не зависит от поведения случайной величины на событии вероятности нуль, то есть если [math]\displaystyle{ X = Y }[/math] почти наверняка, то

[math]\displaystyle{ \mathbb{E}[X]=\mathbb{E}[Y] }[/math].

• Математическое ожидание произведения двух независимых или некоррелированных случайных величин [math]\displaystyle{ X,Y }[/math] равно произведению их математических ожиданий

[math]\displaystyle{ \mathbb{E}[XY] = \mathbb{E}[X]\cdot \mathbb{E}[Y] }[/math].

Неравенства, связанные с математическим ожиданием

Неравенство Маркова — для неотрицательной случайной величины [math]\displaystyle{ X\colon \Omega \to \mathbb{R}^+ }[/math] определённой на вероятностном пространстве [math]\displaystyle{ (\Omega, \mathcal{F},\mathbb{P}) }[/math] с конечным математическим ожиданием [math]\displaystyle{ \mathbb{E}(X) }[/math] выполняется неравенство:

[math]\displaystyle{ \mathbb{P}\left(X \geqslant a\right) \leqslant \frac{\mathbb{E}(X)}{a} }[/math], где [math]\displaystyle{ a\gt 0 }[/math].

Неравенство Йенсена для математического ожидания выпуклой функции от случайной величины. Пусть [math]\displaystyle{ (\Omega,\mathcal{F},\mathbb{P}) }[/math] — вероятностное пространство, [math]\displaystyle{ X\colon\Omega\to \mathbb{R} }[/math] — определённая на нём случайная величина, [math]\displaystyle{ \varphi\colon\mathbb{R} \to \mathbb{R} }[/math] — выпуклая борелевская функция, такие, что [math]\displaystyle{ X, \varphi(X) \in L^1(\Omega,\mathcal{F},\mathbb{P}) }[/math], то

[math]\displaystyle{ \varphi(\mathbb{E}(X)) \leqslant \mathbb{E}(\varphi(X)) }[/math].

Теоремы, связанные с математическим ожиданием

• Теорема Леви о монотонной сходимости.
• Теорема Лебега о мажорируемой сходимости: пусть есть сходящаяся почти всюду последовательность случайных величин: [math]\displaystyle{ X_n\to X }[/math]. Пусть в дополнение существует интегрируемая случайная величина [math]\displaystyle{ Y }[/math], такая что [math]\displaystyle{ \forall n\in\N\quad|X_n|\leqslant Y }[/math] почти наверное. Тогда случайные величины [math]\displaystyle{ X_n,\;X }[/math] интегрируемы и

[math]\displaystyle{ \lim\limits_{n\to\infty}\mathbb{E}(X_n)=\mathbb{E}(X) }[/math] .

• Тождество Вальда: для независимых одинаково распределённых случайных величин [math]\displaystyle{ X_1,...,X_N }[/math], где [math]\displaystyle{ N }[/math] является положительной целочисленной случайной величиной, независимой от [math]\displaystyle{ X_i }[/math], при условии, что [math]\displaystyle{ X_i }[/math] и [math]\displaystyle{ N }[/math] имеют конечное математическое ожидание, будет выполняться следующее равенство:

[math]\displaystyle{ \mathbb{E}\left(\sum_{i=1}^{N}X_i\right)=\mathbb{E}(N)\mathbb{E}(X) }[/math]

• Математическое ожидание случайной величины [math]\displaystyle{ X }[/math] равно значению первой производной её производящей функции моментов [math]\displaystyle{ G(u) }[/math] в точке 0:

[math]\displaystyle{ \mathbb{E}(X) = G'(0) }[/math].

Примеры

• Пусть случайная величина имеет дискретное равномерное распределение, то есть [math]\displaystyle{ \mathbb{P}(X = x_i) = \frac{1}{n},\; i=1,\ldots, n. }[/math] Тогда её математическое ожидание

[math]\displaystyle{ \mathbb{E}[X] = \frac{1}{n} \sum\limits_{i=1}^n x_i }[/math]

равно среднему арифметическому всех принимаемых значений.

• Пусть случайная величина имеет непрерывное равномерное распределение на интервале [math]\displaystyle{ [a,b] }[/math], где [math]\displaystyle{ a\lt b }[/math]. Тогда её плотность имеет вид [math]\displaystyle{ f_X(x) = \frac{1}{b-a} \mathbf{1}_{[a,b]}(x) }[/math] и математическое ожидание равно

[math]\displaystyle{ \mathbb{E}[X] = \int\limits_{a}^b\!\frac{x}{b-a}\, dx = \frac{a+b}{2} }[/math].

• Пусть случайная величина [math]\displaystyle{ X }[/math] имеет стандартное распределение Коши. Тогда

[math]\displaystyle{ \int\limits_{-\infty}^{\infty}\!xf_X(x)\, dx = \infty }[/math],

то есть математическое ожидание [math]\displaystyle{ X }[/math] не определено.

См. также

• Дисперсия случайной величины
• Моменты случайной величины
• Условное математическое ожидание

Литература

• Феллер В. Глава XI. Целочисленные величины. Производящие функции // Введение в теорию вероятностей и её приложения = An introduction to probability theory and its applicatons, Volume I second edition / Перевод с англ. Р. Л. Добрушина, А. А. Юшкевича, С. А. Молчанова Под ред. Е. Б. Дынкина с предисловием А. Н. Колмогорова. — 2-е изд. — М.: Мир, 1964. — С. 270—272.