Квантовая механика

Волновые функции электрона в атоме водорода на разных энергетических уровнях. Квантовая механика не может предсказать точное местоположение частицы в пространстве, а только вероятность её обнаружения в разных малых окрестностях точки пространства. Более яркие области представляют более высокую вероятность обнаружения электрона.

Ква́нтовая (волнова́я) меха́ника — фундаментальная физическая теория, которая описывает природу в масштабе атомов и субатомных частиц. Она лежит в основании всей квантовой физики, включая квантовую химию, квантовую теорию поля, квантовую технологию и квантовую информатику.

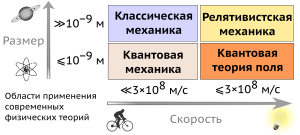
Классическая физика, совокупность теорий, существовавших до появления квантовой механики, описывает многие аспекты природы в обычном (макроскопическом) масштабе, но недостаточна для их количественного описания в малых (атомных и субатомных) масштабах. Большинство теорий классической физики можно вывести из квантовой механики как приближения, справедливые в больших (макроскопических) масштабах.

Квантовая механика отличается от классической физики тем, что энергия, импульс, угловой момент и другие величины связанного состояния системы не могут принимать произвольные значения, но ограничены дискретными значениями (квантование), объекты обладают характеристиками как частиц, так и волн (корпускулярно-волновой дуализм), и существуют пределы нашей возможности точно предсказать значение физической величины до её измерения при заданном полном наборе начальных условий (принцип неопределенности).

Квантовая механика постепенно возникла из теорий, объясняющих наблюдения, которые не могли быть согласованы с понятиями классической физики, таких как решение Макса Планка в 1900 году проблемы излучения абсолютно чёрного тела и соответствие между энергией и частотой кванта света в статье Альберта Эйнштейна 1905 года, которая объяснила фотоэффект. Эти ранние попытки понять микроскопические явления, теперь известные как «старая квантовая теория», привели к стремительному развитию квантовой механики в середине 1920-х годов в работах Нильса Бора, Эрвина Шрёдингера, Вернера Гейзенберга, Макса Борна и других. Современная теория формулируется с использованием различных специально разработанных математических формализмов. В одном из них математическая сущность, называемая волновой функцией, предоставляет информацию в виде амплитуд вероятности о том, к чему приводят измерения энергии, импульса и других физических свойств частицы.

Обзор и основные понятия

Квантовая механика позволяет рассчитывать свойства и поведение физических систем. Обычно её применяют к микроскопическим системам: молекулам, атомам и субатомным частицам. Также было показано, что квантовая механика верно описывает поведение сложных молекул с тысячами атомов, хотя при попытке применить её к людям возникают философские вопросы и парадоксы, такие как друг Вигнера, и её применение ко Вселенной в целом также остаётся спекулятивным. Предсказания квантовой механики были подтверждены экспериментально с чрезвычайно высокой степенью точности.

Фундаментальной особенностью квантовой теории является то, что она обычно не может с определённостью предсказать значения физических величин (динамических переменных), а только даёт вероятности их измерения. Математически вероятность находится путём возведения в квадрат абсолютного значения комплексного числа, известного как амплитуда вероятности. Это утверждение известно как правило Борна, названное в честь физика Макса Борна. Например, квантовая частица, такая как электрон, описывается волновой функцией, которая задаёт для каждой точки пространства амплитуду вероятности. Применение правила Борна к этим амплитудам определяет функцию плотности вероятности для координаты частицы, когда будет проведён эксперимент по её измерению. Это лучшее, что может дать теория; нельзя точно сказать, где будет найден электрон. Уравнение Шрёдингера описывает эволюцию системы во времени, то есть связывает набор амплитуд вероятности, относящихся к одному моменту времени, с набором амплитуд вероятностей, относящихся к другому моменту времени.

Одним из следствий математических правил квантовой механики является компромисс при попытке определить различные измеримые величины. Самая известная форма такого компромисса — принципа неопределенности гласит, что как бы ни было приготовлено состояние квантовой частицы, или как бы тщательно ни были поставлены над этой частицей опыты, при измерении невозможно точное предсказание значений её положения и импульса в один момент времени.

Ещё одним следствием математических правил квантовой механики является квантовая интерференция, в качестве примера которой рассматривается опыт с двумя щелями. В базовом варианте этого эксперимента когерентный источник света, например лазер, освещает непрозрачную пластину, с прорезанными двумя параллельными щелями, и свет, проходящий через щели, наблюдается на экране позади пластины. Волновая природа света означает, что световые волны проходят через две щели, интерферируя и создавая на экране яркие и тёмные полосы — результат, которого нельзя было бы ожидать, если бы свет состоял из классических частиц. Однако опыт всегда показывает, что свет поглощается экраном в отдельных точках в виде отдельных частиц, а не волн; интерференционная картина проявляется из-за различной плотности засветки фотографической пластины при попадании этих частиц на экран. Кроме того, в других вариациях опыта, включающих детекторы в щелях, обнаруживают, что каждый наблюдаемый фотон проходит через одну щель (как классическая частица), а не через обе щели (как волна). Из таких экспериментов следует вывод, что частицы не образуют интерференционную картину, если определить, через какую щель они проходят. Было обнаружено, что другие объекты атомного масштаба, такие как электроны, демонстрируют такое же поведение, когда падают на экран с двумя щелями. Такое поведение микрообъектов известно как корпускулярно-волновой дуализм — он «лежит в сердце» квантовой механики.

Туннельный эффект — квантовая механика показывает, что электроны могут преодолеть потенциальный барьер, что подтверждается результатами экспериментов.
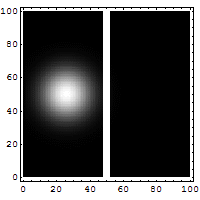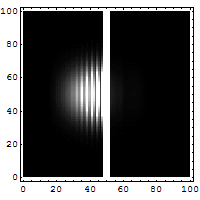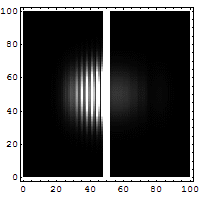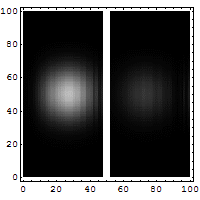
Классическая механика, наоборот, предсказывает, что это невозможно

Ещё одно противоречащее повседневному опыту явление, предсказанное квантовой механикой — квантовое туннелирование, когда частица, столкнувшись с потенциальным барьером, может преодолеть его, даже если её кинетическая энергия меньше максимума потенциала. В классической механике эта частица отражается всегда от барьера. Квантовое туннелирование имеет несколько важных наблюдаемых последствий, включающих радиоактивный распад, ядерный синтез в звёздах и такие приложения, как сканирующая туннельная микроскопия и создание туннельных диодов.

Когда квантовые системы взаимодействуют, результатом может быть создание квантовой запутанности: их свойства становятся настолько переплетёнными, что описание целого исключительно в терминах отдельных частей больше невозможно. Шрёдингер назвал запутывание

«… характерная черта квантовой механики — полный отход от классических путей понимания»

Оригинальный текст (англ.)[показатьскрыть]

„… the characteristic trait of quantum mechanics, the one that enforces its entire departure from classical lines of thought“

Квантовая запутанность реализует нелогичные свойства квантовой псевдотелепатии и может оказаться ценным методом в протоколах связи, таких как квантовое распределение ключей и сверхплотное кодирование. Вопреки распространённому заблуждению, запутанность не позволяет посылать сигналы быстрее скорости света, что демонстрирует теорема об отсутствии связи.

Другая возможность, открываемая запутанностью, — это проверка «скрытых переменных», гипотетических свойств, более фундаментальных, чем величины, рассматриваемые в самой квантовой теории, знание которых позволило бы делать более точные предсказания, чем может дать квантовая теория. Множество полученных результатов, в первую очередь теорема Белла, продемонстрировало, что широкие классы таких теорий со скрытыми переменными на самом деле несовместимы с квантовой физикой. Согласно теореме Белла, если природа действительно описывается какой-либо теорией локальных скрытых переменных, то результаты проверки неравенств Белла будут ограничены определённым образом, поддающимся количественной оценке. Было проведено множество тестов Белла с использованием запутанных частиц, и они показали результаты, несовместимые с ограничениями, налагаемыми теориями с локальными скрытыми переменными.

Невозможно представить эти понятия более чем поверхностно, не вводя при этом фактическую математику; понимание квантовой механики требует не только манипулирования комплексными числами, но и линейной алгебры, дифференциальных уравнений, теории групп и других более сложных областей математики. Физик Джон К. Баэз предупреждает:

«… нельзя понять интерпретацию квантовой механики, не умея решать задачи квантовой механики — чтобы понять эту теорию, нужно уметь использовать её (и наоборот).»

Оригинальный текст (англ.)[показатьскрыть]

„… there’s no way to understand the interpretation of quantum mechanics without also being able to solve quantum mechanics problems — to understand the theory, you need to be able to use it (and vice versa)“.

Карл Саган обрисовал в общих чертах «математическое обоснование» квантовой механики и написал:

«Для большинства студентов-физиков это может занять у них период, скажем, от третьего класса до начала аспирантуры — примерно 15 лет. (…) Объём работы популяризатора науки, чтобы попытаться донести какое-то представление о квантовой механике до широкой аудитории, не прошедшей через этот обряд инициации, пугает. Действительно, на мой взгляд, нет успешного популярного изложения квантовой механики — отчасти по этой причине.»

Оригинальный текст (англ.)[показатьскрыть]

„For most physics students, this might occupy them from, say, third grade to early graduate school – roughly 15 years. […] The job of the popularizer of science, trying to get across some idea of quantum mechanics to a general audience that has not gone through these initiation rites, is daunting. Indeed, there are no successful popularizations of quantum mechanics in my opinion – partly for this reason.“

Соответственно, в этой статье будет представлена математическая формулировка квантовой механики и рассмотрено её применение на некоторых полезных и часто изучаемых примерах.

История

Основные статьи: История возникновения квантовой физики и Атомная теория

Макс Планк считается отцом квантовой теории.

Сольвеевская конференция 1927 года в Брюсселе стала пятой всемирной конференцией по физике.

Квантовая механика была разработана в первые десятилетия 20-го века из-за необходимости объяснить явления, которые не нашли объяснения в рамках классического подхода. Научные исследования волновой природы света начались в XVII и XVIII веках, когда такие учёные, как Роберт Гук, Христиан Гюйгенс и Леонард Эйлер, предложили волновую теорию света, основанную на экспериментальных наблюдениях. В 1803 году английский эрудит Томас Янг описал знаменитый эксперимент с двумя щелями. Этот эксперимент сыграл важную роль в общем признании волновой теории света.

В начале 19 века химические исследования Джона Дальтона и Амедео Авогадро придали вес атомной теории материи, идее, на которой Джеймс Клерк Максвелл, Людвиг Больцман и другие построили кинетическую теорию газов. Успехи кинетической теории ещё больше укрепили веру в идею о том, что материя состоит из атомов, однако у этой теории также были недостатки, которые можно было устранить только с развитием квантовой механики. В то время как ранняя концепция атомов из греческой философии состояла в том, что они были неделимыми единицами – слово «атом» происходит от греческого «неразрезаемый» — в XIX веке были сформулированы гипотезы о субатомной структуре. Одним из важных открытий в этом отношении было наблюдение Майклом Фарадеем в 1838 году свечения, вызванного электрическим разрядом внутри стеклянной трубки, содержащей газ при низком давлении. Юлиус Плюккер, Иоганн Вильгельм Гитторф и Ойген Гольдштейн продолжили и усовершенствовали работу Фарадея, что привело к идентификации катодных лучей, которые, как обнаружил Дж. Дж. Томсон, состоят из субатомных частиц, названных впоследствии электронами.

Проблема излучения чёрного тела была открыта Густавом Кирхгофом в 1859 году. В 1900 году Макс Планк выдвинул гипотезу о том, что энергия излучается и поглощается дискретными «квантами» (или энергетическими пакетами). Это позволило объяснить наблюдаемый спектр излучения абсолютно чёрного тела. Слово «квант» происходит от латинского, что означает «сколько». Согласно Планку, количество энергии можно рассматривать как разделённое на «элементы», величина которых (E) будет пропорциональна их частоте (ν):

[math]\displaystyle{ E = h \nu\ }[/math] ,

где h — постоянная Планка. Планк осторожно настаивал на том, что это лишь аспект процессов поглощения и испускания излучения, а не физическая реальность излучения. На самом деле он не мог выбрать считать ли свою квантовую гипотезу математическим трюком для получения правильного ответа, или значительным открытием. Однако в 1905 году Альберт Эйнштейн реалистично интерпретировал квантовую гипотезу Планка и использовал её для объяснения фотоэлектрического эффекта, при котором свет, падающий на определённые материалы, может выбивать электроны из материала. Затем Нильс Бор развил идеи Планка об излучении включив её в модель атома водорода, которая успешно предсказала спектральные линии водорода. Эйнштейн развил эту идею, чтобы показать, что электромагнитная волна, такая как свет, также может быть описана как частица (позже названная фотоном) с дискретным количеством энергии, которое зависит от его частоты. В своей статье «Квантовая теория излучения» (англ. On the Quantum Theory of Radiation) Эйнштейн расширил взаимосвязь между энергией и материей, чтобы объяснить поглощение и испускание энергии атомами. Хотя в то время его общая теория относительности затмила эту идею, в этой статье был сформулирован механизм, лежащий в основе стимулированного излучения, который стал основным принципом работы лазеров.

Эта фаза развития квантовой теории известна как старая квантовая теория. Она никогда не была полной и непротиворечивой, и была скорее набором эвристических поправок к классической механике . Старая теория теперь понимается как полуклассическое приближение к современной квантовой механике. Заметные результаты этого периода включают, помимо работ Планка, Эйнштейна и Бора, упомянутых выше, работы Эйнштейна и Петера Дебая по удельной теплоёмкости твёрдых тел, доказательство Бора и Хендрики Йоханны ван Леувен, что классическая физика не может объяснить диамагнетизм и расширение Арнольдом Зоммерфельдом модели Бора, включающее релятивистские эффекты.

В середине 1920-х годов была разработана квантовая механика, ставшая стандартной формулировкой атомной физики. В 1923 году французский физик Луи де Бройль выдвинул теорию волн материи, заявив, что частицы могут проявлять волновые характеристики и наоборот. Основанная на подходе де Бройля, современная квантовая механика родилась в 1925 году, когда немецкие физики Вернер Гейзенберг, Макс Борн и Паскуаль Йордан разработали матричную механику, а австрийский физик Эрвин Шрёдингер изобрёл волновую механику. Борн представил вероятностную интерпретацию волновой функции Шрёдингера в июле 1926 года. Таким образом, возникла целая область квантовой физики, что привело к её более широкому признанию на Пятой Сольвеевской конференции в 1927 году.

В 1927 году В. Гайтлер и Ф. Лондон рассчитали спектр молекулы водорода и объяснили возникновение химической связи в молекулах. Ф. Блох заложил основы движения частиц в периодическом потенциале кристаллической решётки. В том же году В. Паули обобщил уравнение Шрёдингера с учётом спина электрона, а в следующем году появилось релятивистское уравнение для электрона — уравнение Дирака, которое предсказало существование античастиц.

Эйнштейн не признавал квантовую механику как законченную теорию, то есть теорию, которая полностью описывает природу. Поэтому в 1935 году появилась статья о парадоксе возникающем в запутанной системе, который сейчас называется парадоксом Эйнштейна — Подольского — Розена. Шрёдингер поддержал идею ЭПР и придумал шрёдингеровского кота. Эти парадоксы привлекают внимание исследователей основ квантовой механики.

Решение уравнения Шрёдингера для атома водорода имеет аналитическую форму, но для многоэлектронного атома решение не известно, и возникают различные приближённые методы вычисления волновых функций. Например, в 1928 году метод самосогласованного поля предложил Д. Хартри, а в 1930 году В. А. Фок расширил этот подход с учётом спина электрона.

К 1930 году квантовая механика была дополнительно унифицирована и формализована Давидом Гильбертом, Полом Дираком и Джоном фон Нейманом с большим упором на формализацию процесса измерения, статистическую природу нашего знания о реальности и философские рассуждения о «наблюдателе». С тех пор она проникла во многие дисциплины, включая квантовую химию, квантовую электронику, квантовую оптику и квантовую информатику. Она также объясняет особенности современной периодической таблицы элементов и описывает поведение атомов во время образования химической связи и ток электронов в полупроводниках, и поэтому играет решающую роль во многих современных технологиях. Хотя квантовая механика была создана для описания мира очень на очень маленьких масштабов, она также необходима для объяснения некоторых макроскопических явлений, таких как сверхпроводники и сверхтекучие жидкости. Теорию сверхпроводников первого рода построили Д. Бардин Л. Купер и Шриффер в 1957 году.

В 1954 году благодаря работам Ч. Таунса, Н. Г. Басова и А. М. Прохорова появились первые микроволновые генераторы — мазеры на аммиаке. Для усиления излучения в оптическом диапазоне использовался рубин Т. Мейманом в 1960 году. В 1963 году Ж. Алфёров создал первые полупроводниковые гетероструктуры, на основе которых создаются современные полупроводниковые лазеры.

В 1980 году Пол Бениофф описал первую квантово-механическую модель компьютера. В этой работе П. Бениофф показал, что компьютер может работать в соответствии с законами квантовой механики, использовав уравнение Шредингера для описания машин Тьюринга, заложив основу для дальнейшей работы в области квантовых вычислений. Первая экспериментальная демонстрация двух-кубитного квантового компьютера, работающего на явлении ядерного магнитного резонанса сообшалась в 1998 году. В октябре 2019 года компания Google объявила, что ей удалось построить 53-кубитный сверхпроводящий квантовый процессор Sycamore и продемонстрировать «квантовое превосходство» над обычными компьютерами.

Математическая формулировка

Основная статья: Математические основы квантовой механики

В математически строгой формулировке квантовой механики состояние квантовомеханической системы представляет собой вектор [math]\displaystyle{ \psi }[/math] заданный в комплексном (сепарабельном) гильбертовом пространстве [math]\displaystyle{ \mathcal H }[/math]. Постулируется, что этот вектор нормирован относительно скалярного произведения гильбертова пространства, то есть подчиняется условию [math]\displaystyle{ \langle \psi,\psi \rangle = 1 }[/math], и он корректно определён с точностью до комплексного числа по модулю 1 (глобальной фазы), или, другими словами, состояния [math]\displaystyle{ \psi }[/math] и [math]\displaystyle{ e^{i\alpha}\psi }[/math] представляют собой одну и ту же физическую систему. Возможные состояния — это точки проективного гильбертова пространства, обычно называемого комплексным проективным пространством. Точная природа этого гильбертова пространства зависит от рассматриваемой системы — например, для описания координаты и импульса частицы, гильбертово пространство — это пространство комплексных функций, интегрируемых с квадратом [math]\displaystyle{ L^2(\mathbb C) }[/math], а гильбертово пространство для спина одиночной частицы — это просто пространство двумерных комплексных векторов [math]\displaystyle{ \mathbb C^2 }[/math] с обычным скалярным произведением.

Интересующие физические величины — координата, импульс, энергия, спин — представлены наблюдаемыми величинами (или просто наблюдаемыми), которым поставлены в соответствие эрмитовые (точнее, самосопряженные) линейные операторы, действующие в гильбертовом пространстве. Квантовое состояние может быть собственным вектором для оператора наблюдаемой, или собственным состоянием, а связанное с ним собственное значение соответствует значению наблюдаемой в этом собственном состоянии. В более общем смысле квантовое состояние задаётся линейной комбинацией собственных состояний, известной как квантовая суперпозиция. При измерении наблюдаемой, результатом будет одно из её дискретных собственных значений с вероятностью, заданной правилом Борна: в простейшем случае собственное значение [math]\displaystyle{ \lambda }[/math] является невырожденным, а вероятность определяется выражением [math]\displaystyle{ |\langle \vec\lambda,\psi\rangle|^2 }[/math], где [math]\displaystyle{ \vec\lambda }[/math] — его собственный вектор. В более общем случае собственное значение вырождено, а вероятность определяется выражением [math]\displaystyle{ \langle \psi,P_\lambda\psi\rangle }[/math], где [math]\displaystyle{ P_\lambda }[/math] — проектор на связанное с ним собственное пространство. В случае, когда рассматривается непрерывный спектр собственных значений эти формулы используют понятие плотности вероятности.

После измерения, если получен результат [math]\displaystyle{ \lambda }[/math], то постулируется, что квантовое состояние коллапсирует до [math]\displaystyle{ \vec\lambda }[/math], в невырожденном случае, или [math]\displaystyle{ P_\lambda\psi/\sqrt{\langle \psi,P_\lambda\psi\rangle} }[/math], в общем случае. Таким образом, вероятностный характер квантовой механики проистекает из процесса измерения. Это один из самых сложных для понимания физических аспектов квантовых систем. Эта тема была центральным вопросом знаменитых дебатов Бора и Эйнштейна, в которых два учёных пытались прояснить эти фундаментальные принципы с помощью мысленных экспериментов. В течение десятилетий после формулировки квантовой механики широко изучался вопрос о том, что представляет собой «измерение». Были сформулированы более современные интерпретации квантовой механики, которые избавляются от концепции «редукции (коллапса) волновой функции» (см., например, многомировая интерпретация). Основная идея заключается в том, что когда квантовая система взаимодействует с измерительным прибором, их соответствующие волновые функции запутываются, так что исходная квантовая система перестаёт существовать как независимая сущность. Подробнее см. в статье об измерении в квантовой механике.

Эволюция квантового состояния во времени описывается уравнением Шрёдингера:

[math]\displaystyle{ i\hbar {\frac {d}{dt}} \psi (t) =H \psi (t)\,. }[/math]

Здесь [math]\displaystyle{ H }[/math] — гамильтониан системы, или оператор наблюдаемой, соответствующей полной энергии системы, и [math]\displaystyle{ \hbar }[/math] — приведённая постоянная Планка. Постоянная [math]\displaystyle{ i\hbar }[/math] вводится так, что гамильтониан сводится к классическому гамильтониану в случаях, когда квантовая система близка по своим свойствам к соответствующей классической модели; возможность сделать такое приближение в определённом пределе называется принципом соответствия.

Формальное решение этого дифференциального уравнения задаётся выражением

[math]\displaystyle{ \psi(t) = e^{-iHt/\hbar }\psi(0)\,. }[/math]

Оператор [math]\displaystyle{ U(t) = e^{-iHt/\hbar } }[/math] известен как оператор эволюции и обладает важным свойством унитарности. На этот раз эволюция детерминирована в том смысле, что если задано начальное квантовое состояние [math]\displaystyle{ \psi(0) }[/math], то этот оператор даёт определённое предсказание того, какое квантовое состояние [math]\displaystyle{ \psi(t) }[/math] будет в любой другой последующий момент времени.

Плотности вероятностей, соответствующие волновым функциям электрона в атоме водорода, обладающим определёнными энергетическими уровнями (возрастающими от верхней части изображения до нижней части: n = 1, 2, 3, …) и угловыми моментами (возрастающие слева направо: s, p, d, . . .). Более плотные области соответствуют более высокой плотности вероятности при измерении положения. Такие волновые функции прямо сравнимы с фигурами Хладни акустических мод колебаний в классической физике и также являются модами колебаний, обладающими определённой энергией и, соответствующей ей частотой. Угловой момент и энергия квантованы и принимают только дискретные значения, подобные показанным (как в случае с резонансными частотами в акустике).

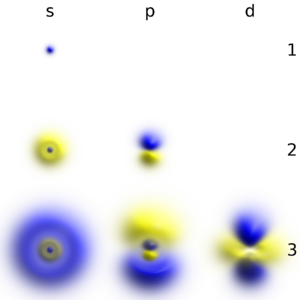
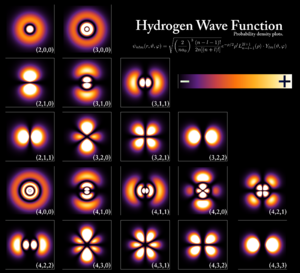
Некоторые волновые функции описывают распределения вероятностей, которые не зависят от времени, такие как собственные состояния гамильтониана. Многие динамические системы, рассматриваемые в классической механике, описываются такими «стационарными» волновыми функциями. Например, один электрон в невозбуждённом атоме классически изображается как частица, движущаяся по круговой траектории вокруг ядра атома, тогда как в квантовой механике он описывается стационарной волновой функцией, окружающей ядро. Например, волновая функция электрона для невозбуждённого атома водорода представляет собой сферически-симметричную функцию, известную как s-орбиталь.

Аналитические решения уравнения Шрёдингера известны для очень немногих относительно простых модельных гамильтонианов, включающих квантовый гармонический осциллятор, частицу в ящике, молекулярный ион водорода, атом водорода и другие. Даже атом гелия, который содержит всего два электрона бросил вызов всем попыткам построить полностью аналитическое решение.

Существуют методы нахождения приближённых решений. Один метод, называемый теорией возмущений, использует аналитический результат для простой квантовомеханической модели, чтобы построить решение для родственной, но более сложной модели, например, путём добавления малой потенциальной энергии. Другой метод называется «квазиклассическим уравнением движения» и применяется к системам, для которых квантовая механика даёт лишь небольшие отклонения от классического поведения. Эти отклонения можно вычислить на основе классического движения. Этот подход особенно важен в области квантового хаоса.

Принцип неопределенности

Основная статья: Принцип неопределенности

Одним из следствий формализма квантовой механики является принцип неопределенности. В своей наиболее известной форме он утверждает, что для квантовой частицы нельзя одновременно точно предсказать её координату и импульс. Координата и импульс являются наблюдаемыми, то есть они представимы в виде эрмитовых операторов. Оператор координаты [math]\displaystyle{ \hat{X} }[/math] и оператор импульса [math]\displaystyle{ \hat{P} }[/math] не коммутируют друг с другом, а удовлетворяют каноническому коммутационному соотношению:

[math]\displaystyle{ [\hat{X}, \hat{P}] = i\hbar\,. }[/math]

При заданном квантовом состоянии правило Борна позволяет вычислить математические ожидания для [math]\displaystyle{ X }[/math] и [math]\displaystyle{ P }[/math], и их степеней. Задавая неопределённость наблюдаемой по формуле стандартного отклонения, можно записать для координаты

[math]\displaystyle{ \sigma_X=\sqrt{\langle {X}^2 \rangle-\langle {X}\rangle^2}\,, }[/math]

и аналогично для импульса:

[math]\displaystyle{ \sigma_P=\sqrt{\langle {P}^2 \rangle-\langle {P}\rangle^2}\,. }[/math]

Принцип неопределённости гласит, что

[math]\displaystyle{ \sigma_X \sigma_P \geq \frac{\hbar}{2}\,. }[/math]

Любое стандартное отклонение в принципе можно сделать сколь угодно малым, но не обе величины одновременно. Это неравенство обобщается на произвольные пары самосопряжённых операторов [math]\displaystyle{ A }[/math] и [math]\displaystyle{ B }[/math]. Коммутатор этих двух операторов по определению равен

[math]\displaystyle{ [A,B]=AB-BA, }[/math]

что задаёт нижнюю границу произведения стандартных отклонений:

[math]\displaystyle{ \sigma_A \sigma_B \geq \frac{1}{2}\left|\langle[A,B]\rangle \right|. }[/math]

Из канонического коммутационного соотношения следует, что операторы координаты и импульса являются преобразованиями Фурье друг друга. Описание объекта в импульсном пространстве задаётся преобразованием Фурье его координатного описания. Тот факт, что зависимость от импульса является преобразованием Фурье координатной зависимости, означает, что оператор импульса эквивалентен (с точностью до [math]\displaystyle{ i/\hbar }[/math] множителя) взятию производной по координате, так как в анализе Фурье операции дифференцирования соответствует умножение в двойственном пространстве. Поэтому в квантовых уравнениях в координатном представлении импульс [math]\displaystyle{ p_i }[/math] заменяется выражением [math]\displaystyle{ -i \hbar \frac {\partial}{\partial x} }[/math], и, в частности, в нерелятивистском уравнении Шрёдингера в координатном пространстве квадрат импульса заменён умноженным на [math]\displaystyle{ -\hbar^2 }[/math] лапласианом.

Составные системы и запутанность

Основная статья: Квантовая запутанность

Когда две разные квантовые системы рассматриваются вместе, гильбертово пространство объединённой системы представляет собой тензорное произведение гильбертовых пространств двух компонент. Например, пусть A и B — две квантовые системы с гильбертовыми пространствами [math]\displaystyle{ \mathcal H_A }[/math] и [math]\displaystyle{ \mathcal H_B }[/math] соответственно. Тогда гильбертово пространство составной системы равно

[math]\displaystyle{ \mathcal H_{AB} = \mathcal H_A \otimes \mathcal H_B. }[/math]

Если состояние для первой системы есть вектор [math]\displaystyle{ \psi_A }[/math], а состояние для второй системы — [math]\displaystyle{ \psi_B }[/math], то состояние составной системы равно

[math]\displaystyle{ \psi_A \otimes \psi_B. }[/math]

Не все состояния в совместном гильбертовом пространстве [math]\displaystyle{ \mathcal H_{AB} }[/math] можно записать в такой форме, потому что принцип суперпозиции подразумевает, что линейные комбинации этих «разделимых» или «составных» состояний также возможны. Например, если [math]\displaystyle{ \psi_A }[/math] и [math]\displaystyle{ \phi_A }[/math] оба возможных состояния системы [math]\displaystyle{ A }[/math], и [math]\displaystyle{ \psi_B }[/math] и [math]\displaystyle{ \phi_B }[/math] — возможные состояния системы [math]\displaystyle{ B }[/math], тогда новое состояние

[math]\displaystyle{ \tfrac{1}{\sqrt{2}} \left ( \psi_A \otimes \psi_B + \phi_A \otimes \phi_B \right ) }[/math]

описывает допустимое совместное состояние, которое не является разделимым. Состояния, которые не являются разделимыми, называются запутанными или сцепленными.

Если состояние составной системы запутано, то ни компонентную систему A ни систему B невозможно описать вектором состояния. Вместо этого можно определить матрицы плотности подсистемы, которые описывают результаты, которые можно получить, выполняя измерения только над любым из компонент системы. Однако это неизбежно приводит к потере информации: знания матриц плотности отдельных систем недостаточно для восстановления состояния составной системы. Точно так же, как матрицы плотности определяют состояние подсистемы более крупной системы. Аналогичным образом положительные операторнозначные меры (POVM) описывают влияние на подсистему измерения, выполненного в более крупной системе. POVM широко используются в квантовой теории информации.

Как описано выше, запутанность — это ключевая особенность моделей процесса измерения, в котором детектор запутывается с измеряемой системой. Системы, взаимодействующие с окружающей средой, в которой они находятся, обычно запутываются с этой средой — явление, известное как квантовая декогеренция. Оно может объяснить, почему на практике квантовые эффекты трудно наблюдать в макроскопических системах.

Эквивалентность формулировок

Существует множество математически эквивалентных формулировок квантовой механики. Одной из старейших и наиболее распространённых является «теория преобразований», предложенная Полем Дираком, которая объединяет и обобщает две самые ранние формулировки квантовой механики — матричную механику (изобретена Вернером Гейзенбергом) и волновую механику (изобретена Эрвином Шредингером). Альтернативно, квантовую механику можно сформулировать на языке интеграла по траекториям Фейнмана, в которой квантовомеханическая амплитуда рассматривается как сумма всех возможных классических и неклассических путей между начальным и конечным состояниями, что представляется собой квантовомеханический аналог принципа действия в классической механике.

Симметрии и законы сохранения

Основная статья: Теорема Нётер

Гамильтониан [math]\displaystyle{ H }[/math] известен как генератор эволюции во времени, поскольку он определяет унитарный оператор эволюции во времени [math]\displaystyle{ U(t) = e^{-iHt/\hbar} }[/math] для каждого значения [math]\displaystyle{ t }[/math]. Из этого соотношения между [math]\displaystyle{ U(t) }[/math] и [math]\displaystyle{ H }[/math] следует, что любая наблюдаемая [math]\displaystyle{ A }[/math], которая коммутирует с [math]\displaystyle{ H }[/math] будет сохраняться, поскольку его ожидаемое значение не изменяется с течением времени. Это утверждение обобщается таким образом: любой эрмитов оператор [math]\displaystyle{ A }[/math] может порождать семейство унитарных операторов, параметризованных переменной [math]\displaystyle{ t }[/math]. Под эволюцией, порождённой [math]\displaystyle{ A }[/math], здесь понимается, что любая наблюдаемая [math]\displaystyle{ B }[/math], которая коммутирует с [math]\displaystyle{ A }[/math] будет сохраняться. Более того, если [math]\displaystyle{ B }[/math] сохраняется при эволюции порождённой [math]\displaystyle{ A }[/math], тогда [math]\displaystyle{ A }[/math] сохраняется при эволюции, порождённой [math]\displaystyle{ B }[/math]. Это подразумевает квантовую версию результата, доказанного Эмми Нётер в классической (лагранжевой) механике: для каждого непрерывного преобразования симметрии, оставляющего действие инвариантным имеется соответствующий закон сохранения.

Примеры

Свободная частица

Основная статья: Свободная частица

Плотность вероятности гауссового волнового пакета в координатном пространстве, движущегося в одном измерении в свободном пространстве.

Простейшим примером квантовой системы с координатной степенью свободы является свободная частица в одном пространственном измерении. Свободная частица — это частица, не подверженная внешним воздействиям, поэтому её гамильтониан состоит только из её кинетической энергии, а уравнение Шрёдингера принимает вид:

[math]\displaystyle{ \frac{\hbar}{i}\frac{\partial\psi}{\partial t} = - \frac {\hbar ^2}{2m} \frac {\partial^2\psi}{\partial x^2}\,, }[/math]

где [math]\displaystyle{ i }[/math] — мнимая единица, [math]\displaystyle{ \hbar }[/math] — редуцированная постоянная Планка, [math]\displaystyle{ m }[/math] — масса частицы. Это уравнение допускает разделение переменных, и общее решение уравнения Шрёдингера даётся выражением в виде любого сходящегося интеграла, который описывает волновой пакет плоских волн общего вида

[math]\displaystyle{ \psi (x,t)=\int_{-\infty}^{+\infty}C(k)e^{i(kx-\omega t)}dk\,, }[/math]

где [math]\displaystyle{ \omega }[/math] — частота, [math]\displaystyle{ k }[/math] — волновое число и условие конечности интеграла: [math]\displaystyle{ \lim_{|k|\rightarrow\infty}C(k)\approx |k|^{-\alpha} }[/math] при [math]\displaystyle{ \alpha \geq 1 }[/math]. В частном случае гауссова пакета волновая функция для частицы с волновым числом [math]\displaystyle{ k_0 }[/math] в момент времени [math]\displaystyle{ t=0 }[/math] представляется в виде

[math]\displaystyle{ \psi (x,0)=A\exp\left(-\frac{x^2}{2a^2}+ik_0x\right)\,, }[/math]

где [math]\displaystyle{ a }[/math] — размер волнового пакета, [math]\displaystyle{ A }[/math] — нормировочный множитель. Для такой частицы скорость задаётся выражением [math]\displaystyle{ v_0=\hbar k_0/m\,. }[/math] Это выражение можно разложить по плоским волнам, чтобы найти коэффициент [math]\displaystyle{ C(k)\,, }[/math] который выражается в явном виде

[math]\displaystyle{ C(k) (k)=\frac{Aa}{\sqrt{2\pi}}\exp\left[-\frac{1}{2}(k-k_0)\right]\,. }[/math]

Чтобы найти поведение волновой функции в любой момент времени достаточно проинтегрировать. Плотность задаётся квадратом модуля волновой функции. Она равна в любой момент времени

[math]\displaystyle{ \rho(x,t)=|\psi(x,t)|^2=\frac{|A|^2}{\sqrt{1+\left(\frac{\hbar t}{ma^2}\right)^2}}\exp\left[-\frac{\left(x-\frac{\hbar k_0}{m}t\right)}{a^2\left[1+\left(\frac{\hbar t}{ma^2}\right)^2\right]}\right]\,. }[/math]

Центр гауссового волнового пакета движется в пространстве с постоянной скоростью [math]\displaystyle{ \hbar k_0/m }[/math], как классическая частица, на которую не действуют никакие силы. Однако с течением времени волновой пакет также будет расплываться на величину [math]\displaystyle{ \hbar t/ma }[/math], то есть положение становится всё более и более неопределённым как показано на анимации.

Частица в ящике

Основная статья: Квантовая яма с бесконечными стенками

Одномерный ящик потенциальной энергии (или бесконечная потенциальная яма)

Частица в одномерном потенциале с бесконечными стенками является математически наиболее простым примером, где ограничения приводят к квантованию энергетических уровней. Ящик определяется как имеющая нулевую потенциальную энергию везде внутри определённой области и, следовательно, бесконечную потенциальную энергию повсюду за пределами этой области. Для одномерного случая в [math]\displaystyle{ x }[/math] направлении, независимое от времени уравнение Шрёдингера можно записать в виде

[math]\displaystyle{ - \frac {\hbar ^2}{2m} \frac {d ^2 \psi}{dx^2} = E \psi\,. }[/math]

С дифференциальным оператором, определённым как

[math]\displaystyle{ \hat{p}_x = -i\hbar\frac{d}{dx} }[/math]

предыдущее уравнение напоминает классический аналог кинетической энергии,

[math]\displaystyle{ \frac{1}{2m} \hat{p}_x^2 = E\,, }[/math]

с состоянием [math]\displaystyle{ \psi }[/math] в этом случае с энергией [math]\displaystyle{ E }[/math] совпадает с кинетической энергией частицы.

Общие решения уравнения Шредингера для частицы в ящике таковы:

[math]\displaystyle{ \psi(x) = A e^{ikx} + B e ^{-ikx} \qquad\qquad E = \frac{\hbar^2 k^2}{2m} }[/math]

или, по формуле Эйлера,

[math]\displaystyle{ \psi(x) = C \sin(kx) + D \cos(kx)\,. }[/math]

Бесконечные потенциальные стенки ящика определяют значения неопределённых коэффициентов [math]\displaystyle{ C, D, }[/math] и [math]\displaystyle{ k }[/math] в [math]\displaystyle{ x=0 }[/math] и [math]\displaystyle{ x=L }[/math], где [math]\displaystyle{ \psi }[/math] должна быть равна нулю. Таким образом, при [math]\displaystyle{ x=0 }[/math],

[math]\displaystyle{ \psi(0) = 0 = C\sin(0) + D\cos(0) = D }[/math]

и [math]\displaystyle{ D=0 }[/math]. В [math]\displaystyle{ x=L }[/math],

[math]\displaystyle{ \psi(L) = 0 = C\sin(kL)\,, }[/math]

в котором [math]\displaystyle{ C }[/math] не может быть равно нулю, так как это противоречило бы постулату о том, что [math]\displaystyle{ \psi }[/math] имеет норму равную 1. Следовательно, поскольку [math]\displaystyle{ \sin(kL)=0 }[/math], [math]\displaystyle{ kL }[/math] должно быть целым числом, кратным [math]\displaystyle{ \pi }[/math] , то есть

[math]\displaystyle{ k_n = \frac{n\pi}{L}\qquad\qquad n=1,2,3,\ldots\,. }[/math]

Это ограничение на [math]\displaystyle{ k }[/math] подразумевает ограничение на уровни энергии, что даёт

[math]\displaystyle{ E_n = \frac{\hbar^2 \pi^2 n^2}{2mL^2} = \frac{n^2h^2}{8mL^2}\,. }[/math]

Прямоугольная квантовая яма — это обобщение задачи с бесконечной потенциальной ямой на потенциальные ямы конечной глубины. Проблема конечной потенциальной ямы математически более сложна, чем задача о частице в ящике, поскольку волновая функция не привязана к нулю на стенках ямы. Вместо этого волновая функция должна удовлетворять более сложным граничным условиям, поскольку она отлична от нуля в областях вне ямы. Другая родственная проблема связана с прямоугольным потенциальным барьером, который представляет собой модель эффекта квантового туннелирования, играющего важную роль в работе современных технологий, таких как флэш-память и сканирующая туннельная микроскопия.

Гармонический осциллятор

Основная статья: Квантовый гармонический осциллятор

Некоторые траектории гармонического осциллятора, то есть шарика, прикреплённого к пружине, в классической механике (AB) и квантовой механике (CH). В квантовой механике положение шарика представлено волной (называемой волновой функцией), реальная часть которой показана синим цветом, а мнимая — красным. Некоторые траектории (например, C, D, E и F) представляют собой стоячие волны (или «стационарные состояния»). Каждая частота стоячей волны пропорциональна возможному уровню энергии осциллятора. Это «квантование энергии» не происходит в классической физике, где осциллятор может иметь любую энергию.

Потенциал квантового гармонического осциллятора как и в классическом случае определяется выражением

[math]\displaystyle{ V(x)=\frac{1}{2}m\omega^2x^2\,. }[/math]

Эту задачу можно решить либо путём непосредственного решения уравнения Шрёдингера, что не является тривиальной задачей, либо с помощью более элегантного «лестнечного метода», впервые предложенного Полем Дираком. Собственные состояния квантового гармонического осциллятора задаются

[math]\displaystyle{ \psi_n(x) = \sqrt{\frac{1}{2^n\, n!}} \left(\frac{\lambda}{\pi}\right)^{1/4} e^{ - \frac{\lambda x^2}{2}} H_n\left(\sqrt{\lambda} x \right)\,, }[/math]

где [math]\displaystyle{ \lambda=m\omega/\hbar }[/math] и [math]\displaystyle{ n = 0,1,2,\ldots\,, }[/math] H_n — полиномы Эрмита

[math]\displaystyle{ H_n(x)=(-1)^n e^{x^2}\frac{d^n}{dx^n}\left(e^{-x^2}\right), }[/math]

и соответствующие уровни энергии дискретны

[math]\displaystyle{ E_n = \hbar \omega \left(n + {1\over 2}\right)\,. }[/math]

Это ещё один пример, иллюстрирующий дискретизацию энергии для связанных состояний.

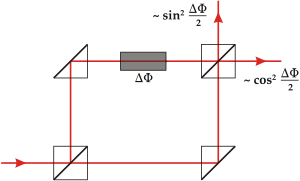
Интерферометр Маха — Цендера

Схема интерферометра Маха — Цендера.

Интерферометр Маха — Цендера (MZI) иллюстрирует концепции суперпозиции и интерференции с линейной алгеброй в дискретном пространстве размерности 2 без использования дифференциальных уравнений. Его можно рассматривать как упрощённую версию эксперимента с двумя щелями, хотя он представляет интерес сам по себе, например, в эксперименте о квантовом ластике с отложенным выбором, эксперименте с бомбами Элицура — Вайдмана и в исследованиях квантовой запутанности.

Если рассмотреть фотон, проходящий через интерферометр, то в каждой точке он может находиться в суперпозиции только двух путей: «нижнего» пути, который начинается слева, проходит прямо через оба светоделителя и заканчивается вверху, и «верхний» путь, который начинается снизу, проходит прямо через оба светоделителя и заканчивается справа. Таким образом, квантовое состояние фотона представляет собой вектор [math]\displaystyle{ \psi \in \mathbb{C}^2 }[/math] — это суперпозиция «нижнего» пути [math]\displaystyle{ \psi_l = \begin{pmatrix} 1 \\ 0 \end{pmatrix} }[/math] и «верхнего» пути [math]\displaystyle{ \psi_u = \begin{pmatrix} 0 \\ 1 \end{pmatrix} }[/math], или, [math]\displaystyle{ \psi = \alpha \psi_l + \beta \psi_u }[/math] для комплексных коэффициентов [math]\displaystyle{ \alpha,\beta }[/math]. Для соблюдения постулата [math]\displaystyle{ \langle \psi,\psi\rangle = 1 }[/math] требуется, чтобы [math]\displaystyle{ |\alpha|^2+|\beta|^2 = 1 }[/math].

Нижний и верхний светоделители задаются матрицами [math]\displaystyle{ B_l = \frac1{\sqrt2}\begin{pmatrix} -1 & 1 \\ 1 & 1 \end{pmatrix} }[/math] и [math]\displaystyle{ B_u = \frac1{\sqrt2}\begin{pmatrix} 1 & -1 \\ 1 & 1 \end{pmatrix} }[/math], что означает, что когда фотон встречает светоделитель, он либо остаётся на том же пути с амплитудой вероятности [math]\displaystyle{ 1/\sqrt{2} }[/math], либо отражается на другой путь с амплитудой вероятности [math]\displaystyle{ 1/\sqrt{2} }[/math] (со сдвигом фазы на π). Зеркало задаётся матрицей [math]\displaystyle{ M = \begin{pmatrix} -1 & 0 \\ 0 & -1 \end{pmatrix}\,. }[/math] Фазовращатель на плече моделируется унитарной матрицей [math]\displaystyle{ P = \begin{pmatrix} e^{i\Delta\Phi} & 0 \\ 0 & 1 \end{pmatrix} }[/math], что означает, что если фотон находится на «верхнем» пути, то он приобретёт относительную фазу [math]\displaystyle{ \Delta\Phi }[/math], или останется неизменным, если он находится на нижнем пути.

Фотон, который входит в интерферометр слева, затем подвергается воздействию светоделителя [math]\displaystyle{ B_l }[/math], зеркала, фазовращателя [math]\displaystyle{ P }[/math] и ещё одного светоделителя [math]\displaystyle{ B_u }[/math], оказывается в состоянии

[math]\displaystyle{ B_uPMB_l\psi_l = \frac{1}{2} \begin{pmatrix} e^{i\Delta\Phi} + 1 \\ e^{i\Delta\Phi} - 1 \end{pmatrix}\,, }[/math]

а вероятности того, что он будет обнаружен справа или вверху, равны соответственно

[math]\displaystyle{ p(u) = |\langle \psi_u, B_uPMB_l\psi_l \rangle|^2 = \cos^2 \frac{\Delta \Phi}{2}\,, }[/math]

[math]\displaystyle{ p(l) = |\langle \psi_l, B_uPMB_l\psi_l \rangle|^2 = \sin^2 \frac{\Delta \Phi}{2}\,. }[/math]

Поэтому можно использовать интерферометр Маха — Цендера для оценки фазового сдвига путём расчёта этих вероятностей.

Можно также определить, что произошло бы, если бы фотон с определённостью находился либо на «нижнем», либо на «верхнем» пути между светоделителями. Этого можно добиться, заблокировав один из путей или, что то же самое, удалив первый светоделитель (и запуская фотон слева или снизу, по желанию). В обоих случаях между путями больше не будет интерференции, и вероятности определяются выражением [math]\displaystyle{ p(u)=p(l) = 1/2 }[/math], независимо от фазы [math]\displaystyle{ \Delta\Phi }[/math]. Из этого можно заключить, что фотон не выбирает тот или иной путь после первого светоделителя, а скорее находится в подлинной квантовой суперпозиции двух путей.

Приложения

Квантовая механика добилась огромных успехов, объяснив многие особенности нашего мира в отношении физических явлений на мелком масштабе, дискретных величин и взаимодействий, которые невозможно объяснить классическими методами. Квантовая механика часто оказывается единственной теорией, которая может раскрыть индивидуальное поведение субатомных частиц, составляющих все формы материи (электроны, протоны, нейтроны, фотоны и другие). Законы физики твёрдого тела и материаловедения находят объяснение в квантовой механике.

Во многих аспектах современные технологии работают в таких масштабах, где существенны квантовые эффекты. Важные приложения квантовой теории включают квантовую химию, квантовую оптику, квантовые вычисления, сверхпроводящие магниты, светоизлучающие диоды, оптические усилители и лазеры, транзисторы и полупроводники, микропроцессоры, медицинскую и исследовательскую визуализацию, такие как магнитно-резонансную томографию и электронную микроскопию. Объяснения многих биологических и физических явлений коренятся в природе химической связи, в первую очередь в макромолекулах ДНК.

По сути, вся современная полупроводниковая электроника построена на квантовой механике, поскольку она опирается на знание зонной структуры твёрдых тел. Технология позволяет легировать различными элементами слои кремния и создавать транзисторы в нанометровом масштабе. Множество таких элементов составляют компьютерные чипы, на которых работают все технологические устройства: настольные компьютеры, ноутбуки, планшеты, смартфоны, бытовая техника и детские игрушки. Источниками света, используемыми для отправки сообщений по оптоволоконным кабелям, во всемирной сети — являются лазеры, созданные при помощи знания о квантовых свойствах материалов. Навигация смартфона обеспечивается Глобальной системой позиционирования, которая функционирует благодаря знанию точного времени. Приёмник GPS в вашем телефоне, чтобы определить ваше расстояние от каждого из спутников с атомными часами на орбите принимает от них сигнал, чтобы вычислить единственную точку вашего местонахождения с точностью до нескольких метров. Оптический переход, используемый для атомных часов, является сверхтонким переходом. На ядерном магнитном резонансе основаны исследования мягких тканей пациента посредством магнитно-резонансной томографии.

Связь с другими научными теориями

Классическая механика

Области применения классической и квантовой механики

Постулаты квантовой механики гласят, что пространство состояний квантовой системы является гильбертовым пространством, и что наблюдаемым системы соответствуют эрмитовые операторы, действующими на векторы в этом пространстве — хотя они не конкретизируют гильбертово пространство и операторы. Их нужно выбирать соответствующим образом, чтобы получить количественное описание квантовой системы, что является необходимым шагом для предсказания поведения физических систем. Для этого пользуются принципом соответствия, эвристикой, которая утверждает, что предсказания квантовой механики сводятся к предсказаниям классической механики в пределе больших квантовых чисел. Можно также начать с установленной классической модели конкретной системы, а затем попытаться угадать лежащую в основе квантовую модель, которая сводится к классической модели в пределе соответствия. Этот подход известен как квантование.

Когда квантовая механика была первоначально сформулирована, она применялась к моделям, пределом соответствия которых была нерелятивистская классическая механика. Например, широко исследованная модель квантового гармонического осциллятора использует явно нерелятивистское выражение для кинетической энергии осциллятора и, таким образом, является квантовой версией классического гармонического осциллятора.

Сложности квантования возникают с хаотическими системами, у которых нет хороших квантовых чисел, и квантовый хаос изучает взаимосвязь между классическими и квантовыми описаниями в этих системах.

Квантовая декогеренция — это механизм, посредством которого квантовые системы теряют когерентность и, таким образом, становятся неспособными демонстрировать многие типично квантовые эффекты: квантовая суперпозиция становится просто суммой вероятностей, а квантовая запутанность — просто классическими корреляциями. Квантовая когерентность обычно не проявляется в макроскопических масштабах, за исключением случая температур, приближающихся к абсолютному нулю, при которых квантовое поведение может проявляться макроскопически.

Многие макроскопические свойства классической системы являются прямым следствием квантового поведения её частей. Например, стабильность объёмного вещества (состоящего из атомов и молекул, которые быстро разрушились бы под действием одних только электрических сил), жёсткость твёрдых тел, а также механические, термические, химические, оптические и магнитные свойства вещества — всё это результат взаимодействия электрических зарядов по законам квантовой механики.

Специальная теория относительности и электродинамика

Ранние попытки объединить квантовую механику со специальной теорией относительности включали замену уравнения Шрёдингера ковариантным уравнением, таким как уравнение Клейна — Гордона или уравнение Дирака. Хотя эти теории были успешными в объяснении многих экспериментальных результатов, они имели некоторые неудовлетворительные свойства, проистекающие из пренебрежения рождением и аннигиляцией частиц. Полностью релятивистская квантовая теория потребовала развития квантовой теории поля, которая использует квантование поля, а не фиксированный набор частиц. Первая согласованная квантовая теория поля — квантовая электродинамика, даёт полное описание электромагнитного взаимодействия. Квантовая электродинамика, наряду с общей теорией относительности, является одной из самых точных когда-либо созданных физических теорий.

Полный аппарат квантовой теории поля часто не нужен для описания электродинамических систем. Более простой подход, который использовался с момента зарождения квантовой механики, состоит в том, чтобы рассматривать заряженные частицы как объекты квантовой механики, на которые воздействует классическое электромагнитное поле. Например, элементарная квантовая модель атома водорода описывает электрическое поле атома водорода с помощью классического [math]\displaystyle{ \textstyle -e^2/(4 \pi\epsilon_{_0}r) }[/math] кулоновского потенциала. Этот «полуклассический» подход терпит неудачу, если квантовые флуктуации электромагнитного поля играют важную роль, например, при излучении фотонов заряженными частицами.

Также были разработаны квантовые теории поля для сильного ядерного взаимодействия и слабого ядерного взаимодействия. Квантовая теория поля сильного ядерного взаимодействия называется квантовой хромодинамикой и описывает взаимодействия субъядерных частиц, таких как кварки и глюоны. Слабое ядерное взаимодействие и электромагнитное взаимодействие были объединены в их квантованных формах в единую квантовую теорию поля (известную как электрослабая теория) физиками Абдусом Саламом, Шелдоном Глэшоу и Стивеном Вайнбергом.

Отношение к общей теории относительности

Несмотря на то, что предсказания как квантовой теории, так и общей теории относительности были подтверждены строгими и повторяющимися эмпирическими данными, их абстрактные формализмы противоречат друг другу, в результате их оказалось чрезвычайно трудно включить в одну непротиворечивую связную модель. Гравитацией можно пренебречь во многих областях физики элементарных частиц, поэтому объединение общей теории относительности и квантовой механики не является насущной проблемой в этих конкретных приложениях. Однако отсутствие правильной теории квантовой гравитации — это важная проблема физической космологии и поиска физиками элегантной «Теории всего». Следовательно, устранение несоответствий между обеими теориями стало главной целью физики 20-го и 21-го веков. Эта теория всего объединит не только модели субатомной физики, но и выведет четыре фундаментальные силы природы из одной силы или явления.

Одним из предложений для этого является теория струн, которая утверждает, что точечные частицы в физике элементарных частиц заменяются одномерными объектами, называемыми струнами. Теория струн описывает, как эти струны распространяются в пространстве и взаимодействуют друг с другом. На масштабах расстояний, превышающих масштаб струны, струна выглядит как обычная частица, а её масса, заряд и другие свойства определяются колебательным состоянием струны. В теории струн одно из многих колебательных состояний струны соответствует гравитону, квантовомеханической частице, переносчика гравитационного взаимодействия.

Другой популярной теорией является петлевая квантовая гравитация, которая описывает квантовые свойства гравитации и, таким образом, является теорией квантового пространства-времени. Петлевая теория гравитации — это попытка объединить и адаптировать стандартную квантовую механику и стандартную общую теорию относительности. Эта теория описывает пространство как чрезвычайно тонкую ткань, «сотканную» из конечных петель, называемых спиновыми сетями. Эволюция спиновой сети во времени называется спиновой пеной. Характерным масштабом длины спиновой пены является планковская длина, приблизительно равная 1,616 × 10⁻³⁵ м, поэтому длины короче планковской длины не имеют физического смысла в петлевой теории гравитации.

Философские последствия

Основная статья: Интерпретация квантовой механики

С момента своего создания многие результаты и нелогичные аспекты квантовой механики вызывали сильные философские споры и возникновение множества интерпретаций. Дискуссии затрагивают вероятностную природу квантовой механики, трудности с коллапсом волновой функции и связанных с этим проблему измерения, а также квантовую нелокальность. Возможно, единственный консенсус, который существует по этим вопросам, заключается в отсутствие консенсуса. Ричард Фейнман однажды сказал: «Думаю, я могу с уверенностью сказать, что никто не понимает квантовую механику». По словам Стивена Вайнберга: «на мой взгляд, в настоящее время нет полностью удовлетворительной интерпретации квантовой механики».

Взгляды Нильса Бора, Вернера Гейзенберга и других физиков на квантовую механику часто объединяют в «копенгагенскую интерпретацию». Согласно этим взглядам, вероятностный характер квантовой механики — это не временное свойство, которое в будущем будет заменено детерминистской теорией, а окончательный отказ от классической идеи «причинности». Бор, в частности, подчёркивал, что любое чётко определённое применение квантовомеханического формализма всегда должно ссылаться на экспериментальную установку из-за взаимодополняющего характера результатов, полученных в различных экспериментальных ситуациях. Интерпретации копенгагенского типа остаются популярными и в 21 веке.

Альберта Эйнштейна, одного из основателей квантовой теории, беспокоило её явное несоблюдение некоторых заветных метафизических принципов, таких как детерминизм и локальность. Давний обмен мнениями между Эйнштейном и Бором о значении и статусе квантовой механики теперь известен как дебаты Бора и Эйнштейна. Эйнштейн считал, что в основе квантовой механики должна лежать теория, явно запрещающая действие на расстоянии. Он утверждал, что квантовая механика была неполной; теория была верной, но не фундаментальной, аналогично тому, как верна термодинамика, но фундаментальной теорией, лежащей в её основе, является статистическая механика. В 1935 году Эйнштейн и его сотрудники Борис Подольский и Натан Розен опубликовали аргумент о том, что принцип локальности подразумевает неполноту квантовой механики. Их мысленный эксперимент, позже назовут парадоксом Эйнштейна — Подольского — Розена (ЭПР). В 1964 году Джон Белл показал, что принцип локальности ЭПР вместе с детерминизмом на самом деле несовместимы с квантовой механикой: они подразумевают ограничения на корреляции, создаваемые системами на расстоянии, теперь известные как неравенства Белла, которые могут нарушаться запутанными частицами. С тех пор было проведено несколько опытов, в которых измерялись эти корреляции, в результате чего оказалось, что неравенства Белла действительно нарушаются и, таким образом, фальсифицируют соединение локальности с детерминизмом.

Бомовская механика показывает, что можно переформулировать квантовую механику, сделав её детерминированной, ценой явной нелокальности. Она приписывает физической системе не только волновую функцию, но и реальное положение, которое детерминистически развивается под нелокальным управляющим уравнением. Эволюция физической системы во все времена задаётся уравнением Шрёдингера вместе с ведущим уравнением; никогда не бывает коллапса волновой функции. Этот подход разрешает проблему измерения.

Многомировая интерпретация Эверетта, сформулированная в 1956 году, утверждает, что все возможности, описываемые квантовой теорией, одновременно возникают в мультивселенной, состоящей в основном из независимых параллельных вселенных. Это исключает проблему коллапса волнового пакета, поскольку все возможные состояния измеряемой системы и измерительного прибора вместе с наблюдателем присутствуют в реальной физической квантовой суперпозиции. В то время как мультивселенная детерминирована, мы воспринимаем недетерминистическое поведение, управляемое вероятностями, потому что мы не наблюдаем мультивселенную в целом, а только одну параллельную вселенную в каждый момент времени. Как именно это должно работать, было предметом многочисленных споров. Было предпринято несколько попыток вывода правила Борна без единого мнения о том, были ли они успешными.

Реляционная квантовая механика появилась в конце 1990-х годов как современная производная от идей копенгагенского типа, а несколько лет спустя была разработана теория квантового байесианства.

Примечания

Комментарии

Источники