Инверсия (геометрия)

Инве́рсия (от лат. inversio «обращение») относительно окружности — преобразование евклидовой плоскости, переводящее обобщённые окружности (окружности либо прямые) в обобщённые окружности, при котором одна из окружностей поточечно переводится в себя.

Определение

Инверсия

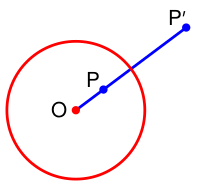
Пусть в евклидовой плоскости задана некоторая окружность [math]\displaystyle{ \Gamma }[/math] с центром [math]\displaystyle{ O }[/math] (называемым полюсом инверсии, или центром инверсии, эта точка выколота) и радиусом [math]\displaystyle{ R }[/math]. Инверсия точки [math]\displaystyle{ P }[/math] относительно [math]\displaystyle{ \Gamma }[/math] есть точка [math]\displaystyle{ P' }[/math], лежащая на луче [math]\displaystyle{ OP }[/math] такая, что

[math]\displaystyle{ |OP'|\cdot|OP|=R^2. }[/math]

Инверсия переводит внутреннюю область окружности во внешнюю и обратно.

Часто к плоскости добавляют «бесконечно удалённую точку» [math]\displaystyle{ \infty }[/math] и считают её инверсным образом [math]\displaystyle{ O }[/math], а [math]\displaystyle{ O }[/math] — инверсным образом [math]\displaystyle{ \infty }[/math]. В этом случае инверсия является биективным преобразованием этой расширенной «круговой плоскости».

Аналогично определяется инверсия евклидова пространства относительно сферы и инверсия в евклидовых пространствах более высоких размерностей.

Свойства

Образ центра окружности не является центром образа

Инверсия относительно окружности [math]\displaystyle{ \Gamma }[/math] с центром O обладает следующими основными свойствами:

Инверсия является инволюцией: если точка P переходит в точку Q, то и точка Q переходит в точку P.
Прямая, проходящая через O, переходит в себя.
Прямая, не проходящая через O, переходит в окружность, проходящую через O с выколотой точкой O; и обратно, окружность, проходящая через O, переходит в прямую, не проходящую через O.
Окружность, не проходящая через O, переходит в окружность, не проходящую через O (при этом образ её центра не является центром образа).
Инверсия является конформным отображением второго рода (т. е. она сохраняет углы между кривыми и меняет ориентацию).

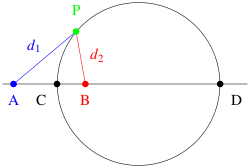
[math]\displaystyle{ d_1/d_2 = \text{const} }[/math]

Инверсия относительно окружности Аполлония, определяемой равенством [math]\displaystyle{ k = \tfrac{PA}{PB} }[/math], меняет местами точки [math]\displaystyle{ A }[/math] и [math]\displaystyle{ B }[/math].
Окружность или прямая, перпендикулярная к [math]\displaystyle{ \Gamma }[/math], переходит в себя.

Замечание

В теории окружностей и инверсии две окружности, пересекающиеся под прямым углом, называются ортогональными (перпендикулярными). Окружности можно считать ортогональными, если они образуют прямой угол друг с другом. Обычно угол между кривыми — это угол между их касательными, проведёнными в точке их пересечения.
В теории окружностей и инверсии прямая перпендикулярна к окружности [math]\displaystyle{ \Gamma }[/math], если она проходит через центр последней.

Построение

Построение образа точки при инверсии относительно окружности

Получить образ P' точки P при инверсии относительно данной окружности с центром O можно следующим образом^[1]:

Если расстояние от P до O больше радиуса окружности — провести из P касательную к окружности, тогда перпендикуляр к прямой OP из точки касания пересечёт эту прямую в искомой точке P'.
Если расстояние от P до O меньше радиуса окружности — провести через P перпендикуляр к OP, а через точку его пересечения с окружностью — касательную к ней, которая пересечёт OP в искомой точке P'.
Если расстояние от P до O равно радиусу окружности, образ P совпадёт с ней самой.

Координатные представления

Декартовы координаты

Инверсия относительно единичной окружности с центром в начале координат задаётся соотношением

[math]\displaystyle{ (x,y)\mapsto \left(\frac{x}{x^2+y^2},\frac{y}{x^2+y^2}\right) }[/math].

Если точку плоскости задать одной комплексной координатой [math]\displaystyle{ z=x+iy }[/math], то это выражение можно представить в виде

[math]\displaystyle{ z\mapsto (\bar z)^{-1} }[/math],

где [math]\displaystyle{ \bar z }[/math] — комплексно сопряжённое число для [math]\displaystyle{ z }[/math]. Данная функция комплексного переменного является антиголоморфной, откуда, в частности, следует конформность инверсии.

В общем случае инверсия относительно окружности с центром в точке [math]\displaystyle{ O=(x_0,y_0) }[/math] и радиусом [math]\displaystyle{ r }[/math] задаётся соотношением

[math]\displaystyle{ (x,y)\mapsto \left(x_0+\frac{r^2(x-x_0)}{(x-x_0)^2+(y-y_0)^2},y_0+\frac{r^2(y-y_0)}{(x-x_0)^2+(y-y_0)^2}\right) }[/math].

Полярные координаты

Инверсия относительно окружности радиуса [math]\displaystyle{ r }[/math] с центром в начале координат задаётся соотношением

[math]\displaystyle{ (\phi,\rho)\mapsto (\phi,r^2/\rho) }[/math].

Приложения

Применением инверсии решаются
- задача Аполлония,
- тождество Птолемея.

На свойствах инверсии основан механизм Липкина — Посселье.

Применением инверсии доказывается теорема Мора — Маскерони, которая утверждает, что все построения, которые можно сделать с помощью циркуля и линейки, можно сделать с помощью одного циркуля (прямая считается построенной, если известны две её точки)^[2]^[3]

Существует доказательство свойств окружности Аполлония, основанное на свойстве инверсии.^[4]

При помощи инверсии доказывается поризм Штейнера: в доказательстве используется тот факт, что для любых непересекающихся окружностей существует инверсия, превращающая их в концентрические.

При помощи инверсии доказывается то, что равны две архимедовы окружности-близнецы в арбелосе.^[2]

При помощи инверсии доказываются свойства окружностей в поризме Паппа Александрийского.^[2]

При помощи инверсии доказывается Теорема о бабочке.^[2]

Вариации и обобщения

Инверсия относительно конического сечения

Можно определить инверсию относительно произвольного невырожденного конического сечения, с той лишь разницей, что величина [math]\displaystyle{ R }[/math] будет (переменным) расстоянием от центра [math]\displaystyle{ O }[/math] соответствующей кривой (в случае эллипса и гиперболы) до точек пересечения этой кривой с прямой [math]\displaystyle{ OP }[/math].

В случае инверсии относительно гиперболы, в зависимости от сектора, в котором находится точка [math]\displaystyle{ P }[/math] между асимптотами, возможен случай, когда прямая [math]\displaystyle{ OP }[/math] не пересекается с гиперболой. Тогда для вычисления [math]\displaystyle{ R }[/math] берётся точка пересечения этой прямой с сопряжённой гиперболой (если только точка [math]\displaystyle{ P }[/math] не лежит на асимптоте), а соответствующая величина [math]\displaystyle{ R^2 }[/math] берётся со знаком минус, то есть луч [math]\displaystyle{ OP' }[/math] направляется в сторону, противоположную лучу [math]\displaystyle{ OP }[/math].

Инверсия относительно параболы — это просто симметричное отражение относительно неё вдоль прямой, параллельной оси параболы.

Альтернативное определение — инверсия относительно конического сечения [math]\displaystyle{ \mathcal K }[/math] как середина хорды, высекаемой полярой точки [math]\displaystyle{ P }[/math] относительно [math]\displaystyle{ \mathcal K }[/math] на [math]\displaystyle{ \mathcal K }[/math]. Однако в случае, когда соответствующая поляра не пересекает [math]\displaystyle{ \mathcal K }[/math], для полноты определения приходится применять это, частичное, определение в обратную сторону (то есть [math]\displaystyle{ P' }[/math] — это такая точка, что [math]\displaystyle{ P }[/math] является серединой хорды, высекаемой полярой [math]\displaystyle{ P' }[/math] на [math]\displaystyle{ \mathcal K }[/math]), что не всегда удобно.

См. также

Примечания

↑ Погорелов А. В. Геометрия. — М.: Наука, 1983. — С. 41—42. — 288 с.
↑ ^2,0 ^2,1 ^2,2 ^2,3 Жижилкин, 2009.
↑ Курант, 2000.
↑ § 124 «Геометрии» А. Ю. Давидова.

Ссылки

Ануфриенко С. А. Симметрия относительно окружности.
Бакельман И. Я. Инверсия. Популярные лекции по математике, Вып. 44, М., Наука, 1966.
Жижилкин И. Д. Инверсия.. — М.: МЦНМО, 2009.
Курант Р., Роббинс Г. Что такое математика?. — М.: МЦМО, 2000. — С. Гл. III, § 4.. — ISBN 5–900916–45–6.

[1] Погорелов А. В. Геометрия. — М.: Наука, 1983. — С. 41—42. — 288 с.

[_11de5b5a5f8052ca-2] 2,0 ^2,1 ^2,2 ^2,3 Жижилкин, 2009.

[_8d24b58b602ac5c0-3] Курант, 2000.

[4] § 124 «Геометрии» А. Ю. Давидова.

[1]

[2]

[3]

[4]