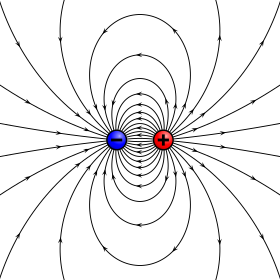
Диполь (электродинамика)

Дипо́ль (фр. dipôle, от греч. di(s) «дважды» + polos «ось», «полюс», буквально — «дву(х)полюсность») — идеализированная система, служащая для приближённого описания поля, создаваемого более сложными системами зарядов, а также для приближенного описания действия внешнего слоя поля на такие системы.

Магнитное поле Земли примерно совпадает с полем диполя. Однако «N» и «S» (северный и южный) полюса отмечены «географически», то есть противоположно принятому обозначению для полюсов магнитного диполя.

Типичный и стандартный пример диполя — два заряда, равные по величине и противоположные по знаку, находящиеся друг от друга на расстоянии, очень малом по сравнению с расстоянием до точки наблюдения. Поле такой системы полностью описывается дипольным приближением при стремлении расстояния между зарядами к нулю при сохранении произведения величины заряда на расстояние между зарядами — постоянным (или стремящимся к конечному пределу; эта константа или этот предел будет дипольным моментом такой системы).

Эквипотенциальные поверхности электрического диполя

Силовые линии электрического диполя

Дипольное приближение, выполнение которого обычно подразумевается, когда говорится о поле диполя, основано на разложении потенциалов поля в ряд по степеням радиус-вектора, характеризующего положение зарядов-источников, и отбрасывании всех членов выше первого порядка.
Полученные функции будут эффективно описывать поле в случае, если:

1. размеры создающей или излучающей поле системы (области, содержащей заряды) малы по сравнению с рассматриваемыми расстояниями, так что отношение характерного размера системы к длине радиус-вектора является малой величиной и имеет смысл рассмотрение лишь первых членов разложения потенциалов в ряд;
2. член первого порядка в разложении не равен 0, в противном случае нужно использовать приближение более высокой мультипольности;
3. в уравнениях рассматриваются градиенты потенциалов не выше первого порядка.

Дипольный момент системы

Электрический диполь

Электрический диполь — идеализированная электронейтральная система, состоящая из точечных и равных по абсолютной величине положительного и отрицательного электрических зарядов.

Другими словами, электрический диполь представляет собой совокупность двух равных по абсолютной величине разноимённых точечных зарядов, находящихся на некотором расстоянии друг от друга.

Произведение вектора [math]\displaystyle{ \vec l, }[/math] проведённого от отрицательного заряда к положительному, на абсолютную величину зарядов [math]\displaystyle{ q\,, }[/math] называется дипольным моментом: [math]\displaystyle{ \vec d=q\vec l. }[/math]

Во внешнем электрическом поле [math]\displaystyle{ \vec E }[/math] на электрический диполь действует момент сил [math]\displaystyle{ {\vec d}\times{\vec E}, }[/math] который стремится повернуть его так, чтобы дипольный момент развернулся вдоль направления поля.

Потенциальная энергия электрического диполя в (постоянном) электрическом поле равна [math]\displaystyle{ -{\vec E}\cdot{\vec d}. }[/math] (В случае неоднородного поля это означает зависимость не только от момента диполя — его величины и направления, но и от места, точки нахождения диполя).

Вдали от электрического диполя напряжённость его электрического поля убывает с расстоянием [math]\displaystyle{ R }[/math] как [math]\displaystyle{ R^{-3}, }[/math] то есть быстрее, чем у точечного заряда ([math]\displaystyle{ E \sim R^{-2} }[/math]).

Дипольное приближение для электростатического поля нейтральной системы

Любая в целом электронейтральная система, содержащая электрические заряды, в некотором приближении (то есть собственно в дипольном приближении) может рассматриваться как электрический диполь с моментом [math]\displaystyle{ \vec d = \sum_i q_i {\vec r}_i, }[/math] где [math]\displaystyle{ q_i }[/math] — заряд [math]\displaystyle{ i }[/math]-го элемента, [math]\displaystyle{ {\vec r}_i }[/math] — его радиус-вектор. При этом дипольное приближение будет корректным, если расстояние, на котором изучается электрическое поле системы, велико по сравнению с её характерными размерами.

В точечном приближении, поле, создаваемое диполем в точке с радиус-вектором [math]\displaystyle{ {\vec r} }[/math] даётся следующим соотношением:

[math]\displaystyle{ \vec {E} = \frac{1}{4\pi \varepsilon_0}\frac{3 \vec {r} (\vec{r}, \vec{d})-{r^2} \vec{d}}{r^5} }[/math]

Дипольное приближение для электростатического поля не-нейтральной системы

Не электрически нейтральная система очевидным образом может быть представлена как сумма (суперпозиция) электрически нейтральной системы и точечного заряда. Для этого достаточно поместить куда-то внутрь системы точечный заряд, противоположный ее суммарному заряду, и в ту же точку еще один точечный заряд, равный ее суммарному заряду. После чего рассматривать первый заряд вместе с остальной системой (ее дипольный момент будет очевидно равен дипольному моменту, вычисленному по формуле, приведенной выше, если за начало координат взять положение добавленного точечного заряда: тогда сам добавленный заряд не войдет в выражение). Второй же точечный заряд даст кулоновское поле.

То есть, вдалеке от такой системы электростатическое поле, создаваемое ею, в дипольном приближении будет суммой (суперпозицией) кулоновского поля, создаваемого зарядом этой системы [math]\displaystyle{ Q = \sum_i q_i, }[/math] условно помещенного в некоторую точку внутри системы зарядов, и поля диполя с моментом [math]\displaystyle{ \vec d = \sum_i q_i {\vec r}_i, }[/math], где радиус-векторы берутся от положения заряда [math]\displaystyle{ Q. }[/math] Нетрудно показать при этом и что такое поле в дипольном приближении не зависит от произвольно (но обязательно внутри системы зарядов или очень близко к ней) выбранного положения точечного заряда [math]\displaystyle{ Q, }[/math] поскольку поправка в нужном порядке будет компенсироваться изменением вычисленного дипольного момента (ведь перемещение положения заряда [math]\displaystyle{ Q }[/math] на некоторое [math]\displaystyle{ \vec D }[/math] эквивалентно наложению диполя с моментом [math]\displaystyle{ Q \vec D }[/math]).

Магнитный диполь

Магнитный диполь — аналог электрического, который можно представить себе как систему двух «магнитных зарядов» — магнитных монополей. Эта аналогия условна, так как магнитные заряды не обнаружены. В качестве модели магнитного диполя можно рассматривать небольшую (по сравнению с расстояниями, на которых излучается генерируемое диполем магнитное поле) плоскую замкнутую проводящую рамку площади [math]\displaystyle{ S\,, }[/math] по которой течёт ток [math]\displaystyle{ I\,. }[/math] При этом магнитным моментом диполя (в системе СГСМ) называют величину [math]\displaystyle{ {\vec \mu} = I S {\vec n}, }[/math] где [math]\displaystyle{ {\vec n} }[/math] — единичный вектор, направленный перпендикулярно плоскости рамки в том направлении, при наблюдении в котором ток в рамке представляется текущим по часовой стрелке.

Выражения для вращающего момента [math]\displaystyle{ \vec M }[/math], действующего со стороны магнитного поля на магнитный диполь, и потенциальной энергии постоянного магнитного [math]\displaystyle{ U }[/math]диполя в магнитном поле, аналогичны соответствующим формулам для взаимодействия электрического диполя с электрическим полем, только входят туда магнитный момент [math]\displaystyle{ \vec m }[/math] и вектор магнитной индукции [math]\displaystyle{ \vec B }[/math]:

[math]\displaystyle{ \vec M = \vec m \times \vec B, }[/math]

[math]\displaystyle{ U = - \vec m \cdot \vec B. }[/math]

Поле колеблющегося диполя

В этом разделе рассматривается поле, создаваемое точечным электрическим диполем [math]\displaystyle{ \mathbf{d}(t), }[/math] находящимся в заданной точке пространства.

Поле на близких расстояниях (ближняя зона)

Поле точечного диполя, колеблющегося в вакууме, имеет вид

[math]\displaystyle{ \mathbf{E} = \frac{3 \mathbf{n} (\mathbf{n}, \mathbf{d})-\mathbf{d}}{R^3} + \frac{3 \mathbf{n} (\mathbf{n}, \dot{\mathbf{d}}) - \dot{\mathbf{d}}}{c R^2} + \frac{ \mathbf{n} (\mathbf{n}, \ddot{\mathbf{d}}) - \ddot{\mathbf{d}}}{c^2 R} }[/math]

[math]\displaystyle{ \mathbf{B} = \left[\frac{\dot{\mathbf{d}}}{c R^2} + \frac{\ddot{\mathbf{d}}}{R c^2} , \mathbf{n} \right] = \left[\mathbf{n} , \mathbf{E} + \frac{\mathbf{d}}{R^3}\right], }[/math]

где [math]\displaystyle{ \mathbf{n} = \frac{\mathbf{R}}{R} }[/math] — единичный вектор в рассматриваемом направлении, [math]\displaystyle{ c }[/math] — скорость света.

Этим выражениям можно придать несколько другую форму, если ввести вектор Герца

[math]\displaystyle{ \mathbf{Z} = - \frac{1}{R} \cdot \mathbf{d}\left(t-\frac{R}{c}\right). }[/math]

Напомним, что диполь покоится в начале координат, так что [math]\displaystyle{ \mathbf{d} }[/math] является функцией одной переменной. Тогда

[math]\displaystyle{ \mathbf{E} = - \operatorname{rot}\,\operatorname{rot}\,\mathbf{Z}, }[/math]

[math]\displaystyle{ \mathbf{B} = - \frac{1}{c}\operatorname{rot}\,\dot{\mathbf{Z}}. }[/math]

При этом потенциалы поля можно выбрать в виде

[math]\displaystyle{ \mathbf{A} = - \frac{\dot{\mathbf{Z}}}{c}, ~~ \phi = \operatorname{div}\,\mathbf{Z}. }[/math]

Указанные формулы можно применять всегда, когда применимо дипольное приближение.

Дипольное излучение (излучение в волновой зоне или дальней зоне)

Приведённые формулы существенно упрощаются, если размеры системы много меньше длины излучаемой волны, то есть скорости зарядов много меньше c, а поле рассматривается на расстояниях много больших, чем длина волны. Такую область поля называют волновой зоной. Распространяющуюся волну можно в этой области считать практически плоской. Из всех членов в выражениях для [math]\displaystyle{ \mathbf{E} }[/math] и [math]\displaystyle{ \mathbf{B} }[/math] существенными оказываются только члены, содержащие вторые производные от [math]\displaystyle{ \mathbf{d}, }[/math] так как

[math]\displaystyle{ \frac{\dot{\mathbf{d}}}{c} \approx \frac{d}{\lambda}, }[/math]

[math]\displaystyle{ \frac{\ddot{\mathbf{d}}}{c^2} \approx \frac{d}{\lambda^2}. }[/math]

Выражения для полей в системе СГС принимают вид

[math]\displaystyle{ \mathbf{H} = \frac{1}{c^2 R}[\ddot{\mathbf{d}},\mathbf{n}], ~~ \mathbf{H} = [\mathbf{n} , \mathbf{E}], }[/math]

[math]\displaystyle{ \mathbf{E} = \frac{1}{c^2 R}\left[ [\ddot{\mathbf{d}},\mathbf{n}] , \mathbf{n} \right], ~~ \mathbf{E} = [\mathbf{B} , \mathbf{n}]. }[/math]

В плоской волне интенсивность излучения в телесный угол [math]\displaystyle{ d\Omega }[/math] равна

[math]\displaystyle{ dI = c \frac{H^2}{4\pi}R^2 d\Omega, }[/math]

поэтому для дипольного излучения

[math]\displaystyle{ dI = \frac{1}{4 \pi c^3}[\ddot{\mathbf{d}}, \mathbf{n}]^2 d\Omega = \frac{\ddot{\mathbf{d}}^2}{4\pi c^3}\sin^2{\theta} d\Omega. }[/math]

где [math]\displaystyle{ \theta }[/math] — угол между векторами [math]\displaystyle{ \ddot{\mathbf{d}} }[/math] и [math]\displaystyle{ \mathbf{n}. }[/math] Найдём полную излучаемую энергию. Учитывая, что [math]\displaystyle{ d\Omega = 2\pi\, \sin{\theta}\, d\theta, }[/math] проинтегрируем выражение по [math]\displaystyle{ d\theta }[/math] от [math]\displaystyle{ 0 }[/math] до [math]\displaystyle{ \pi. }[/math] Полное излучение равно

[math]\displaystyle{ I = \frac{2}{3 c^3} {\ddot{\mathbf{d}}}^2. }[/math]

Укажем спектральный состав излучения. Он получается заменой вектора [math]\displaystyle{ \ddot{\mathbf{d}} }[/math] на его Фурье-компоненту и одновременным умножением выражения на 2. Таким образом,

[math]\displaystyle{ d \mathcal{E}_\omega = \frac{4 \omega^4}{3 c^3} \left| \mathbf{d}_\omega \right|^2 \frac{d\omega}{2\pi}. }[/math]

См. также

• Мультиполь
• Квадруполь
• Октуполь
• Дипольный момент
• Магнитный дипольный момент
• Диполярная система координат

Литература

• Ландау Л. Д., Лифшиц Е. М. Теория поля. — Издание 7-е, исправленное. — М.: Наука, 1988. — 512 с. — («Теоретическая физика», том II). — ISBN 5-02-014420-7.
• Ахманов С. А., Никитин С. Ю., «Физическая оптика», 2004.