График функции

Пример графика функции [math]\displaystyle{ x^3 }[/math] в прямоугольных координатах

Пример графика диаграммы направленности дипольного излучателя в полярных координатах

Изометрический график двумерной поверхности функции двух переменных [math]\displaystyle{ f(x,y) = \sin\left(x^2\right)\cos\left(y^2\right) }[/math]

Гра́фик фу́нкции — геометрическое понятие в математике, дающее представление о геометрическом образе функции.

Наиболее наглядны графики вещественнозначных функций вещественного переменного одной переменной.

Для непрерывной функции двух переменных [math]\displaystyle{ z = f(x,\ y) }[/math] их графики представляют собой поверхности в трёхмерном пространстве, являющиеся геометрическим местом точек [math]\displaystyle{ z,\ x,\ y. }[/math] Эти поверхности могут быть изображены на плоскости в какой-либо изометрической проекции (см. рисунок).

Обычно графики строят в прямоугольной системе координат, на плоскости эту систему координат называют декартовой системой координат. Также графики для повышения наглядности часто строят в других системах координат, например, в полярной системе координат или других косоугольных системах координат.

В случае использования прямоугольной системы координат, график функции — это геометрическое место точек плоскости, абсциссы (x) и ординаты (y), которые связаны отображаемой функцией:

точка [math]\displaystyle{ (x,y) }[/math] располагается (или находится) на графике функции [math]\displaystyle{ y=f(x) }[/math] тогда и только тогда, когда [math]\displaystyle{ y=f(x) }[/math].

Таким образом, функция может быть адекватно описана своим графиком.

Из определения графика функции следует, что далеко не всякое множество точек плоскости может быть графиком некоторой функции, например, из требования однозначности функции вытекает, что никакая прямая, параллельная оси ординат не может пересекать график функции более чем в одной точке. Если функция обратима, то график обратной функции (как подмножество плоскости) будет совпадать с графиком самой функции (это, попросту, одно и то же подмножество плоскости).

Некоторые функции определены только в конечном дискретном множестве аргумента, при этом график таких функций представляет собой множество точек, например график функции определённой как:

[math]\displaystyle{ f(x)=\left\{\begin{matrix} a, & x=1 \\ b, & x=2 \\ c, & x=3 \end{matrix}\right. }[/math]

представляет собой множество из трёх точек [math]\displaystyle{ (1,\ a); ~ (2,\ b); ~ (3,\ c). }[/math]

График гладкой (требуемое количество раз дифференцируемой функции) является плоской кривой той же степени гладкости.

Некоторые графики имеют самостоятельные имена, например:

График линейной функции — прямая.
График квадратной функции — парабола.
График дробной функции — гипербола.
График показательной функции — экспонента
График синуса — синусоида, график косинуса — косинусоида, тангенса — тангенсоида и т. д.

Определение графика

При рассмотрении отображения произвольного вида [math]\displaystyle{ f:X\to Y }[/math], действующего из множества [math]\displaystyle{ X }[/math] в множество [math]\displaystyle{ Y }[/math], графиком функции называется следующее множество упорядоченных пар:

[math]\displaystyle{ \Gamma_f=\{\,(x,f(x))\in X\times Y\mid x\in X\,\}. }[/math]

В частности, при рассмотрении динамических систем, изображающая точка [math]\displaystyle{ (t,f(t)) }[/math] представляет собою график решения соответствующего дифференциального уравнения с заданными начальными условиями такой график часто называют фазовой траекторией системы.

Примеры

Функция	График функции	Описание
[math]\displaystyle{ f(x) = \begin{cases} -1, & x\lt 0 \\ 0, & x=0 \\ 1, & x\gt 0 \end{cases} }[/math]		Функция [math]\displaystyle{ y=\sgn(x). }[/math] В точке [math]\displaystyle{ x=0 ~ ~ y=0. }[/math]
[math]\displaystyle{ f(x) = \begin{cases} 0, & x=1 \\ 8, & x=2 \\ 15, & x=3 \end{cases} }[/math]		Пример графика функции, определённой только в трёх точках [math]\displaystyle{ \{1,2,3\} }[/math] и содержит только три точки с координатами [math]\displaystyle{ (1,0) }[/math], [math]\displaystyle{ (2,8) }[/math] и [math]\displaystyle{ (3,15). }[/math]
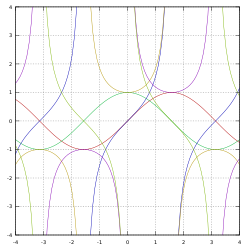
[math]\displaystyle{ f(x)=\sin(x) }[/math] [math]\displaystyle{ f(x)=\cos(x) }[/math] [math]\displaystyle{ f(x)=\operatorname{tg}(x) }[/math] [math]\displaystyle{ f(x)=\operatorname{ctg}(x) }[/math] [math]\displaystyle{ f(x)=\sec(x) }[/math] [math]\displaystyle{ f(x)=\operatorname{cosec}(x) }[/math]		Графики тригонометрических функций: синуса, косинуса, тангенса, котангенса, секанса, косеканса
[math]\displaystyle{ f(x)=\frac{1}{x} }[/math]		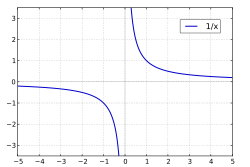График гиперболы. При [math]\displaystyle{ x=0 }[/math] претерпевает разрыв 2-го рода и в точке [math]\displaystyle{ x=0 }[/math] не определена.
[math]\displaystyle{ f(x)=b^x }[/math]		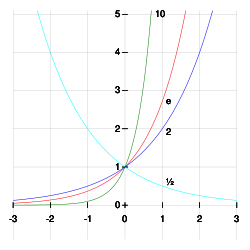Графики функций [math]\displaystyle{ y=b^x }[/math] различными основаниями [math]\displaystyle{ b }[/math]: основание: 10 основание: e основание: 2 основание: 12 Каждая кривая проходит через точку (0, 1).
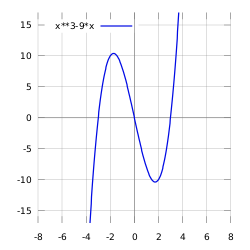
[math]\displaystyle{ f(x)=x^3-9x }[/math]		График [math]\displaystyle{ f(x)=x^3-9x }[/math] кубического многочлена вещественной переменной, это множество [math]\displaystyle{ \{(x, x^3-9 x)\in \R^2\ \| x\in\R\} }[/math].