Биномиальное распределение
| Биномиальное распределение | |
|---|---|
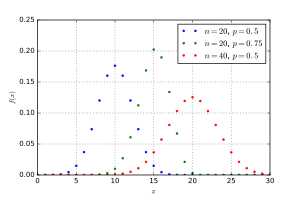 Функция вероятности Функция вероятности | |
 Функция распределения Функция распределения | |
| Обозначение | [math]\displaystyle{ B(n,p) }[/math] |
| Параметры |
[math]\displaystyle{ n \geqslant 0 }[/math] — число «испытаний» [math]\displaystyle{ 0\leqslant p \leqslant 1 }[/math] — вероятность «успеха» |
| Носитель | [math]\displaystyle{ k \in \{0,\dots,n\} }[/math] |
| Функция вероятности | [math]\displaystyle{ \binom{n}{k}\, p^k q^{n-k} }[/math] |
| Функция распределения | [math]\displaystyle{ I_{1-p}(n-\lfloor k\rfloor, 1+\lfloor k\rfloor) }[/math] |
| Математическое ожидание | [math]\displaystyle{ np }[/math] |
| Медиана | одно из [math]\displaystyle{ \{\lfloor np\rfloor-1, \lfloor np\rfloor, \lfloor np\rfloor+1\} }[/math] |
| Мода | [math]\displaystyle{ \lfloor (n+1)\,p\rfloor }[/math] |
| Дисперсия | [math]\displaystyle{ npq }[/math] |
| Коэффициент асимметрии | [math]\displaystyle{ \frac{q-p}{\sqrt{npq}} }[/math] |
| Коэффициент эксцесса | [math]\displaystyle{ \frac{1-6pq}{npq} }[/math] |
| Дифференциальная энтропия | [math]\displaystyle{ \frac12 \log_2 \big( 2\pi e\, np(1-p) \big) + O \left( \frac{1}{n} \right) }[/math] |
| Производящая функция моментов | [math]\displaystyle{ (q + pe^t)^n }[/math] |
| Характеристическая функция | [math]\displaystyle{ (q + pe^{it})^n }[/math] |
Биномиа́льное распределе́ние с параметрами [math]\displaystyle{ n }[/math] и [math]\displaystyle{ p }[/math] в теории вероятностей — распределение количества «успехов» в последовательности из [math]\displaystyle{ n }[/math] независимых случайных экспериментов, таких, что вероятность «успеха» в каждом из них постоянна и равна [math]\displaystyle{ p }[/math].
Определение
Пусть [math]\displaystyle{ X_1 ,\ldots, X_n }[/math] — конечная последовательность независимых случайных величин, имеющих одинаковое распределение Бернулли с параметром [math]\displaystyle{ p }[/math], то есть при каждом [math]\displaystyle{ i=1,\ldots, n }[/math] величина [math]\displaystyle{ X_i }[/math] принимает значения [math]\displaystyle{ 1 }[/math] («успех») и [math]\displaystyle{ 0 }[/math] («неудача») с вероятностями [math]\displaystyle{ p }[/math] и [math]\displaystyle{ q=1-p }[/math] соответственно. Тогда случайная величина
- [math]\displaystyle{ Y = X_1+X_2+ \ldots +X_n }[/math]
имеет биномиальное распределение с параметрами [math]\displaystyle{ n }[/math] и [math]\displaystyle{ p }[/math]. Это записывается в виде:
- [math]\displaystyle{ Y \sim \mathrm{Bin}(n,p) }[/math].
Случайную величину [math]\displaystyle{ Y }[/math] обычно интерпретируют как число успехов в серии из [math]\displaystyle{ n }[/math] одинаковых независимых испытаний Бернулли с вероятностью успеха [math]\displaystyle{ p }[/math] в каждом испытании.
Функция вероятности задаётся формулой:
- [math]\displaystyle{ p_Y(k) \equiv \mathbb{P}(Y = k) = \binom{n}{k}\, p^k q^{n-k}, \ \ k=0,\ldots, n, }[/math]
где
- [math]\displaystyle{ \binom{n}{k} = C_n^k = \frac{n!}{(n-k)! \, k!} }[/math] — биномиальный коэффициент.
Термин "биномиальный" используется так как [math]\displaystyle{ C_n^k = \binom{n}{k}\, p^k q^{n-k} }[/math] представляет собой [math]\displaystyle{ k }[/math]-й член биномиального разложения [math]\displaystyle{ (p+k)^n }[/math].
Функция распределения
Функция распределения биномиального распределения может быть записана в виде суммы:
- [math]\displaystyle{ F_Y(y) \equiv \mathbb{P}(Y \leqslant y) = \sum\limits_{k=0}^{\lfloor y \rfloor} \binom{n}{k}\, p^k q^{n-k},\; y \in\mathbb{R} }[/math],
где [math]\displaystyle{ \lfloor y \rfloor }[/math] обозначает наибольшее целое, не превосходящее число [math]\displaystyle{ y }[/math], или в виде неполной бета-функции:
- [math]\displaystyle{ F_Y(y) \equiv \mathbb{P}(Y \leqslant y ) = I_{1-p}(n-\lfloor y \rfloor,\lfloor y \rfloor +1) }[/math].
Максимальная вероятность в биномиальном распределении
Если в формуле [math]\displaystyle{ C_n^k = \binom{n}{k}\, p^k q^{n-k} }[/math] [math]\displaystyle{ k }[/math] изменяется от 0 до [math]\displaystyle{ n }[/math], то вероятность [math]\displaystyle{ C_n^k }[/math] сначала монотонно возрастает, а затем монотонно убывает, достигая своего наибольшего значения при [math]\displaystyle{ m=(n+1)p }[/math], за исключением случаев когда [math]\displaystyle{ C_n^{m-1}=C_n^m }[/math]. [math]\displaystyle{ C_n^m }[/math] - максимальная вероятность или наиболее вероятное число успехов. Однако, при большом количестве испытаний, то есть при большом [math]\displaystyle{ n }[/math], максимальная вероятность будет небольшой.
Моменты
Производящая функция моментов биномиального распределения имеет вид:
- [math]\displaystyle{ M_Y(t) = \left( pe^t + q\right)^n }[/math],
откуда
- [math]\displaystyle{ \mathbb{E}[Y] = np }[/math],
- [math]\displaystyle{ \mathbb{E}\left[Y^2\right] = np ( q + np ) }[/math],
а дисперсия случайной величины.
- [math]\displaystyle{ \mathbb{D}[Y] = npq }[/math].
Свойства биномиального распределения
- Пусть [math]\displaystyle{ Y_1 \sim \mathrm{Bin}(n,p) }[/math] и [math]\displaystyle{ Y_2 \sim \mathrm{Bin}(n, 1-p) }[/math]. Тогда [math]\displaystyle{ p_{Y_1}(k) = p_{Y_2}(n-k) }[/math].
- Пусть [math]\displaystyle{ Y_1 \sim \mathrm{Bin}(n_1,p) }[/math] и [math]\displaystyle{ Y_2 \sim \mathrm{Bin}(n_2,p) }[/math]. Тогда [math]\displaystyle{ Y_1 + Y_2 \sim \mathrm{Bin}(n_1+n_2, p) }[/math].
Связь с другими распределениями
- Если [math]\displaystyle{ n=1 }[/math], то получаем распределение Бернулли.
- Если [math]\displaystyle{ n }[/math] большое, то в силу центральной предельной теоремы [math]\displaystyle{ \mathrm{Bin}(n,p) \approx N( np, npq ) }[/math], где [math]\displaystyle{ N(np,npq) }[/math] — нормальное распределение с математическим ожиданием [math]\displaystyle{ np }[/math] и дисперсией [math]\displaystyle{ npq }[/math].
- Если [math]\displaystyle{ n }[/math] большое, а [math]\displaystyle{ \lambda }[/math] — фиксированное число, то [math]\displaystyle{ \mathrm{Bin}(n, \lambda / n) \approx \mathrm{P}(\lambda) }[/math], где [math]\displaystyle{ \mathrm{P}(\lambda) }[/math] — распределение Пуассона с параметром [math]\displaystyle{ \lambda }[/math].
- Если случайные величины [math]\displaystyle{ X }[/math] и [math]\displaystyle{ Y }[/math] имеют биномиальные распределения [math]\displaystyle{ \mathrm{Bin}(D,p) }[/math] и [math]\displaystyle{ \mathrm{Bin}(N-D,p) }[/math] соответственно, то условное распределение случайной величины [math]\displaystyle{ X }[/math] при условии [math]\displaystyle{ X+Y=n }[/math] – гипергеометрическое [math]\displaystyle{ \mathrm{HG}(D,N,n) }[/math].
См. также
В статье не хватает ссылок на источники (см. также рекомендации по поиску). |
