Интерференция в тонких плёнках

Интерференция отражённого света от поверхности мыльного пузыря

Интерфере́нция в тóнких плёнках — явление, которое возникает в результате разделения луча света при отражении от верхней и нижней границ тонкой плёнки. В результате возникают две световые волны, которые могут интерферировать. Тонкоплёночная интерференция объясняет цветовую палитру, видимую в свете, отражённом от мыльных пузырей и масляных плёнок на воде. Это явление также является основополагающим механизмом, используемым в объективах камер, зеркалах, оптических фильтрах и антибликовых покрытиях.

Теория

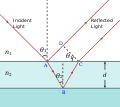
Луч света длиной волны [math]\displaystyle{ \lambda }[/math], распространяющийся в воздушной среде с показателем преломления [math]\displaystyle{ n_1=1 }[/math], при падении на поверхность плёнки с показателем преломления [math]\displaystyle{ n_2\gt n_1 }[/math] разделится на два луча. Часть отражается на верхней поверхности, а часть преломляется. Преломлённый луч достигает нижней границы, затем отражается от неё и, снова преломившись, выходит в воздушную среду когерентным с первым лучом. В силу условия когерентности двух лучей, наблюдается интерференционная картина, которая определяется оптической разностью хода между интерферирующими лучами:

[math]\displaystyle{ \Delta = L_2 - L_1 = n_2(OC+CB) - n_1(AO + \frac{\lambda_0}{2}) }[/math].

(1)

Интерференция в тонких плёнках

[math]\displaystyle{ \ \mathrm{OC} = \mathrm{CB} = \frac{d}{\cos(r)} }[/math]

[math]\displaystyle{ \ \mathrm{AO} = \mathrm{OB} \sin(i) }[/math]

[math]\displaystyle{ \ \mathrm{OB} = 2\cdot\mathrm{OK} = 2\mathrm{d}\cdot\operatorname{tg(r)} }[/math]

Учитывая закон преломления (закон Снеллиуса):

[math]\displaystyle{ \ \frac{\sin(i)}{\sin(r)} = \frac{n_2}{n_1} }[/math]

Получаем: [math]\displaystyle{ \ \sin(i) = n_2\cdot\sin(r) }[/math]

[math]\displaystyle{ \ \mathrm{AO} = \mathrm{OB}\cdot\sin(i) = 2\mathrm{d}\cdot\operatorname{tg(r)}\cdot\sin(i) = \frac{2d\cdot n_2\cdot\sin^2(r)}{\cos(r)} }[/math] Подставляем в [math]\displaystyle{ \ (1) }[/math]

[math]\displaystyle{ \Delta = 2d\sqrt{n^2-\sin^2i}-\frac{\lambda_0}{2} }[/math].[1]

Два луча дадут максимум, если [math]\displaystyle{ \Delta = \pm m \lambda_0 }[/math] и будет минимум, если [math]\displaystyle{ \Delta = \pm (2m + 1) \frac{\lambda_0}{2} }[/math]

Условие максимума интенсивности света при интерференции: [math]\displaystyle{ \ 2d\sqrt{n^2-\sin^2i}-\frac{\lambda_0}{2} = m\lambda_0 ; (m = 0, 1, 2...) }[/math]

Условие минимума интенсивности света при интерференции: [math]\displaystyle{ \ 2d\sqrt{n^2-\sin^2i}-\frac{\lambda_0}{2} =(2m + 1)\frac{\lambda_0}{2} ; (m = 0, 1, 2...) }[/math]

История

Интерференция на перьях павлина

Лазерный выходной соединитель покрыт множеством плёнок, уложенных друг на друга, для достижения отражательной способности 80 % при 550 нм. Слева: Зеркало обладает высокой отражающей способностью к жёлтому и зелёному цветам, но с высокой степенью пропускания к красному и синему. Справа: Зеркало пропускает 25 % лазерного излучения 589 нм.

Тонкоплёночная интерференция является обычно наблюдаемым явлением в природе, которое встречается у разных растений и животных. Одно из первых известных исследований этого феномена было проведено Робертом Гуком в 1665 году. Гук постулировал, что радуга в павлиньих перьях была вызвана тонкими чередующимися слоями пластины и воздуха [2].

В 1816 году Френель дополнил волновую теорию света. Тем не менее, очень мало было объяснений радуги до 1870-х годов, когда Джеймс Максвелл и Генрих Герц помогли объяснить электромагнитную природу света.

После изобретения интерферометра Фабри — Перо в 1899 году механизмы тонкоплёночных помех можно было продемонстрировать в более широком масштабе. Однако до начала XX века учёные объясняли радужный окрас у различных животных, например павлины и жуки-скарабеи, наличием красителей или пигментов, которые изменяют цвет при разных углах наблюдения.

В 1919 году лорд Рэлей предположил, что яркие, меняющиеся цвета были вызваны не красителями, а микроскопическими структурами, которые он назвал «структурными цветами» [3].

Первое производство тонкоплёночных покрытий произошло совершенно случайно. В 1817 году Йозеф Фраунгофер обнаружил, что потускнение стекла с азотной кислотой может уменьшить отражения на поверхности.

В 1819 году, наблюдая как слой спирта испаряется с листа стекла, Фраунгофер отметил, что цвета появились непосредственно перед тем, как жидкость полностью испарилась, и выяснилось, что любая тонкая плёнка из прозрачного материала будет создавать цвета.

Небольшое продвижение было сделано в технологии тонкоплёночного покрытия в 1936 году, когда Джон Стронг начал испарять флюорит, чтобы сделать антиотражающие покрытия на стекле.

В 1939 году Уолтер Х. Геффкен создал первые интерференционные фильтры с использованием диэлектрических покрытий.

Применение

В коммерческих проектах тонкие плёнки используются в антибликовых покрытиях, зеркалах и оптических фильтрах. Они могут быть спроектированы для контроля количества света, отражённого или прошедшего на поверхности для определённой длины волны.

Эллипсометрия — это метод, который часто используется для измерения свойств тонких плёнок. Поляризованный свет отражается от поверхности плёнки и измеряется детектором. Затем проводится модельный анализ, в котором эта информация используется для определения толщины слоя плёнки и показателей преломления. Двойная поляризационная интерферометрия является новым методом измерения показателя преломления и толщины тонких плёнок молекулярного масштаба.

Галерея

• 
  Яркая интерференционная картина наблюдается, когда свет отражается от верхней и нижней границ тонкой масляной пленки. Различные полосы образуются по мере уменьшения толщины плёнки от центральной точки стекания.
• 
  Цвета в свете отражаются от мыльного пузыря
• 
  Демонстрация разницы длины оптического пути для света, отражённого от верхней и нижней границ тонкой плёнки.
• 
  Тонкоплёночные помехи, вызванные размораживанием покрытия ITO на окне кабины Airbus.
• 
  Бензин на воде показывает образец ярких и тёмных полос при освещении лазерным светом 589 нм.
• 
  Конструктивное фазовое взаимодействие
• 
  Разрушительное фазовое взаимодействие
• 
  Интерференция в тонких плёнках в мыльном пузыре. Цвет зависит от толщины плёнки.
• 
  Падающий на мыльную плёнку свет в воздухе
• 
  Свет, падающий на масляную плёнку на воде
• 
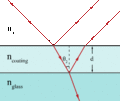
  Свет, падающий на антибликовое покрытие на стекле
• 
  Голубые пятна на крыльях бабочки Павлиний глаз обусловлены интерференцией в тонких плёнках.
• 
  Блеск цветов лютика обусловлен интерференцией в тонких плёнках.
• 
  Оптическое окно с антибликовым покрытием. Под углом 45° покрытие немного толще падающего света, в результате чего центральная длина волны смещается в сторону красного, и на фиолетовом конце спектра появляются отражения. При 0°, для которого было разработано это покрытие, отражения практически не наблюдается.
• 
  Закалка цветов происходит при нагреве стали и на поверхности образуется тонкая плёнка оксида железа. Цвет указывает на температуру, которую достигла сталь, что сделало это одним из самых ранних практических применений интерференции в тонких плёнках.
• 
  Радужные интерференционные цвета в масляной плёнке

См. также

• Интерференция волн
• Интерферометр
• Интерференция света

Литература

• Храмов Ю. А. Френель Огюстен Жан (Fresnel Augustin Jean) // Физики : Биографический справочник / Под ред. А. И. Ахиезера. — Изд. 2-е, испр. и доп. — М. : Наука, 1983. — С. 283. — 400 с. — 200 000 экз.
• Интерференция света / М. Д. Галанин // Большая советская энциклопедия : [в 30 т.] / гл. ред. А. М. Прохоров. — 3-е изд. — М. : Советская энциклопедия, 1969—1978.
• Тонкая плёнка и многослойная оптика вызывают структурную окраску многих насекомых и птиц. Materials today: Proceedings, 1S, 109—121 (2014).

Ссылки

• Stavenga, D. G.; Leertouwer, H. L.; Marshall, N. J.; Osorio, D. (2010) Изменения цвета у райской птицы, вызванные уникально структурированными бородками из перьев на груди
• Stavenga, D. G. (2014). Тонкая плёнка и многослойная оптика вызывают структурные цвета многих насекомых и птиц. Materials Today: Proceedings. 1: 109. doi:10.1016/j.matpr.2014.09.007