Интеграл Дарбу

Интеграл Дарбу — один из способов обобщения интеграла Римана на любые ограниченные на отрезке функции. Различают верхний и нижний интеграл Дарбу. Интегралы Дарбу геометрически представляют собой верхнюю и нижнюю площадь под графиком.

Определение

Для определения интегралов Дарбу прежде необходимо ввести вспомогательное понятие сумм Дарбу.

Нижняя (зеленая) и верхняя (серая) суммы Дарбу на 4 отрезках разбиения

Пусть на отрезке [math]\displaystyle{ [a,b] }[/math] определена функция вещественного переменного [math]\displaystyle{ f }[/math].

Разбиением [math]\displaystyle{ \tau }[/math] отрезка [math]\displaystyle{ [a,b] }[/math] будем называть конечное множество точек этого отрезка, включающего в себя точки [math]\displaystyle{ a }[/math] и [math]\displaystyle{ b }[/math]. Для удобства дальнейших записей будем вводить обозначения. Точки разбиения [math]\displaystyle{ \tau }[/math] обозначим за [math]\displaystyle{ x_i }[/math], причём пронумеруем их в порядке возрастания (начиная с нуля):

[math]\displaystyle{ \tau =\left\{ {{x}_{0}, \ldots {x}_{n}} \right\},\ a={{x}_{0}}\lt {{x}_{1}}\lt \ldots \lt {{x}_{n-1}}\lt {{x}_{n}}=b }[/math].

Множество всех разбиений отрезка [math]\displaystyle{ [a;b] }[/math] обозначим за [math]\displaystyle{ T }[/math].

Частичным отрезком разбиения [math]\displaystyle{ \Delta_i }[/math] назовём отрезок [math]\displaystyle{ [x_{i-1}, x_i] }[/math].

[math]\displaystyle{ \Delta_i=[x_{i-1}, x_i] }[/math]

Длину частичного отрезка разбиения обозначим за [math]\displaystyle{ \Delta x_i }[/math].

[math]\displaystyle{ \Delta x_i=x_i-x_{i-1} }[/math]

Диаметром разбиения [math]\displaystyle{ d }[/math] назовём максимальную длину частичного отрезка разбиения [math]\displaystyle{ \Delta x_i }[/math].

[math]\displaystyle{ d=\max \Delta x_i }[/math]

Точные грани функции на частичных отрезках разбиения обозначим за [math]\displaystyle{ m_i }[/math] и [math]\displaystyle{ M_i }[/math].

[math]\displaystyle{ {{m}_{i}}=\inf_{x \in \Delta_i} f(x) }[/math],

[math]\displaystyle{ {{M}_{i}}=\sup_{x \in \Delta_i} f(x) }[/math].

Тогда, нижней суммой Дарбу [math]\displaystyle{ s(f, \tau) }[/math] функции [math]\displaystyle{ f }[/math] на разбиении [math]\displaystyle{ \tau }[/math] называется

[math]\displaystyle{ s(f,\tau) = \sum_{i=1}^n m_i \Delta x_i }[/math]

Верхней суммой Дарбу [math]\displaystyle{ S(f, \tau) }[/math] называется

[math]\displaystyle{ S(f,\tau) = \sum_{i=1}^n M_i \Delta x_i }[/math]

Тогда нижним интегралом Дарбу [math]\displaystyle{ I_* }[/math] называется

[math]\displaystyle{ I_*=\sup_{\tau \in T} s(f,\tau) }[/math]

Верхним интегралом Дарбу [math]\displaystyle{ I^* }[/math] называется

[math]\displaystyle{ I^*=\inf_{\tau \in T} S(f,\tau) }[/math]

Альтернативные определения

Существуют также альтернативные определения интегралов Дарбу. Обычно они доказываются как свойства.

• Нижний интеграл Дарбу есть предел нижних сумм Дарбу при стремлении диаметра разбиения к нулю, а верхний есть предел верхних.

[math]\displaystyle{ I_* = \lim_{d(\tau) \to 0} s(f,\tau) }[/math]

[math]\displaystyle{ I^* = \lim_{d(\tau) \to 0} S(f,\tau) }[/math]

• Нижний интеграл Дарбу есть нижний предел интегральных сумм при стремлении диаметра разбиения к нулю, а верхний есть верхний предел.

[math]\displaystyle{ I_* = \varliminf_{d(\tau) \to 0} \sigma(f,\tau,\xi) }[/math]

[math]\displaystyle{ I^* = \varlimsup_{d(\tau) \to 0} \sigma(f,\tau,\xi) }[/math]

Свойства

Свойства сумм Дарбу

• При любых произвольно взятых двух разбиениях одного и того же отрезка, нижняя сумма Дарбу на одном разбиении не превосходит верхней суммы Дарбу на другом разбиении.

[math]\displaystyle{ \forall \tau_1, \tau_2 \in T \quad s(f,\tau_1)\le S( f,\tau_2) }[/math]

• Нижние суммы Дарбу ограничены сверху, а верхние — снизу.

Поведение нижней (зеленая) и верхней (серая) сумм Дарбу на измельчении разбиения

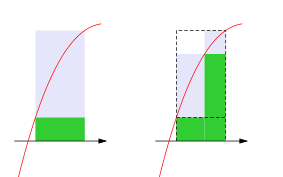
• При добавлении к имеющемуся разбиению новых точек нижняя сумма Дарбу никак не может уменьшиться, а верхняя никак не может увеличиться.

[math]\displaystyle{ \begin{align} s(f,\tau') \geq s(f,\tau)\\ S(f,\tau') \leq S(f,\tau) \end{align} \quad \tau' }[/math] — измельчение [math]\displaystyle{ \tau }[/math].

Более того, изменению этих сумм можно дать следующую оценку.

Пусть d — диаметр [math]\displaystyle{ \tau }[/math], измельчение [math]\displaystyle{ \tau' }[/math] — получено добавлением не более чем [math]\displaystyle{ l }[/math] точек к [math]\displaystyle{ \tau }[/math], [math]\displaystyle{ M }[/math] и [math]\displaystyle{ m }[/math] — точные грани функции [math]\displaystyle{ f }[/math] на отрезке [math]\displaystyle{ [a;b] }[/math]. Тогда

[math]\displaystyle{ s(f,\tau')-s(f,\tau) \leq (M-m)ld }[/math]

[math]\displaystyle{ S(f,\tau)-S(f,\tau') \leq (M-m)ld }[/math]

• Пусть [math]\displaystyle{ \sigma(f, \tau, \xi) }[/math] — интегральная сумма. При любом произвольно взятом разбиении с отмеченными точками [math]\displaystyle{ (\tau,\xi) }[/math] верно следующее неравенство:

[math]\displaystyle{ s(f,\tau) \leq \sigma(f,\tau,\xi) \leq S(f,\tau) }[/math]

• Суммы Дарбу есть точные грани интегральных сумм на данном разбиении. Пусть [math]\displaystyle{ \Xi }[/math] — множество всех возможных отмеченных точек на разбиении [math]\displaystyle{ \tau }[/math]. Тогда

[math]\displaystyle{ s(f, \tau) = \inf_{\xi \in \Xi} \sigma(f, \tau, \xi) }[/math],

[math]\displaystyle{ S(f, \tau) = \sup_{\xi \in \Xi} \sigma(f, \tau, \xi) }[/math].

Свойства интегралов Дарбу

• Для любой ограниченной на отрезке функции интегралы Дарбу существуют и конечны. Для неограниченной сверху функции верхний интеграл равен [math]\displaystyle{ +\infty }[/math], для неограниченной снизу нижний интеграл равен [math]\displaystyle{ -\infty }[/math].
• Для сумм и интегралов верны следующие неравенства

[math]\displaystyle{ s(f,\tau) \leq I_* \leq I^* \leq S(f,\tau) }[/math]

• Основная лемма Дарбу. Предел нижних сумм Дарбу при стремлении диаметра разбиения к нулю существует для любой ограниченной функции и равен нижнему интегралу Дарбу. Предел верхних сумм Дарбу при стремлении диаметра разбиения к нулю существует для любой ограниченной функции существует и равен верхнему интегралу Дарбу.

[math]\displaystyle{ \exists\lim_{d(\tau) \to 0}s(f, \tau) }[/math] и [math]\displaystyle{ I_* = \lim_{d(\tau) \to 0} s(f,\tau) }[/math]

[math]\displaystyle{ \exists\lim_{d(\tau) \to 0}S(f, \tau) }[/math] и [math]\displaystyle{ I^* = \lim_{d(\tau) \to 0} S(f,\tau) }[/math]

Основная лемма Дарбу устанавливает эквивалентность первого и второго определения интегралов Дарбу.

• Критерий Дарбу. Интегрируемость по Риману на [math]\displaystyle{ [a;b] }[/math] ограниченной на этом отрезке функции [math]\displaystyle{ f }[/math] равносильна равенству верхнего и нижнего интегралов Дарбу на этом отрезке.

[math]\displaystyle{ f }[/math] — интегрируема по Риману [math]\displaystyle{ \Leftrightarrow I_*=I^* }[/math]

Вариации и обобщения

Кратный интеграл Дарбу

По аналогии с кратным интегралом Римана можно определить и кратный интеграл Дарбу. Пусть [math]\displaystyle{ G }[/math] — измеримое по Жордану множество, [math]\displaystyle{ \tau }[/math] — его разбиение конечным числом измеримых по Жордану множеств. Обозначим множества этого разбиения за [math]\displaystyle{ \Delta_i }[/math].

[math]\displaystyle{ \tau =\left\{ {{\Delta}_{1}, \ldots {\Delta}_{n}} \right\} }[/math]

За [math]\displaystyle{ \Delta x_i }[/math] обозначим меру Жордана [math]\displaystyle{ \Delta_i }[/math].

Множество всех разбиений [math]\displaystyle{ G }[/math] будем обозначать [math]\displaystyle{ T }[/math].

Диаметр разбиения [math]\displaystyle{ d }[/math] определим как максимум из диаметров множеств разбиения (диаметр множества разбиения — точная верхняя грань расстояний между его точками).

[math]\displaystyle{ \max_{i=1}^n \sup_{x,y \in \Delta_i} |x-y| }[/math]

Точные грани функции на множествах разбиения обозначим за [math]\displaystyle{ m_i }[/math] и [math]\displaystyle{ M_i }[/math].

[math]\displaystyle{ {{m}_{i}}=\inf_{x \in \Delta_i} f(x) }[/math],

[math]\displaystyle{ {{M}_{i}}=\sup_{x \in \Delta_i} f(x) }[/math].

Тогда, нижней суммой Дарбу [math]\displaystyle{ s(f, \tau) }[/math] функции [math]\displaystyle{ f }[/math] на разбиении [math]\displaystyle{ \tau }[/math] называется

[math]\displaystyle{ s(f,\tau) = \sum_{i=1}^n m_i \Delta x_i }[/math]

Верхней суммой Дарбу [math]\displaystyle{ S(f, \tau) }[/math] называется

[math]\displaystyle{ S(f,\tau) = \sum_{i=1}^n M_i \Delta x_i }[/math]

Тогда нижним интегралом Дарбу [math]\displaystyle{ I_* }[/math] называется

[math]\displaystyle{ I_*=\sup_{\tau \in T} s(f,\tau) }[/math]

Верхним интегралом Дарбу [math]\displaystyle{ I^* }[/math] называется

[math]\displaystyle{ I^*=\inf_{\tau \in T} S(f,\tau) }[/math]

Все вышеперечисленные свойства сумм Дарбу и интегралов Дарбу, а также альтернативные определения сохраняются.

Литература

• Ильин В. А., Садовничий В. А., Сендов Бл. Х. Математический анализ. Начальный курс. — 2-е изд., перераб.. — М.: МГУ, 1985. — 662 с. с.
• Архипов Г. И., Садовничий В. А., Чубариков В. Н. Лекции по математическому анализу: Учебник для университетов и пед. вузов. — М.: Высшая школа, 1999. — 695 с. с. — ISBN 5-06-003596-4.
• Кудрявцев Л. Д. Курс математического анализа. В 3-х томах. Том 1. Дифференциальное и интегральное исчисления функций многих переменных (рус.). — М.: Дрофа, 2003. — 704 p.